Ανδρέας Ιωάννου Κασσέτας

Η σανίδα του Ιταλού

ΓΑΛΙΛΑΙΟΣ . Το κρίσιμο πειραμα

ΙΔΕΕΣ και ΑΝΤΙΚΕΙΜΕΝΑ.

Το έργο Φυσική άρχισε με την μακρόστενη σανίδα του Ιταλού και με την καινοτόμο τότε ιδέα του για τον ρόλο του ΧΡΟΝΟΥ κατά την εξέλιξη των πραγμάτων.

Η σανίδα ξύλινη, μακρόστενη,

επτά περίπου μέτρα

και με ένα αυλάκι ώστε να κυλάει

μια μικρή αλλά βαριά μπίλια από ορείχαλκο.

Κεκλιμένο επίπεδο είναι

ο όρος που θα επικρατήσει αργότερα.

Ο Ιταλός , εκείνη την εποχή 40 ετών,

ήταν βέβαια ο Galileo Galilei.

Η ΙΔΕΑ για τον ρόλο του χρόνου σημάδεψε τα όσα ακολούθησαν στη Φυσική.

Γιατί ο χρόνος τρέχει χύμα

κι εμείς δίνουμε ένα ΣΧΗΜΑ

Διονύσης Σαββόπουλος

Και ο χρόνος μπορεί να τρέχει χύμα, όπως λέει ο Έλληνας ποιητής,

αλλά ο Γαλιλαίος του έδωσε τη μορφή ποσότητας

και τον μέτρησε με ζυγαριά.

Το φαινόμενο

Στην άκρη του νήματος βρίσκεται η ΠΡΟΘΕΣΗ του να ερευνήσει το φαινόμενο πτώση κάθε σώματος προς το έδαφος. Μπορούσε εύκολα να διαπιστώνει το «εάν μια πέτρα βιάζεται να φθάσει στο έδαφος περισσότερο από μια σιδερένια μπάλα» αλλά εκείνος σκέφτηκε να ερευνήσει τη ΜΟΡΦΗ της κατακόρυφης αυτής κίνησης για κάθε αντικείμενο και η ιδέα «να μετρά τον χρόνο» έκανε την εμφάνισή της.

Η πτώση όμως ήταν και είναι μια κίνηση τρομακτικά «βιαστική». Οποιαδήποτε πέτρα αφήσει κανείς από το χέρι του, ακόμα κι αν το ύψος είναι δύο μέτρα, «εκείνη» θα προσγειωθεί στο έδαφος σε έξι δέκατα του δευτερολέπτου. Με ποιο τρόπο θα μπορούσε εκείνος να ερευνήσει το «πώς εξελίσσεται μέσα στον ελάχιστο αυτό χρόνο» το φαινόμενο ; Μπορούσε βέβαια να διακρίνει άμεσα, βασιζόμενος στην όραση, ότι, καθώς το σώμα κινείται βιαστικά προς το έδαφος, η θέση του αλλάζει, όπως επίσης το ότι αυξάνεται και ο ρυθμός μεταβολής της θέσης – πρώτη παράγωγο της θέσης θα το λένε αργότερα οι μαθηματικοί, οι φυσικοί το λένε ταχύτητα – ήταν όμως το ακόμα πιο δύσκολο ερώτημα «τι συμβαίνει, σε κάθε χρονική στιγμή, με τον χρονικό ρυθμό μεταβολής της ταχύτητας – δεύτερη παράγωγο της θέσης θα το λένε μετά από έναν αιώνα οι μαθηματικοί, εκείνος το είπε επιτάχυνση. Μήπως το μυστικό της πτώσης ήταν ότι κατά την εξέλιξή της, ο ρυθμός αυτός είναι χρονικά αναλλοίωτος ή μήπως έπρεπε να ελέγξει τον ρυθμό μεταβολής του ρυθμού μεταβολής της ταχύτητας – τρίτη παράγωγο της θέσης το λένε σήμερα οι μαθηματικοί . Ή μήπως κάτι ακόμα πιο σύνθετο ;

Το να ερευνήσει τέτοιες εξελίξεις μέσα σε λιγότερο από ένα δευτερόλεπτο, χωρις να διαθέτει κάποιο χρονόμετρο ήταν στα όρια του ανέφικτου. Μπροστά στο κατ’ αρχήν ανέφικτο η σκέψη του Γαλιλαίου λειτούργησε εντυπωσιακά.

Τα μεγάλα ΠΡΟΒΛΗΜΑΤΑ πριν από το πείραμα

Το πρώτο μεγάλο πρόβλημα ήταν η εδραιωμένη πεποίθηση

ότι ο ρυθμός πτώσης κάθε σώματος είναι ανάλογος προς το βάρος του

Το πρόβλημα ήταν δύσκολο να αντιμετωπιστεί διότι η άποψη αυτή με βασικό της στήριγμα το ότι είχε διατυωπωθεί από τον Αριστοτέλη είχε αποκρυσταλλωθεί σε ένα είδος «αλήθειας»

Την αντιμετώπισε, δείχνοντας, μέσα από ένα συλλογισμό, ότι η συγκεκριμένη άποψη ήταν ΑΝΤΙΦΑΤΙΚΗ.

Υποθέτουμε ότι η βαρύτερη πέτρα είναι Β και μόνη της πέφτει με V, ενώ η λιγότερο βαριά είναι β και μόνη της πέφτει με υ. Εάν τις συνδέσουμε – δημιουργώντας ένα ακόμα βαρύτερο σώμα - ώστε να πέσουν μαζί , έτσω με ταχύτητα υ’ , το β θα έπρεπε να επιβραδύνει το Β, ενώ το Β θα έπρεπε να κάνει το β να πέφτει πιο γρήγορα. Με σύμβολα υ < υ’ < V. Ωστόσο το Β+β σώμα που δημιουργήθηκε είναι βαρύτερο από το Β και θα έπρεπε να πέφτει πιο γρήγορα από ότι το Β μόνο του. Με σύμβολα υ’ > V

Ο συλλογισμός οδηγεί σε ασυνέπεια και η μόνος τρόπος για να αποφευχθεί είναι να ισχύει υ = υ’ = V.

Ο συλλογισμός έδειχνε βάσιμος αλλά δεν αρκούσε για να ανατρέψει την εδραιωμένη αλήθεια. Ο Γαλιλαίος κατανόησε ότι όφειλε να ερευνήσει την εξέλιξη του φαινομένου από στιγμή σε στιγμή.

Το δεύτερο μεγάλο πρόβλημα ήταν το αστραπιαίο της πτώσης .

Το αντιμετώπισε με την ιδέα « κεκλιμένη σανίδα επτά μέτρων, αυλάκι και μπίλια» σε μια κίνηση την οποία θεώρησε ΙΔΙΑΣ ΜΟΡΦΗΣ με την ελεύθερη πτώση . Εάν μπορούσε να διακρίνει κάτι σε αυτή την κίνηση και αυτό το κάτι ίσχυε για οποιαδήποτε γωνία κλίσης, η λογική του τον έπειθε ότι θα ίσχυε και για κλίση 90 μοιρών δηλαδή για κατακόρυφη κίνηση. Με την κεκλιμένη όμως σανίδα η κίνηση μιας μπίλιας δεν θα είχε το «αστραπιαίο μιας κατακόρυφης πτώσης», η σανίδα θα προκαλούσε μια πολύ πιο αργή κίνηση . Με σημερινές μετρήσεις ξέρουμε ότι για μια διαδρομή 6 μέτρων, εάν η κλίση της σανίδας είναι 20 μοίρες, ο χρόνος είναι κάτι λιγότερο από 2 δευτερόλεπτα, ενώ για 8 μοίρες είναι 3 περίπου δευτερόλεπτα.

Τέσσερεις περίπου δεκαετίες αργοτερα θα καταγράψει και θα δημοσιεύσει την εμπειρία, - Discorsi e dimostrazioni matematiche intorno a due nuove scienze, 1638, Leynden- γράφοντας στα ιταλικά :

Χρησιμοποιήσαμε μια ξύλινη σανίδα που είχε μήκος δώδεκα περίπου πήχεις , πλάτος μισό πήχυ και πάχος τρία δάκτυλα. Στην ακμή της ανοίχτηκε ένα αυλάκι με πλάτος λίγο μεγαλύτερο από ένα δάκτυλο. Αφού κάναμε αυτό το αυλάκι πολύ ίσιο, λείο και γυαλιστερό και το στρώσαμε με περγαμηνή, επίσης όσο πιο λεία και ομαλή γινόταν, αφήσαμε να κυλήσει μέσα του μια σκληρή λεία και πολύ στρογγυλή ορειχάλκινη μπάλα.

Το τρίτο πρόβλημα ήταν η μέτρηση του χρόνου.

Ακόμα όμως και στη κεκλιμένη σανίδα με το αυλάκι, η μπίλια κατέβαινε γρήγορα και τα χρονικά διαστήματα έπρεπε να μετρηθούν. Το αντιμετώπισε με την ιδέα «μέτρηση ποσοτήτων νερού» .

Γράφει στο Discorsi :

Χρησιμοποιήσαμε ένα μεγάλο δοχείο με νερό τοποθετημένο ψηλά. Στον πυθμένα του κολλήσαμε ένα σωλήνα μικρής διαμέτρου που έδινε μια λεπτή ροή νερού, το οποίο μαζεύαμε σε ένα άλλο δοχείο στη διάρκεια κάθε καθόδου, είτε για ολόκληρο το μήκος της διαδρομής είτε για ένα μέρος αυτού του μήκους . Το νερό που μαζεύαμε με αυτόν τον τρόπο το ζυγίζαμε μετά από κάθε κάθοδο με μια ζυγαριά πολύ μεγάλης ακριβείας . Οι διαφορές και οι αναλογίες αυτών των βαρών μας έδιναν τις διαφορές και τις αναλογίες των χρόνων και αυτό με τέτοια ακρίβεια, ώστε αν και οι δοκιμές επαναλήφθηκαν αν και τις δοκιμές τις επαναλάβαμε πολλές, πολλές φορές, δεν υπήρχε αισθητή διαφορά στα αποτελέσματα.

Πόσο ήταν άραγε το νερό που έτρεχε σε κάθε μονάδα χρόνου ; Το 2005, ο Manuel Lozano Leyva - Μανουέλ Λοθάνο Λέιβα- το υπολόγισε σε 1440 ml σε κάθε δευτερόλεπτο.

Γράφει ότι μέτρησε τον χρόνο με ζυγαριά. Ιδιαίτερα επινοητικό για να είναι αλήθεια και στα μέσα του 20^ου αιώνα αμφισβητήθηκε. Το 1953 ο Alexandre Koyré, ένας από τους σημαντικότερους ερευνητές του έργου του, υποστήριξε ότι ο Γαλιλαίος, προκειμένου να περιγράψει τον νόμο που είχε ανακαλύψει μέσα από τα συλλογισμούς και μαθηματικά, έγραφε για ένα πείραμα που δεν έγινε ποτέ. Ωστόσο, είκοσι περίπου χρόνια αργότερα, ο Stillman Drake, o σημαντικότερος ερευνητής της επόμενης γενιάς, ερευνώντας με τρομακτική υπομονή, στη Φλωρεντία, τα χειρόγραφα της Εθνικής Βιβλιοθήκης ανακάλυψε αδημοσίευτες σημειώσεις του ίδιου του Γαλιλαίου, σελίδες από το σημειωματάριό του, που καταδεικνύουν ότι πειράματα σαν αυτό που περιγράφει πρέπει να έγιναν στη Πάντοβα γύρω στο 1604.

Η Φυσική και η Μουσική . Σε ένα παλιό του άρθρο – The Role of Mousic in Galileo’ s Experiment , Scientific American , 232, 1975- ο Drake υποστηριζει ότι ο Γαλιλαίος, γιος μουσικού αλλά και γνώστης της μουσικής, διέθετε την ικανότητα που έχει ενός μαέστρος κινώντας την μπαγκέτα του να διαιρεί τον χρόνο σε ισα διαστήματα χωρίς να σκέφτεται τα δευτερόλεπτα. Με βάση αυτό, υποθέτει ότι ο Γαλιλαίος πριν αφήσει τη μπίλια να κυλήσει στο κεκλιμένο επίπεδο κρατούσε έναν ρυθμό τραγουδώντας έναν απλό σκοπό. Πιστεύει ότι, αφού ανακάλυψε το «μυστικό», προχώρησε στις μετρήσεις με το υδροχρονόμετρο τις οποίες περιγράφει στο Discorsi.

Το τέταρτο πρόβλημα ήταν οι λογικές διεργασίες που θα οδηγούσαν από τα δεδομένα στη διατύπωση κάποιου νόμου

Μετά από επανειλημμένες προσπάθειες, τα δεδομένα– αποστάσεις μετρημένες με χάρακα και αντίστοιχα χρονικά διαστήματα - ήταν πλέον μπροστά του και έπρεπε με τη σκέψη του να τα επεξεργαστεί.

Ο Drake υποστηρίζει ότι αυτό που περιγράφει Discorsi είναι μια πειραματική επίδειξη η οποία επιβεβαιώνει τον νόμο και όχι οι προσπάθειες και οι δυσκολίες που αντιμετώπισε μέχρι να φθάσει εκεί. Ωστόσο μέσα από τα σημειωματάριά του αποκαλύπτονται οι δυσκολίες που αντιμετώπισε. Η «ανάκριση» στην οποία είχε υποβάλει τη Φύση – με ξύλινη σανίδα, ορειχάλκινες μπίλιες και νερό - ώστε να ομολογήσει το μυστικό της οποιασδήποτε πτώσης του είχε δώσει ποσότητες με αριθμούς και έπρεπε μέσα από τους αριθμούς – οι οποίοι δεν ήταν απόλυτα ακριβείς - να βρει τον δρόμο.

Στo πρώτο χρονικό διάστημα – ας το πούμε t, θεωρώντας το μονάδα χρόνου – η μπίλια είχε μετακινηθεί κατά 33 μονάδες μήκους – ας το συμβολίσουμε με 33d - σε διάστημα 2t είχε συνολικά καλύψει 130d, σε 3t, σύμφωνα με τις μετρήσεις του, 298 d και σε χρονικό διάστημα 4t είχε μετακινηθεί κατά 526d . Τι σχέση μπορούσε να έχει το 33, το 130, το 298 και το 526 ;

Ο Γαλιλαίος «έπαιξε» με διάφορους τρόπους τόσο με αυτούς τους αριθμούς όσο και με τα διαστήματα που φαινόταν να καλύπτει η μπίλια κατά τη διάρκεια κάθε διαδοχικής μονάδας χρόνου μέχρι να διακρίνει ότι, σύμφωνα με την Αριθμητική, το 130 είναι 3,93 φορές μεγαλύτερο από το 33, ότι το 298 είναι 9,03 φορές μεγαλύτερο από το 33 και ότι 526 = 15,93 . 33 . Τελικά στρογγυλοποίησε τους αριθμούς, στο σημειωματάριό του, και, χρησιμοποιώντας διαφορετικο μελάνι και πένα έγραψε σε μια στήλη τους ακέραιους . Στη θέση του 3,93 έγραψε 4 και στη θέση του 9,03 έγραψε τον ακέραιο 9 και στη θέση του 15,94 έγραψε τον ακέραιο 16. Αποδεχόμενος κάποια σφάλματα στις μετρήσεις, είχε βρει το κλειδί.

Η απόσταση της μπίλιας από το σημείο που κάθε φορά αφηνόταν ήταν ανάλογη με το τετράγωνο του αντίστοιχου χρόνου.

Ο George Johnson στο The Ten most Beautiful Experriments ( 2008) γράφει :

That Galileo’ s numbers were not exact testified to the reality of the experiment. That they were as close as they were testified to his skills as an experimenter.

Το ότι οι αριθμοί του Γαλιλαίου δεν ήταν ακριβείς καταδεικνύει ότι το πείραμα είχε πραγματοποιηθεί.

Το ότι ήταν τόσο κοντά στις ακριβείς τιμές καταδεικνύει τις δεξιότητές του ως πειραματιστή.

Τα μετά από το πείραμα

Οι έννοιες .

Η εμπειρία οδήγησε και σε μια ακόμα ΙΔΕΑ από την οποία «γεννήθηκε» μια καινούρια έννοια . Η ιδέα ήταν ότι «ένα αντικείμενο, θα μπορούσε, κατά την κίνησή του, να έχει, σε κάθε στιγμή, μια διαφορετική ταχύτητα και ότι θα μπορούσαμε να προτείνουμε μια καινούρια ΕΝΝΟΙΑ ικανή να περιγράφει τις αλλαγές της ταχύτητάς του».

Ο Γαλιλαίος αρχικά σκέφτηκε ότι η καινούρια έννοια θα μπορούσε να περιγράφει το «πόσο αυξάνεται η ταχύτητα σε κάθε μονάδα μετατόπισης» αλλά τελικά κατέληξε στην επιλογή η καινούρια έννοια να περιγράφει το «πόσο αυξάνεται η ταχύτητα σε κάθε μονάδα χρόνου ». Η καινούρια ΕΝΝΟΙΑ θα πάρει το όνομα ΕΠΙΤΑΧΥΝΣΗ, αν και στα χρόνια που ακολούθησαν η έννοια διαμορφώθηκε σε κάτι ευρύτερο.

Η εμπειρία «διαστήματα ανάλογα με τα τετράγωνα των χρόνων» μπορούσε πλέον να περιγραφεί και με την έννοια επιτάχυνση και να διατυπωθεί με το «κατά την εξέλιξη της κίνησης η επιτάχυνση διατηρείται σταθερή».

Επαναλαμβάνοντας τους πειραματισμούς με άλλη μπίλια και με διαφορετικές γωνίες της σανίδας με το έδαφος διαπίστωνε πως όταν μεγάλωνε τη γωνία η μπίλια κατηφόριζε πιο γρήγορα, όσο ανύψωνε τη σανίδα η επιτάχυνση γινόταν μεγαλύτερη αλλά κατά την εξέλιξη της κίνησης σταθερή και ότι ο κανόνας «διαστήματα ανάλογα με το τετράγωνο του χρόνου» ήταν πάντα ίδιος .

Οι νόμοι

1. Ο νόμος για την πτώση

Ο «κανόνας» έδειχνε να ισχύει για ΚΑΘΕ γωνία, άρα «λογικά» έπρεπε να ισχύει ακόμα κι αν η γωνία της σανιδας με το οριζόντιο έδαφος γινόταν γωνία ενενήντα μοιρών. Ο κανόνας έπρεπε να ισχύει ακόμα κι αν η μπίλια έπεφτε κατακόρυφα. Υποστήριξε γενικεύοντας ότι πρόκειται για έναν ΝΟΜΟ της φύσηςη .

ΚΑΤΑ ΤΗΝ ΠΤΩΣΗ ΟΠΟΙΟΥΔΗΠΟΤΕ ΣΩΜΑΤΟΣ τα διαστήματα είναι ανάλογα με τα τετράγωνα των αντίστοιχων χρόνων . Κατά τη διάρκεια της πτώσης η επιτάχυνση είναι σταθερή

Στην παγκόσμια γλώσσα των φυσικών η επιτάχυνση της ελεύθερης τώσης συμβολίζεται προς τιμήν με το γράμμα g , αρχικό του ονόματός του.

Στην ελληνική σημειολογική παράδοση η έννοια επιτάχυνση, για έναν αιώνα περίπου – μέχρι το 1984 –, συμβολιζόταν με το ελληνικό γράμμα γ.

Αν και δεν έχει γίνει σχετική ιστορική έρευνα που να το βεβαιώνει,

η προσωπική μου άποψή για την ελληνική αυτή επιλογή είναι ότι το γ είναι το ελληνικό αρχικό του ονόματος Γαλιλαίος .

2. Ο νόμος της αδράνειας

Η εμπειρία, δίδασκε επίσης ότι όσο μίκραινε τη γωνία της σανίδας με το οριζόντιο έδαφος η επιτάχυνση γινόταν όλο και μικρότερη και οδηγούσε τη σκέψη προς την ιδέα ότι εάν η σανίδα γινόταν οριζόντια - και το σώμα είχε ήδη ταχύτητα - η κίνηση θα γινόταν με επιτάχυνση μηδέν. Η σχετική εμπειρία με τη σανίδα είχε δείξει εξάλλου πώς όταν η μπίλια διέσχιζε όλο το αυλάκι, συνέχιζε τη διαδρομή της στην οριζόντια επιφάνεια του πατώματος με μηδενική επιτάχυνση .

Η ιδέα ήταν – ιδιαίτερα εικονοκλαστική σε σχέση με τα ισχύοντα – ήταν ότι η μπίλια κάποτε σταματούσε επειδή στο πάτωμα υπάρχει τριβή και ότι σε οριζόντιο έδαφος χωρίς τριβή η μπίλια θα συνέχιζε να κινείται ίσια με μηδενική επιτάχυνση, χωρίς η κίνησή της να χρειάζεται την οποιαδήποτε «βοήθεια» ώστε να διατηρείται αναλλοίωτη.

Ο Γαλιλαίος είχε οδηγηθεί στον νόμο της αδράνειας.

Από τα γνωστά κείμενα δεν απορρέει είναι σαφές αν «η χωρίς δυναμεις αυτή κίνηση» είναι μια ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ή μια κίνηση πάνω σε κύκλο παράλληλο προς την επιφάνεια της Γης. Σε ορισμένα κείμενα διακρίνει κανείς ότι η φυσική – αδρανειακή – κίνηση είναι γι αυτόν μια κίνηση που δεν κατευθύνεται ούτε προς τα πάνω ούτε προς τα κάτω, αλλά το αντικείμενο διατηρείται σε σταθερή αποσταση απο το κέντρο της Γης.

Τον νόμο της αδράνειας για ΕΥΘΥΓΡΑΜΜΗ κίνηση θα τον διατυπώσει ο Descartes – Καρτέσιος στο Αρχές της Φιλοσοφίας, το 1644, θα τον επαναφέρει δέκα χρόνια αργότερα ο Huygens και ο Newton - Νεύτων θα τον θεωρήσει πρώτο αξίωμα – νόμο της κίνησης, στο Principia, το 1686.

3. Η κίνηση των βλημάτων και ο Απολλώνιος.

Βασιζόμενος στα παραπάνω και αξιοποιώντας μια ακόμα δική του ΙΔΕΑ,

οδηγήθηκε στο να ερευνήσει την κίνηση κάθε σώματος το οποίο εκτοξεύεται.

Η ΙΔΕΑ ήταν ότι η κίνηση ενός σώματος μπορεί μπορεί να αναλύεται σε δύο ταυτοχρονες και ανεξάρτητες μεταξύ τους κινήσεις.

Η θεωρητική επεξεργασία τον οδήγησε στη διαπίστωση ότι

η τροχιά κάθε σώματος που εκτοξεύεται οριζόντια

είναι μια ΓΡΑΜΜΗ, σαν εκείνη που είχε εντοπίσει

ο Απολλώνιος ότι προκύπτει από την τομή ενός κώνου

από επίπεδο παράλληλο προς τη γενέτειρα. Το όνομα της, σύμφωνα με τον Απολλώνιο ΠΑΡΑΒΟΛΗ, για τον Γαλιλαίο ήταν parabola.

Στο Discorsi e dimostrazioni matematiche intorno a due nuove scienze γράφει :

Προτείνω τώρα να εκθέσουμε τις ιδιότητες που ταιριάζουν σε ένα σώμα του οποίου η κίνηση συντίθεται από δύο άλλες κινήσεις δηλαδή μια ομαλή και μια φυσικά επιταχυνόμενη. .

Ένα βλήμα το οποίο ωθείται από μια ομαλή οριζόντια κίνηση η οποία συνδυάζεται με μια επιταχυνόμενη κατακόρυφη κίνηση, διαγράφει τροχιά η οποία αποτελεί ημιπαραβολή

Δεδομένου ότι δεν διαθέτει ΑΝΑΛΥΤΙΚΗ ΓΕΩΜΕΤΡΙΑ, για να το αποδείξει, θα βασιστεί στις ιδιότητες της παραβολής όπως έχουν προταθεί από τον Απολλώνιο.

Γράφει στο Ημέρα Τρίτη του Discorsi :

Η βάση bc της παραβολής τέμνει κάθετα τη διάμετρο του κύκλου ibkc και ο άξονας ad είναι παράλληλος προς την πλευρά Ιk. Θεωρώ ένα τυχαίο σημείο f στo τμήμα της παραβολής bfa και φέρνω την fe παράλληλη προς την bd. Τότε λέγω ότι το τετράγωνο της bd έχει την ίδια αναλογία με το τετράγωνο της fe που έχει ο άξονας ad με το τμήμα ae.

(bd) ² /(fe) ² = (ad)/(ae) . 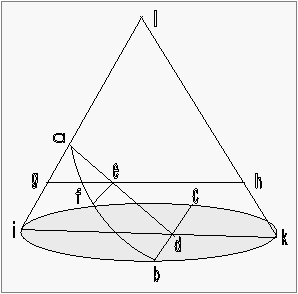Από το σημείο e διέρχεται ένα επίπεδο παράλληλο προς τον κύκλο ibkc, το οποίο ορίζει μέσα στον κώνο έναν κύκλο με διάμετρο την geh. Εφόσον η bd είναι κάθετη στην ik μέσα στον κύκλο ibkc το τετράγωνο της είναι ισοδύναμο με το ορθογώνιο που σχηματίζεται από τις id και dk . (bd) ² = (id).(dk) .

Επίσης στον άνω κυκλο που περνά από τα σημεία g, f, h το τετράγωνο της fe είναι ισοδύναμο με το ορθογώνιο που σχηματίζεται από τις ge και eh.

(fe) ² = (ge).(eh) . Γι αυτό το τετράγωνο της bd έχει με το τετράγωνο της fe την ίδια αναλογία που έχει και το ορθογώνιο (id)(dk) με το ορθογώνιο (ge)(eh) .

Και εφόσον το τμήμα ed είναι παράλληλο στην hk, το τμήμα eh που είναι παράλληλο στο dk είναι ίσο με αυτό. Επομένως, το ορθογώνιο (id)(dk) έχει με το ορθογώνιο (ge)(eh) την ίδια αναλογία που έχει το id με το ge , την ίδια δηλαδή που έχει το da με το ae, από όπου επίσης το ορθογώνιο (id)(dk) είναι με τον ίδιο τρόπο ανάλογο με το ορθογώνιο (ge)(eh), δηλαδή το τετράγωνο της (bd) έχει την ίδια αναλογία με το τετράγωνο της (fe), που έχει το τμημα (ad) με το τμήμα (ae)

Κατά την οριζόντια βολή, η κινηση του σώματος αναλύεται

σε μια οριζόντια ομαλή κίνηση

και σε μια κατακόρυφη με σταθερή επιτάχυνση.

Σε δύο τυχαίες χρονικές στιγμές t₁ και t₂

ο λόγος των οριζόντιων μετατοπίσεων

είναι ίσος με το λόγο των χρονικών διαστημάτων

x₁ /x₂ = t₁ /t₂ ,

ενώ ο λόγος των κατακόρυφων μετατοπίσεων

είναι ίσος με το λόγο των χρονικων διαστημάτων στο τετράγωνο

y₁ /y₂ = (t₁ /t₂)² . Αρα για δύο οποιαδήποτε σημεία της τροχιάς ισχύει y₁ /y₂ = (x₁ /x₂)² οπότε , σύμφωνα με την απόδειξη του Γαλιλαίου, - τα δύο τυχαία σημεία – άρα ΟΛΑ της σημεία της τροχιάς - ανήκουν σε μία ΠΑΡΑΒΟΛΗ .

Και δεν σταμάτησε εκεί . Η εμπειρία

ήταν πάντοτε το κριτήριο

για την επιβεβαίωση

ή τη διάψευση

των θεωρητικών του

συλλήψεων.

Διαθέτοντας μια θεωρία ικανή

να τον οδηγεί σε προβλέψεις για το

«που θα βρίσκεται μια μπίλια»

αν εκτοξευτεί με ορισμένη οριζόντια ταχύτητα, δοκίμασε να επιβεβαιώσει

τις προβλέψεις του στο εργαστήριο . Ξύλινες κατασκευές, μεταλλικοί δακτύλιοι, μπίλιες,

ήταν ΑΝΤΙΚΕΙΜΕΝΑ στα οποία πάντοτε θα επέστρεφε για να τεκμηριώσει τις θεωρητκές του συλλήψεις, διδάσκοντας τους μεταγενέστερους το πώς ακριβώς φαντάζεται ότι πρέπει να λειτουργεί η Νέα Επιστήμη.

ΑΝΤΙΚΕΙΜΕΝΑ

ΦΑΙΝΟΜΕΝΑ

ΓΕΩΜΕΤΡΙΑ

ΔΡΑΣΗ πάνω στα ΑΝΤΙΚΕΙΜΕΝΑ και

ΙΔΕΕΣ που θα οδηγούσαν σε ΕΝΝΟΙΕΣ και σε ΝΟΜΟΥΣ

.