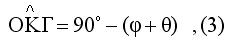Τριχοτόμηση  Γωνίας -Η  λύση  του  Νικομήδη
 
            Ο Νικομήδης για να λύση το πρόβλημα  της τριχοτόμησης της γωνίας και του τετραγωνισμού του κύβου επινόησε  μια καμπύλη ,την  κογχοειδή  την  οποία παρουσιάζουμε παρακάτω στο πρόβλημα του διπλασιασμού του κύβου -η λύση του Νικομήδη. Στο παρακάτω applet παρουσιάζουμε  την τριχοτόμηση της γωνίας χρησιμοποιώντας την κογχοειδή καμπύλη. Διαβάστε  τις οδηγίες
 
Αν διαβάζεται αυτό το κείμενο τότε δεν βλέπετε το applet και ο  Browser σας  δεν  έχει το Java 2 Runtime Environment .Δείτε τις οδηγίες στην αρχική σελίδα και κατεβάστε το

Νικομήδης, Έλληνας μαθηματικός του 2ου αι. .π.χ

Άνοιγμα του applet σε νέο παράθυρο

Για την απόδειξη ας  θέσουμε 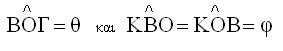     είναι ΚΒ=ΚΟ    ως  ακτίνες του κύκλου
Από το ορθογώνιο τρίγωνο  ΟΖΓ  έχουμε 

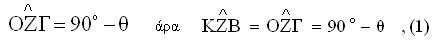Επειδή το σημείο Β ανήκει στη κογχοειδή  είναι ΒΖ=β=ΚΟ=ΚΒ  αφού η κογχοειδή γράφτηκε  με  διάστημα β=ΚΟ  άρα το τρίγωνο ΚΒΖ  είναι ισοσκελές και έχουμε   
                                                                         

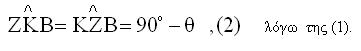Από το ορθογώνιο τρίγωνο ΚΓΟ  έχουμε       

Από τις  (2)  ,(3) με πρόσθεση  προκύπτει      
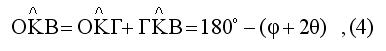Από το ισοσκελές τρίγωνο  ΟΚΒ  έχουμε          Από τις  (4),(5)  προκύπτει         
                                                          
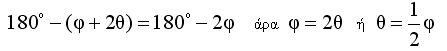  δηλ 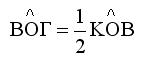                                   Έτσι  η γωνία  ΧΟΖ  τριχοτομήθηκε .
Βιβλιογραφία

Κεντρική σελίδα  

 

Η λύση του : Αρχιμήδη-1, Αρχιμήδη-2, Πάππου -1, Πάππου -2 , Ιππία, Νικομήδη, Pascal

                     Μηχανικοί τριχοτόμοι