Ο γενικός ορισμός του τηλεσκοπίου είναι: "Το τηλεσκόπιο είναι ένα όργανο για την θέαση απομακρυσμένων αντικειμένων". Οι περισσότεροι άνθρωποι πιστεύουν ότι το τηλεσκόπιο κυρίως μεγεθύνει, αλλά όσο περισσότερο μεγεθύνεις μια εικόνα σε ένα τηλεσκόπιο τόσο πιο σκοτεινή και θολή γίνεται η εικόνα. Έτσι, ένα τηλεσκόπιο για να είναι χρήσιμο θα πρέπει εκτός από τη μεγέθυνση να κρατά φωτεινή και να καθαρή την εικόνα.

Όλα τα οπτικά τηλεσκόπια θα πρέπει να πληρούν τις τρεις παρακάτω προϋποθέσεις: Να συγκεντρώνουν φως για να κρατούν φωτεινό το είδωλο, να δίνουν καθαρή εικόνα και να μεγεθύνουν. Κάθε μια από αυτές τις προϋποθέσεις εξαρτάται άμεσα από τη διάμετρο του αντικειμενικού φακού ή κατόπτρου. Ή πιο απλά, όσο μεγαλύτερη είναι η διάμετρος που έχει ο αντικειμενικός φακός ή κάτοπτρο του τηλεσκοπίου τόσο καλύτερα αυτό θα αποδίδει.

ΙΚΑΝΟΤΗΤΑ ΣΥΛΛΟΓΗΣ ΦΩΤΟΣ
(light gathering ability): Το τηλεσκόπιο λειτουργεί σαν χοάνη φωτός. Αν πάρετε όλο το φως που μπαίνει στο τηλεσκόπιο, δηλαδή το φως που πέφτει πάνω στον αντικειμενικό φακό ή κάτοπτρο και το συγκεντρώσετε σε μια μικρή εικόνα ώστε να χωρά μέσα από την κόρη του ματιού, τότε έχετε αυξήσει τη συγκέντρωση φωτός σ' αυτή τη μικρή περιοχή και η εικόνα είναι πολύ πιο φωτεινή. Αυτό γίνεται και σε ένα τηλεσκόπιο. Ο αντικειμενικός είναι κυρτός και συγκεντρώνει το φως φέρνοντας τις ακτίνες προς το κέντρο.

Για να υπολογίσετε την ικανότητα συλλογής φωτός ενός τηλεσκοπίου απλά εφαρμόστε τον τύπο:

Ικανότητα Συλλογής Φωτός = (Διάμετρος αντικειμενικού mm/ 7mm)^2

Σημείωση: η διάμετρος μετράται σε mm (1 ίντσα = 25,4mm).

Για παράδειγμα ας υπολογίσουμε την ικανότητα συλλογής φωτός πέντε τηλεσκοπίων με διαφορετική διάμετρο.

Η ικανότητα συλλογής φωτός εξαρτάται επίσης από τη διαδρομή του φωτός μέσα στο τηλεσκόπιο. Το φως στην πορεία του συναντά πολλά εμπόδια όπως δευτερεύοντα κάτοπτρα, στρώματα επικάλυψης και διαφράγματα που έχουν σημαντική επίπτωση στην ικανότητα συλλογής φωτός. Στην πραγματικότητα, για να αυξηθεί η ικανότητα συλλογής φωτός ενός τηλεσκοπίου θα πρέπει να αυξηθεί η διάμετρος του κυρίως φακού ή κατόπτρου.

ΓΩΝΙΑ ΔΙΑΚΡΙΣΗΣ (resolving power) ή διακριτική ικανότητα, είναι η δυνατότητα που έχει ένα τηλεσκόπιο να δίνει ευκρίνεια, δηλαδή να ξεχωρίζει το φως σε ανεξάρτητα φωτεινά σημεία. Π.χ. Την επόμενη φορά που θα ανεβείτε νύχτα σε αυτοκίνητο σε έναν επίπεδο και μακρύ δρόμο, προσέξτε ένα αυτοκίνητο που σας πλησιάζει από το αντίθετο ρεύμα. Αρχικά, σε μεγάλη απόσταση τα φώτα θα εμφανιστούν σαν ένα και καθώς έρχονται πιο κοντά αρχίζουν να διαχωρίζονται σε δύο δέσμες φωτός. Το παρακάτω σχήμα δείχνει πώς εμφανίζονται τα φώτα όταν το αυτοκίνητο είναι μακριά (σημείο Α) και πως όταν πλησιάζει (σημείο Γ). Βέβαια, ποτέ μην επιχειρήσετε να κάνετε αυτή τη δοκιμή στη θέση του οδηγού γιατί μπορεί να προκαλέσετε ατύχημα.

Το ίδιο ακριβώς συμβαίνει όταν παρατηρούμε τον ουρανό. Μπορεί να βλέπουμε μόνο ένα αστέρι με τα μάτια μας, αλλά μέσα από ένα τηλεσκόπιο βλέπουμε πλήθος άστρων λόγω της διακριτικής ικανότητας που έχει ένα τηλεσκόπιο. Με το γυμνό μάτι μπορούμε να διακρίνουμε αντικείμενα που απέχουν κατά προσέγγιση 6 λεπτά της μοίρας. Για να υπολογίσετε την γωνία διάκρισης ενός τηλεσκοπίου εφαρμόστε τον τύπο:

Γωνία διάκρισης (σε δευτερόλεπτα της μοίρας - arc seconds)
= 4,56 / Διάμετρος αντικειμενικού "σε ίντσες"
ή
= 4,56 * 25,4/Διάμετρος αντικειμενικού "σε mm"

Ας χρησιμοποιήσουμε τον τύπο για να υπολογίσουμε τη γωνία διάκρισης για κάποια τηλεσκόπια :

Έτσι, γνωρίζοντας την γωνία διάκρισης ενός τηλεσκοπίου και τη γωνία διαχωρισμού δύο αντικειμένων μπορούμε να πούμε αν είναι δυνατό αυτά να φαίνονται σαν ξεχωριστά αντικείμενα ή όχι. Το σχήμα που ακολουθεί δείχνει τη γωνία διάκρισης με γκρι χρώμα. Αν η γωνία αυτή μεταξύ δύο άστρων είναι ίση ή μεγαλύτερη από τη γωνία αυτή τότε θα βλέπουμε να απεικονίζονται δύο άστρα και αν όχι τα άστρα θα εμφανίζονται σαν ένα.

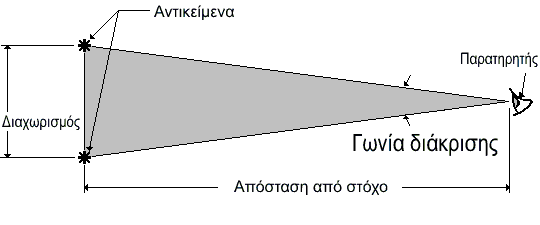Προσέξτε ότι ένα τηλεσκόπιο με μεγάλη διάμετρο μπορεί να διακρίνει καλύτερα τα αντικείμενα γιατί έχει μικρότερη γωνία διάκρισης.

ΜΕΓΕΘΥΝΣΗ: Η τρίτη παράμετρος ενός τηλεσκοπίου είναι η μεγέθυνση η οποία υλοποιείται στον προσοφθάλμιο και όχι στον αντικειμενικό φακό(ή κάτοπτρο). Ο αντικειμενικός παίρνει τις ακτίνες φωτός και τις συμπυκνώνει σε μια μικρή - φωτεινή και καθαρή εικόνα (σμίκρυνση). Ο προσοφθάλμιος κάνει ακριβώς το αντίθετο. Παίρνει την μικρή εικόνα και την μεγεθύνει ελαφρώς έτσι ώστε να χωρά στο μέγεθος της κόρης του ματιού.

Καθώς η εικόνα μεγαλώνει για να μπορέσουμε να τη δούμε, χάνουμε μέρος από την ανάλυση και τη φωτεινότητα γιατί ο προσοφθάλμιος λειτουργεί αντίστροφα από το τηλεσκόπιο. Ενώ το τηλεσκόπιο σμικρύνει την εικόνα του παίρνει με τον αντικειμενικό φακό, (το συγκεντρώνει σε μια μικρή περιοχή), ο προσοφθάλμιος μεγεθύνει ελαφρά την εικόνα. Φαίνεται παράλογο να σμικρύνεται και στη συνέχεια να μεγεθύνεται, αλλά αυτό είναι απαραίτητο ώστε να μπορούμε να εστιάζουμε και να επιλέγουμε διαφορετικές μεγεθύνσεις για κάθε αντικείμενο. Στην πραγματικότητα η μεγέθυνση της εικόνας είναι ένα πολύ μικρό ποσοστό σε σχέση με τη συνολική σμίκρυνση που επιτυγχάνει το τηλεσκόπιο.

Όταν μια εικόνα μεγεθύνεται είναι σαν να μεγαλώνουμε μια φωτογραφία. Η εικόνα είναι μεγαλύτερη αλλά ταυτόχρονα γίνεται σκοτεινή και θολή. Όσο πιο πολύ μεγεθύνεται μια εικόνα τα φωτεινά σημεία μιας εικόνας απομακρύνονται με αποτέλεσμα μια σκοτεινή εικόνα. Για αυτό τον λόγο οι αστρονόμοι χρησιμοποιούν τους δυο παρακάτω πρακτικούς κανόνες για τη μεγέθυνση.

Για παράδειγμα ας υπολογίσουμε τις μέγιστες και ελάχιστες τιμές πρακτικής μεγέθυνσης για μερικά τηλεσκόπια:

Κάνετε υπολογισμούς για το τηλεσκόπιο σας!

Επομένως αν δείτε ένα τηλεσκόπιο που να διαφημίζεται ότι έχει μεγέθυνση Χ400 έχοντας διάμετρο αντικειμενικού 2 ίντσες (~50mm) να είστε σίγουροι ότι δεν θα έχει καλή ποιότητα ειδώλου στην μεγέθυνση αυτή. Να θυμάστε τους δυο παραπάνω κανόνες πρακτικής μεγέθυνσης και ότι όσο περισσότερο μεγεθύνουμε τόσο περισσότερο μειώνεται η ποιότητα και η φωτεινότητα του ειδώλου.

Εκτός από τις παραπάνω σημαντικές παραμέτρους σε ένα τηλεσκόπιο, μια άλλη μικρότερης ίσως σημασίας παράμετρος ενός τηλεσκοπίου είναι ο :

ΕΣΤΙΑΚΟΣ ΛΟΓΟΣ

Ο εστιακός λόγος ενός τηλεσκοπίου είναι ο λόγος του εστιακού μήκους προς την διάμετρο. Όπου, εστιακό μήκος είναι η απόσταση από τον κύριο φακό (ή κάτοπτρο) ως το σημείο εστίασης. Για παράδειγμα, αν ένα τηλεσκόπιο με διάμετρο πρωτεύοντος 150 mm, έχει εστιακό μήκος 750 mm τότε ο εστιακός λόγος είναι f/5.

Όσο μεγαλύτερος είναι ο εστιακός λόγος τόσο καλύτερη είναι η εικόνα που παίρνουμε από το τηλεσκόπιο, χωρίς όμως αυτό να σημαίνει ότι το τηλεσκόπιο είναι καλύτερα φτιαγμένο οπτικά. Π.χ. Αν δούμε μέσα από δύο τηλεσκόπια ίδιας διαμέτρου και ποιότητας κατασκευής, αλλά με διαφορετικούς εστιακούς λόγους π.χ. f/5 και f/10 τότε η εικόνα που θα πάρουμε από το τηλεσκόπιο με μεγάλο εστιακό λόγο θα είναι καλύτερη. Υπάρχουν βέβαια τηλεσκόπια f/5 με πολύ καλή απόδοση αλλά είναι πιο ακριβά γιατί η κατασκευή τους είναι δυσκολότερη. Στην περίπτωση όμως της αστρονομικής φωτογράφισης μικρότερος εστιακός λόγος συνεπάγεται μικρότερους χρόνους έκθεσης.