3.4 H Υπερβολή

3.4 Η Υπερβολή
Α. Θεωρία	Β. Ασκήσεις
Πακέτο θεωρίας σχολικού βιβλίου	Aσκήσεις ανάπτυξης
Παραμετρικές εξισώσεις καμπύλης	Aσκήσεις πολλαπλής επιλογής
	Aσκήσεις Σωστό - Λάθος
	Aσκήσεις αντιστοίχισης
	Aσκήσεις συμπλήρωσης κενού
	Aσκήσεις διάταξης

	Aσκήσεις Σχολικού βιβλίου
Γ. Εφαρμογές
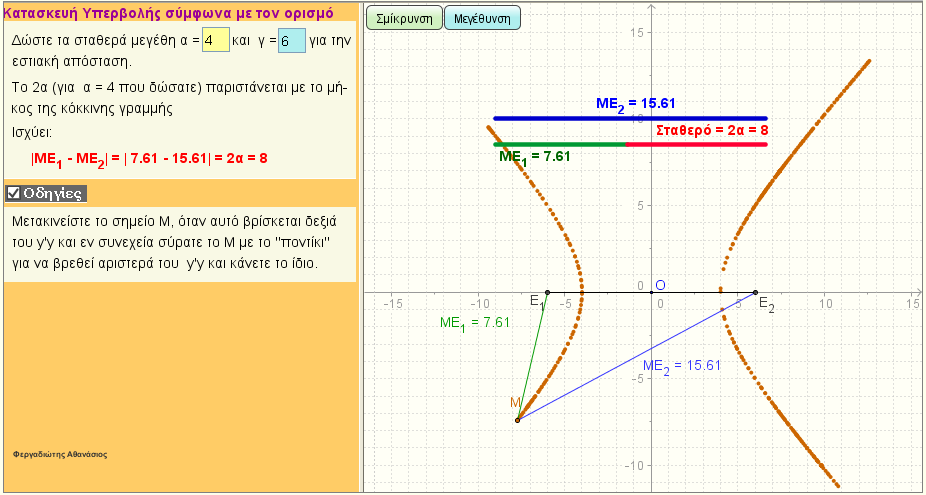
Ορισμός της υπερβολής Η υπερβολή ως γεωμετρικός τόπος σημείων του επιπέδου.

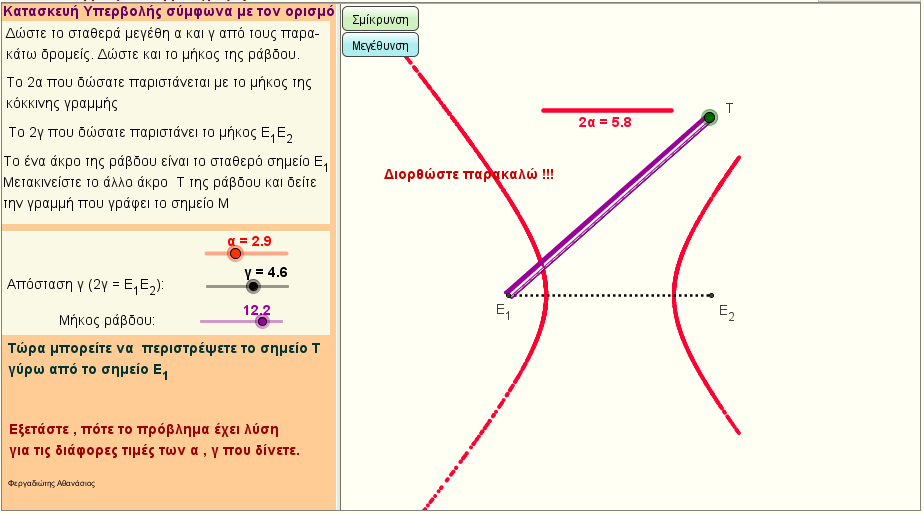
Κατασκευή της Υπερβολής Τρόπος κατασκευής της υπερβολής με ράβδο.

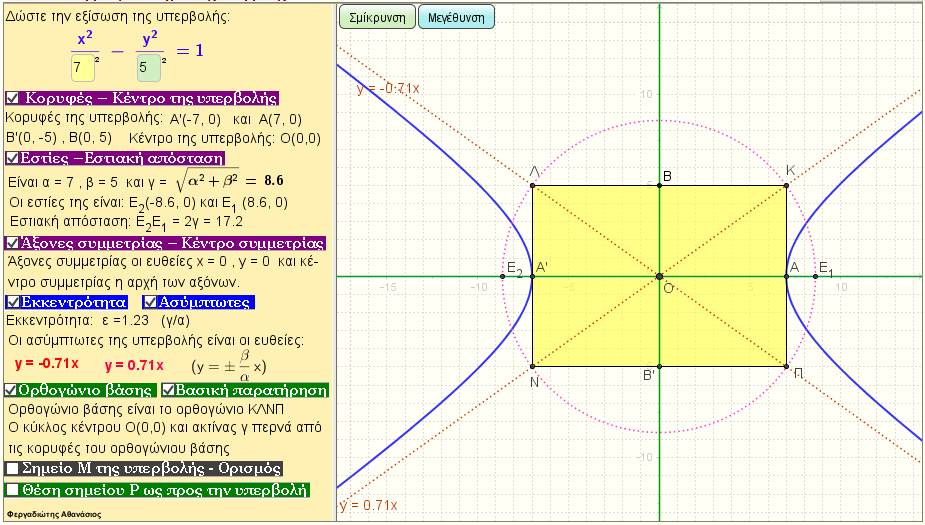
Στοιχεία της υπερβολής 1 Μελέτη της παραβολής x²/α² - y²/β² = 1 Άξονας συμμετρίας , κέντρο συμμετρίας , Κορυφές , Εστίες , Άξονες της έλλειψης ,Μήκη αξόνων , Εκκεντρότητα , Ασύμπτωτες , Ορθογώνιο Βάσης , Εξίσωση εφαπτόμενης σε σημείο της κ.λ.π

Στοιχεία της υπερβολής 2 Μελέτη της παραβολής y²/α² - x²/β² = 1 Άξονας συμμετρίας , κέντρο συμμετρίας , Κορυφές , Εστίες , Άξονες της έλλειψης ,Μήκη αξόνων , Εκκεντρότητα , Ασύμπτωτες , Ορθογώνιο Βάσης , Εξίσωση εφαπτόμενης σε σημείο της κ.λ.π

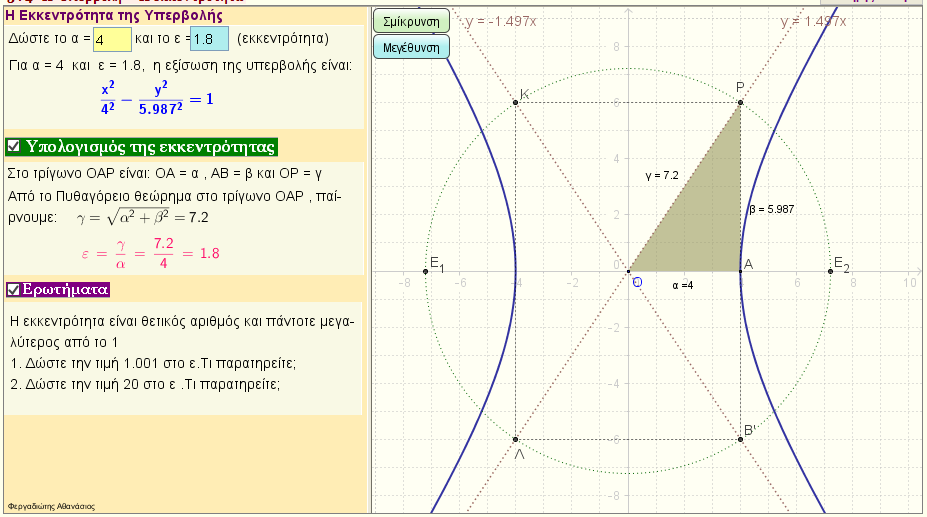
Εκκεντρότητα της υπερβολής Η εκκεντρότητα της υπερβολής ε = γ/α

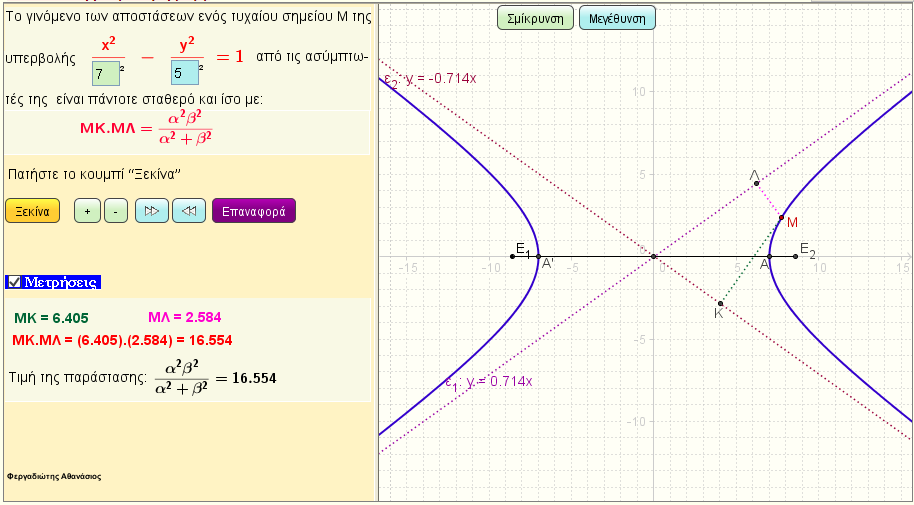
Εφαρμογή Το γινόμενο των αποστάσεων ενός τυχαίου σημείου Μ της υπερβολής x²/α² - y²/β² = 1 , από τις ασύμπτωτές της, είναι πάντοτε σταθερό.

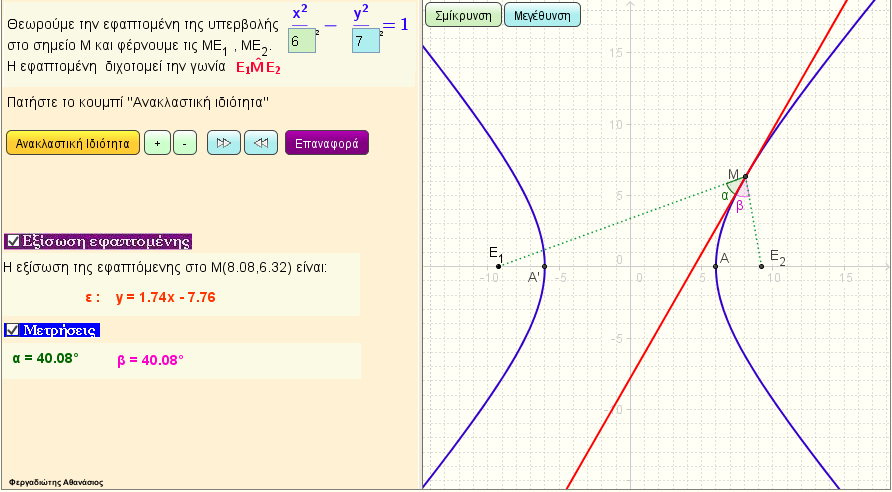
Ανακλαστική ιδιότητα της υπερβολής - Θεωρητικό μέρος Θεωρούμε την εφαπτομένη της υπερβολής στο σημείο Μ , και εκ του Μ φέρουμε τις ευθείες ΜΕ₁ ,ΜΕ₂ ην εφαπτομένη. Η εφαπτομένη διχοτομεί την γωνία Ε₁ΜΕ₂ , όπου Ε₁ , Ε₂ είναι οι εστίες της υπερβολής.

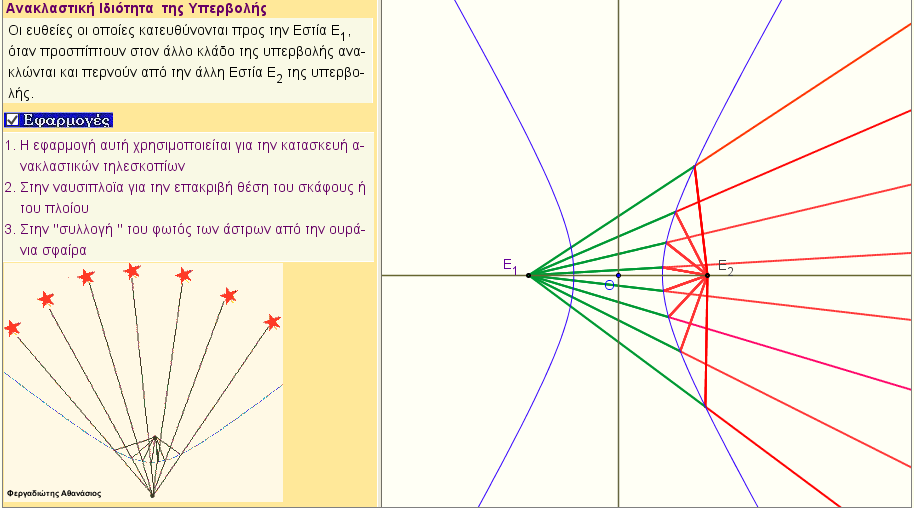
Ανακλαστική ιδιότητα της υπερβολής - Εφαρμογή Οι ευθείες οι οποίες κατευθύνονται στην εστία Ε₁ της υπερβολής ,όταν προσπίπτουν στον άλλο κλάδο της υπερβολής , ανακλώνται , και , περνούν από την άλλη εστία της υπερβολής.

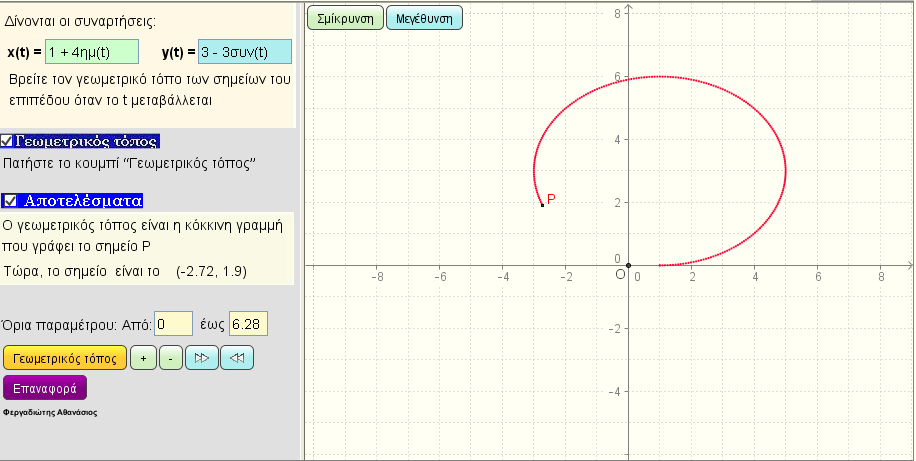
Παραμετρικές εξισώσεις καμπύλης 1 Δώστε τις παραμετρικές εξισώσεις x(t) = ... ,y(t) = .... , ως συνάρτηση του t , και δείτε τον γεωμετρικό τόπο των σημείων Μ(x(t),y(t)) στο επίπεδο.

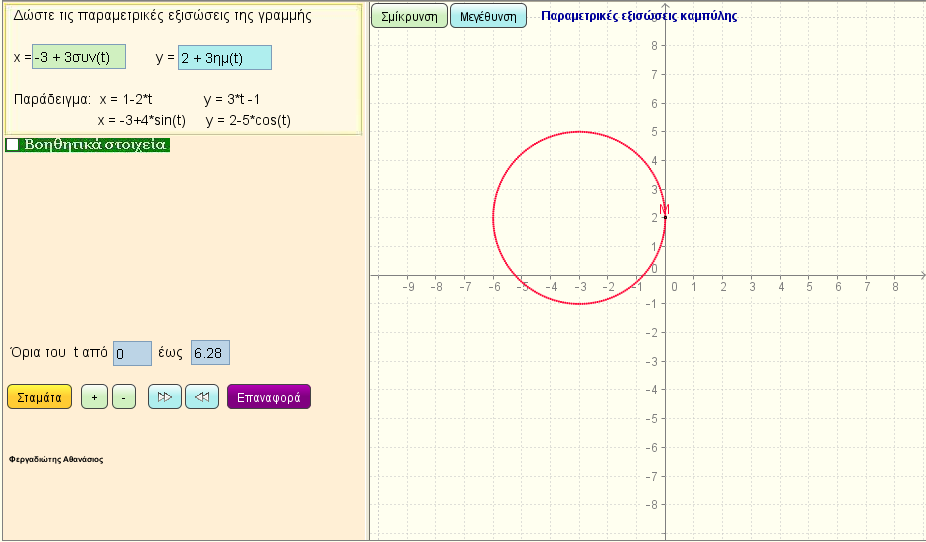
Παραμετρικές εξισώσεις καμπύλης 2 Δώστε τις παραμετρικές εξισώσεις x(t) = ... ,y(t) = .... , ως συνάρτηση του t , και δείτε τον γεωμετρικό τόπο των σημείων Μ(x(t),y(t)) στο επίπεδο.