2.1. Εξίσωση ευθείας

Η εξίσωση της ευθείας

Α΄ Θεωρία			Β΄ Ασκήσεις
Πακέτο θεωρίας σχολικού βιβλίου			Ασκήσεις ανάπτυξης

Γ΄ Τεστ			Ασκήσεις Α΄ ομάδας σχολικού βιβλίου
Η ευθεία			Ασκήσεις B΄ ομάδας σχολικού βιβλίου
Ευθεία που περνά από το Α και έχει γνωστό λ
Συντελεστής διεύθυνσης ευθείας

Δ΄ Εφαρμογές

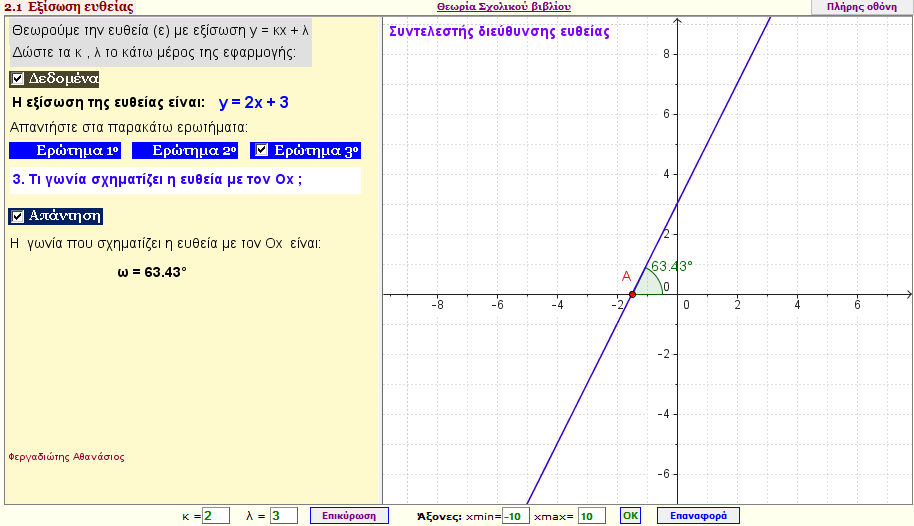
Συντελεστής διεύθυνσης ευθείας Βρείτε τον συντελεστή διεύθυνσης της ευθείας y = κx +λ για τις διάφορες τιμές των κ , λ , καθώς και την γωνία που σχηματίζει αυτή με τον θετικό ημιάξονα Οx.

Tεστ - Συντελεστής διεύθυνσης ευθείας Δίνονται δύο σημεία του επιπέδου. Να βρείτε τον συντελεστή διεύθυνσης της ευθείας που ορίζουν τα σημεία αυτά.

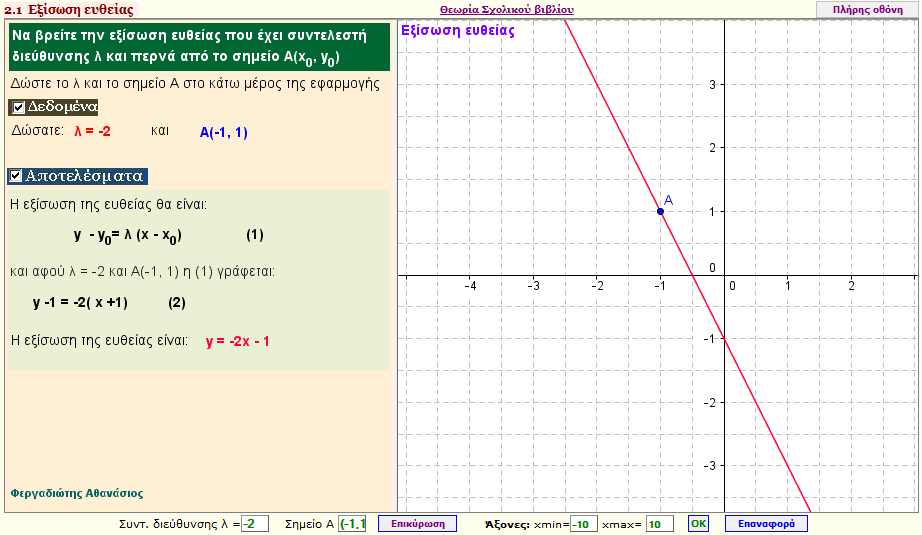
Εξίσωση ευθείας με γνωστό συντελεστή διεύθυνσης λ , που περνά από το σημείο Α(x₀,y₀) Δώστε τον συντελεστή διεύθυνσης της ευθείας και ένα σημείο Α(x₀,y₀) από όπου περνά και βρείτε την εξίσωσή της

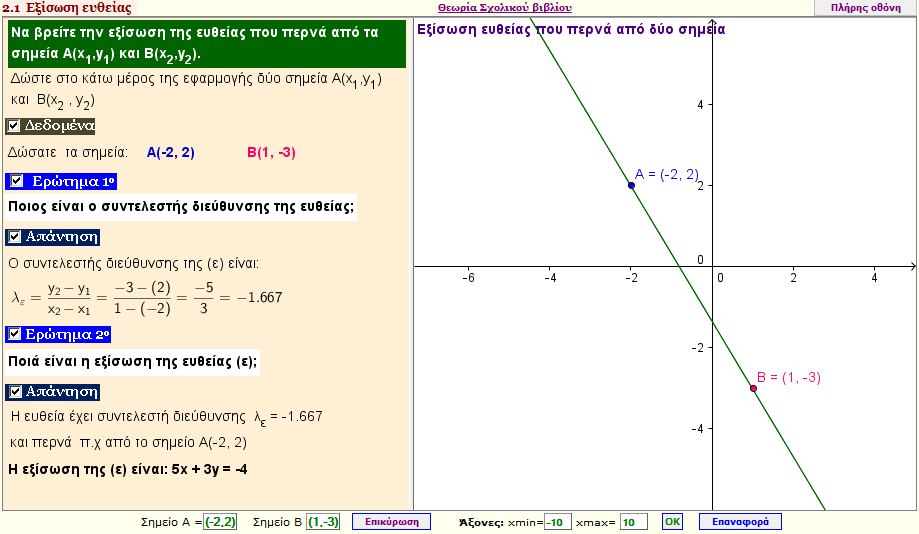
Εξίσωση ευθείας που περνά από τα σημεία Α(x₁,y₁) και Β(x₂,y₂) Δώστε δύο σημεία Α και Β και βρείτε την εξίσωσή της ευθείας ΑΒ

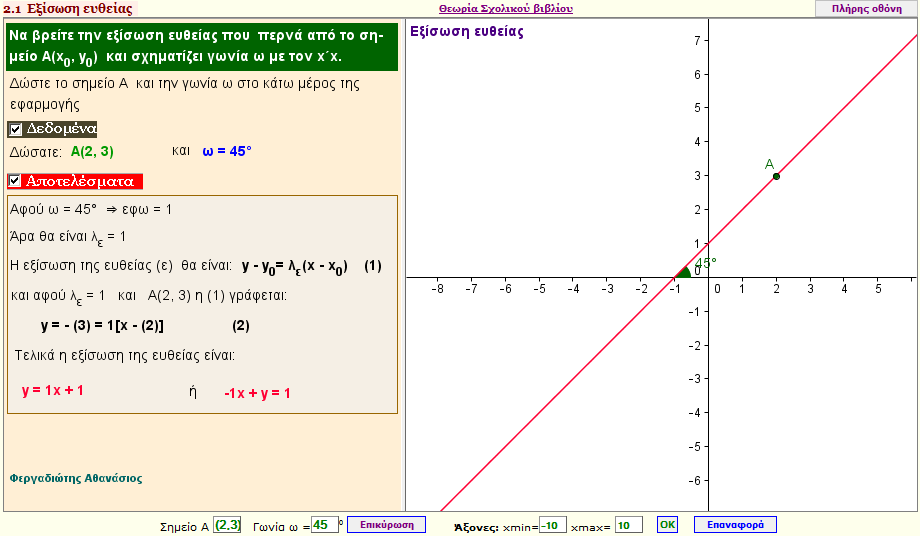
Εξίσωση ευθείας που περνά από το σημείο Α(x₀,y₀) και σχηματίζει γωνία ω με τον x'x Δώστε την γωνία ω = μ⁰ που σχηματίζει η ευθεία με τον x'x και ένα σημείο Α(x₀,y₀) από όπου περνά και βρείτε την εξίσωσή της

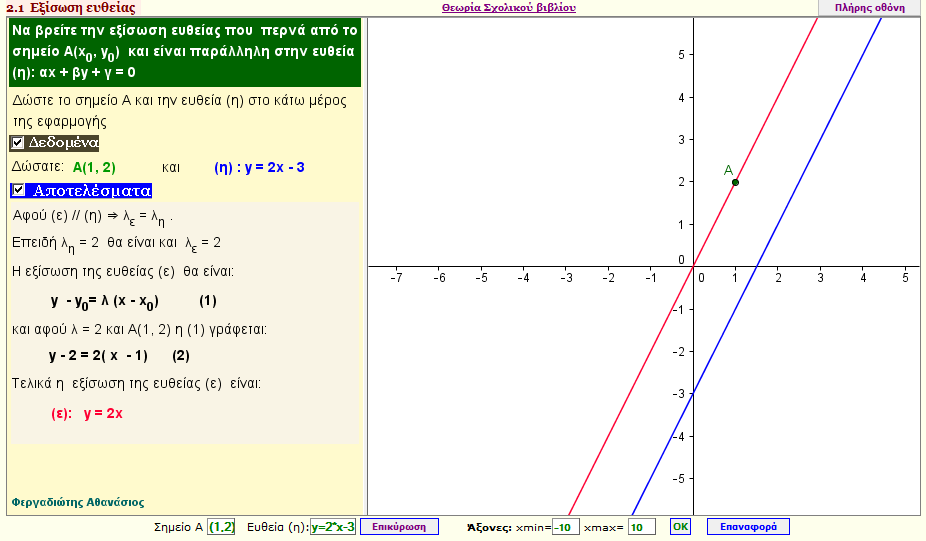
Εξίσωση ευθείας που περνά από το Α(x₀,y₀) και είναι παράλληλη σε δοσμένη ευθεία (η): αx + βy + γ = 0 Βρείτε την εξίσωση της ευθείας που περνά από ένα δοσμένο σημείο Α(x₀,y₀) και είναι παράλληλη σε δοσμένη ευθεία (η) : αx+ βy + γ = 0

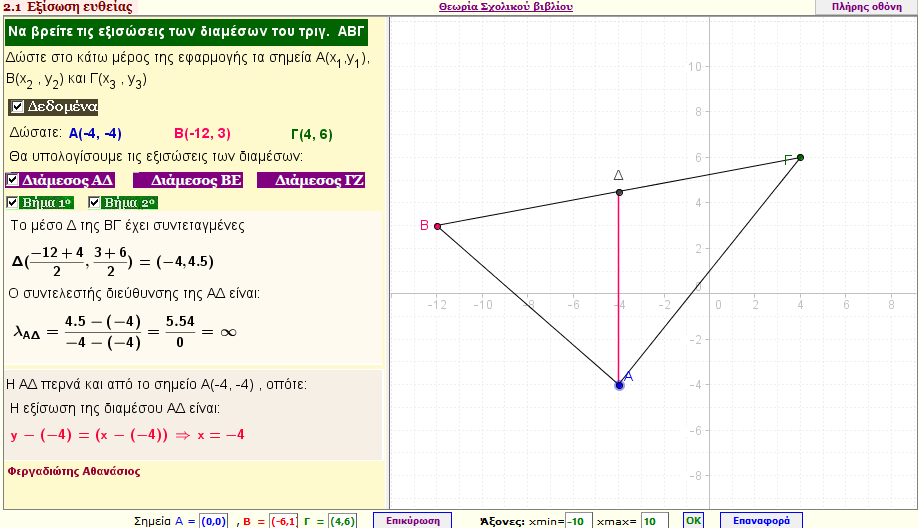
Εξισώσεις των διαμέσων ενός τριγώνου Βρείτε τις εξισώσεις των διαμέσων ενός τριγώνου ΑΒΓ , αν γνωρίζετε τις κορυφές Α(x₁,y₁) , Β(x2,y₂) , και Γ(x₃,y₃) του τριγώνου ΑΒΓ

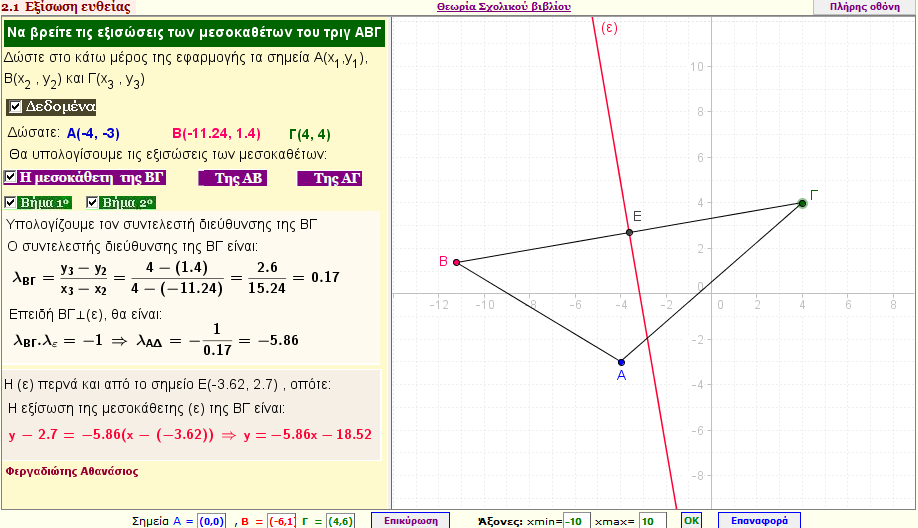
Εξισώσεις των μεσοκαθέτων ενός τριγώνου Βρείτε τις εξισώσεις των μεσοκαθέτων ενός τριγώνου ΑΒΓ , αν γνωρίζετε τις κορυφές Α(x₁,y₁) , Β(x2,y₂) , και Γ(x₃,y₃) του τριγώνου ΑΒΓ

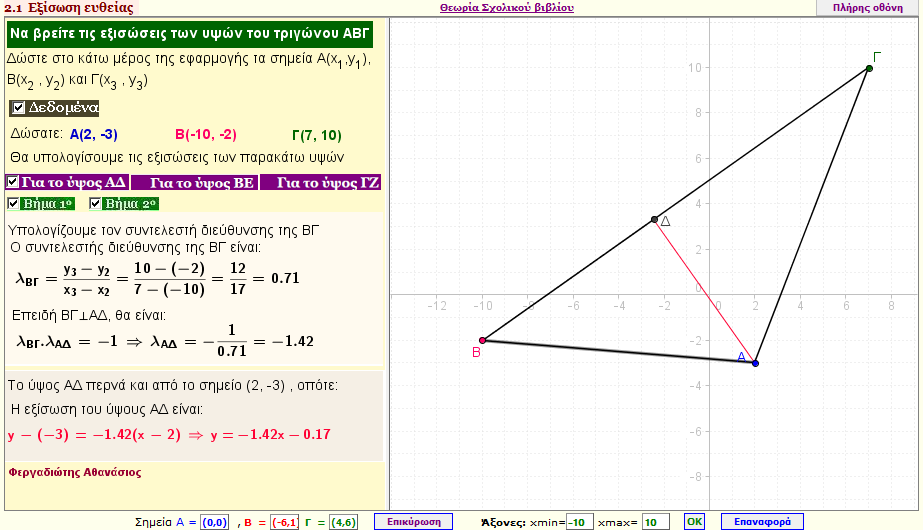
Εξισώσεις των υψών ενός τριγώνου Βρείτε τις εξισώσεις των υψών ενός τριγώνου ΑΒΓ , αν γνωρίζετε τις κορυφές Α(x₁,y₁) , Β(x2,y₂) , και Γ(x₃,y₃) του τριγώνου ΑΒΓ

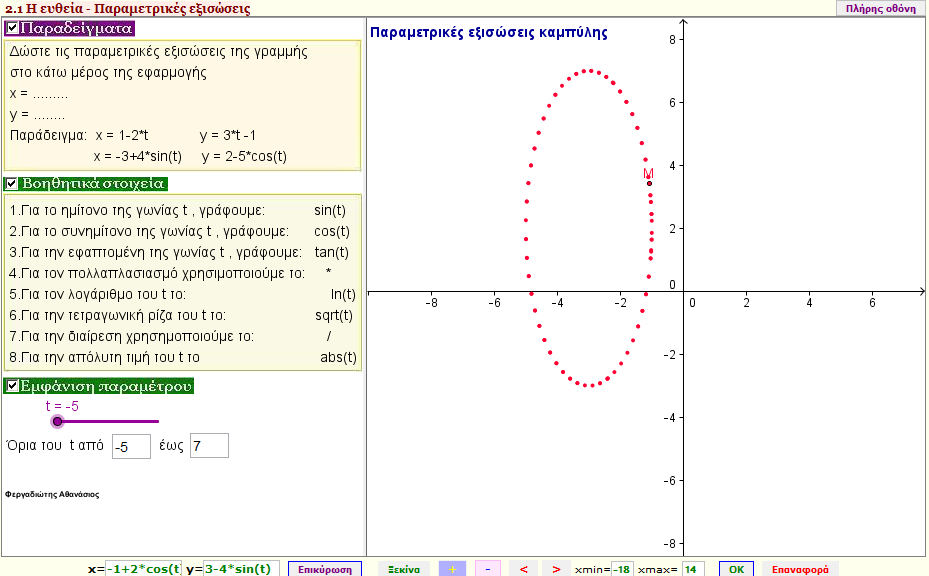
Παραμετρικές εξισώσεις ευθείας Όταν σας δοθεί το σημείο Μ(αt +β , γt + δ) , ποιος είναι ο γεωμετρικός τόπος των σημείων Μ καθώς το t μεταβάλλεται , και τα α , β , γ , δ είναι σταθερά;

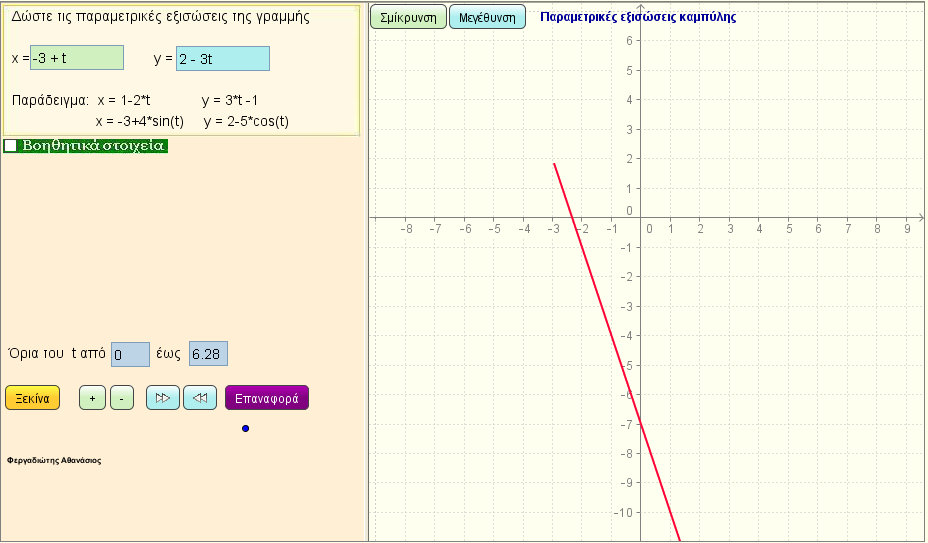
Παραμετρικές εξισώσεις ευθείας1 Οι παραμετρικές εξισώσεις ευθείας που περνά από το σημείο Μ(α,β) και είναι παράλληλη στο διάνυσμα (κ,λ) είναι: x = α+κt , y = β +λt , με t τυχαίο πραγματικό αριθμό.

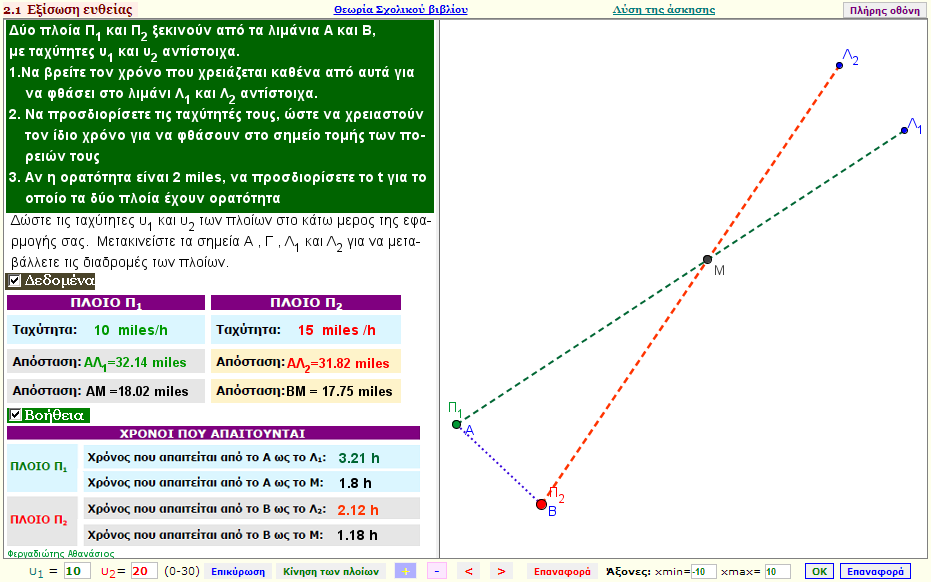
Πρόβλημα με πλοία Ένα πρόβλημα με δύο πλοία που ξεκινούν από διαφορετικά ή το ίδιο λιμάνι , που έχουν γνωστές ταχύτητες , και πρόκειται να φθάσουν σε διαφορεικά λιμάνια ή στο ίδιο λιμάνι.Για να φθάσουν συγχρόνως στον προορισμό τους , θα πρέπει να μεταβάλλουμε κατάλληλα τις ταχύτητές τους.Αν σας δοθεί και μιά απόσταση α , πότε τα πλοία θα έχουν οπτική επαφή;