| 2.1 - Tετραγωνική ρίζα θετικού αριθμού |
|
|
|
| Θεωρία |
|
|
Ασκήσεις |
| Πακέτο θεωρίας σχολικού βιβλίου |
|
|
Λύσεις ασκήσεων σχολικού βιβλίου και ερωτήσεων κατανόησης |
| |
|
|
|
| Εφαρμογές |
|
|
|
| |
|
|
|
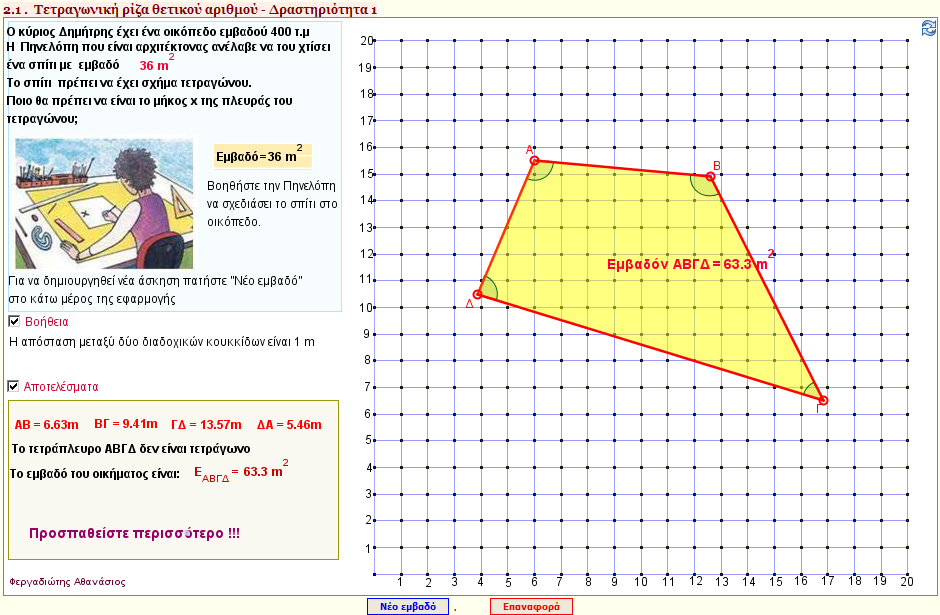
Δραστηριότητα 1
O κύριος Δημήτρης έχει ένα οικόπεδο 400 τετρ. μέτρων
Μπορείτε να βοηθήσετε την Πηνελόπη που είναι αρχιτέκτονας να σχεδιάσει ένα σπίτι α τετρ. μέτρων με τετραγωνική βάση στο οικόπεδο αυτό; |
|
|
 |
| |
|
|
|
Πίνακες τετραγωνικών ριζών
Δώστε μια τιμή στο α (από 1 έως 99934) και η εφαρμογή θα υπολογίσει ποιοι είναι οι αριθμοί που οι ρίζες τους παίρνουν τιμές από α έως α + 65. |
|
|
 |
| |
|
|
|
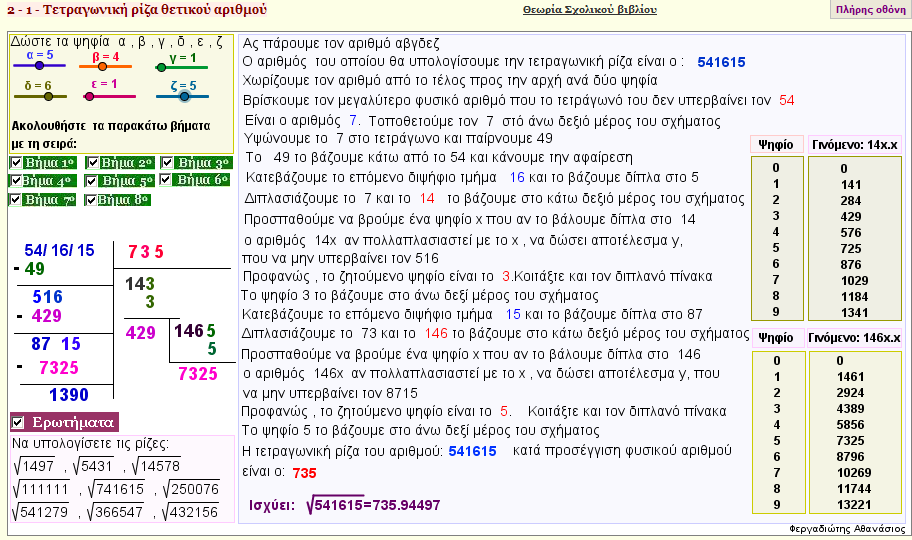
Αλγόριθμος εύρεσης τετραγωνικής ρίζας θετικού αριθμού
Με ποιον τρόπο βρίσκουμε την τετραγωνική ρίζα ενός θετικού αριθμού α;
Ο παραπάνω αλγόριθμος βρίσκει την τετραγωνική ρίζα ενός εξαψήφιου αριθμού.
Ακολουθείστε ένα προς ένα τα βήματα της παραπάνω εφαρμογής. |
|
|
 |
| |
|
|
|
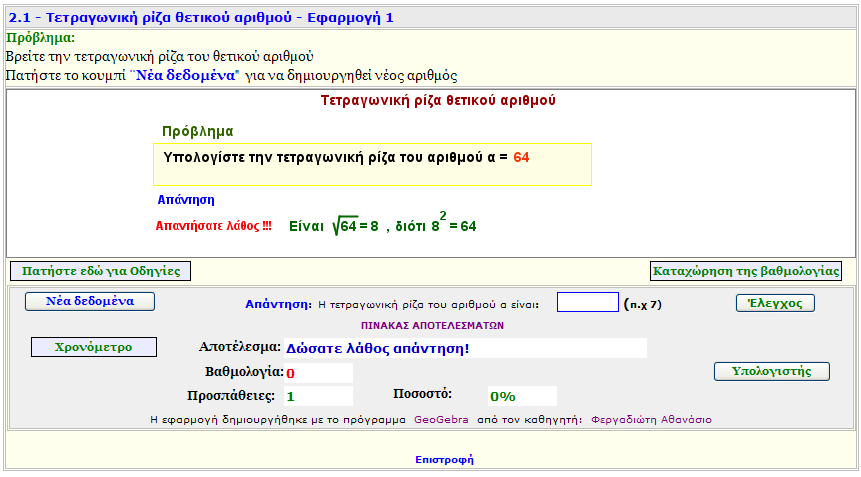
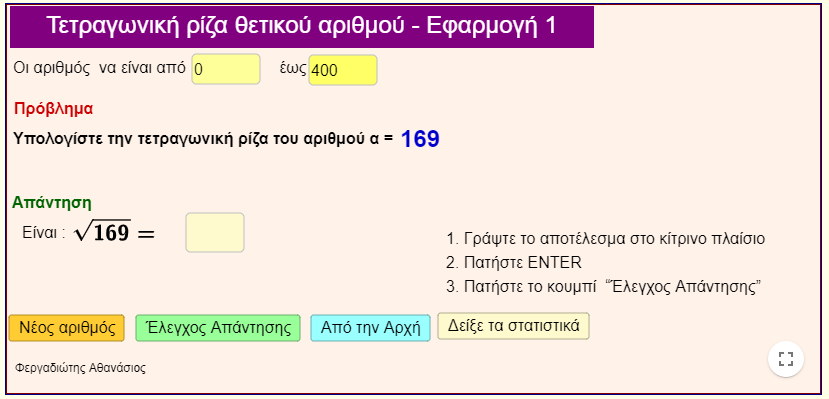
Εφαρμογή 1
Βρείτε τη τετραγωνική ρίζα ενός θετικού αριθμού α.
Εξάσκηση. |
|
|
 |
| |
|
|
|
Εφαρμογή 1 - Πρακτική εξάσκηση
Βρείτε τη τετραγωνική ρίζα ενός θετικού αριθμού α.
Απαντήστε σωστά και μαζέψτε , όσους περισσσότερους βαθμούς μπορείτε.
Η βαθμολογία σας κατοχυρώνεται μόνο αν είναι μεγαλύτερη από 139 βαθμούς. |
|
|
 |
| |
|
|
|
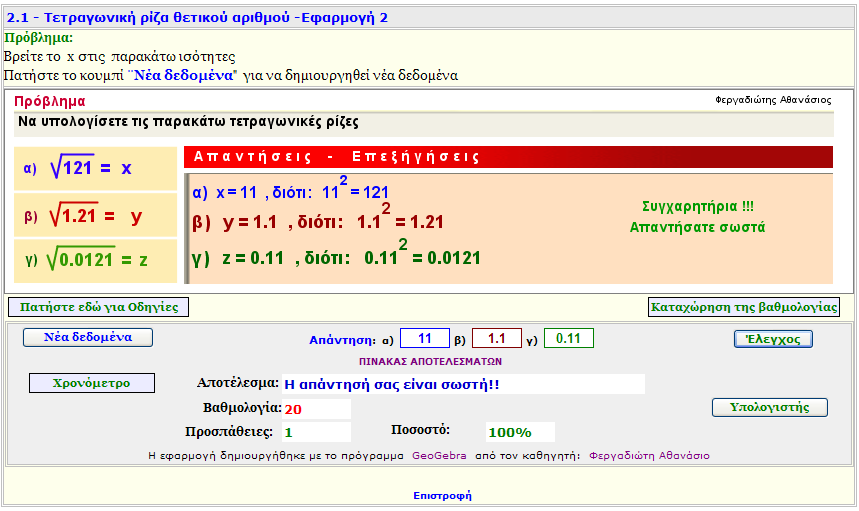
Εφαρμογή 2
Βρείτε τη τετραγωνική ρίζα ενός θετικού αριθμού και δύο θετικώνδεκαδικών αριθμών.
Εξάσκηση |
|
|
 |
| |
|
|
|
Εφαρμογή 2 -Πρακτική εξάσκηση
Βρείτε τη τετραγωνική ρίζα ενός θετικού αριθμού και δύο θετικών δεκαδικών αριθμών.
Στην πρακτική αυτή εξάσκηση πρέπει να δώσετε τρείς απαντήσεις.
Για να πάρετε τους βαθμούς , θα πρέπει να απαντήσετε σε όλες σωστά.
Η βαθμολογία σας κατοχυρώνεται μόνο αν είναι μεγαλύτερη από 139 βαθμούς |
|
|
 |
| |
|
|
|
Εφαρμογή 3
Βρείτε την υποτείνουσα ενός ορθογωνίου τριγώνου , όταν γνωρίζετε τις κάθετες πλευρές του.
Εξάσκηση.
|
|
|
 |
| |
|
|
|
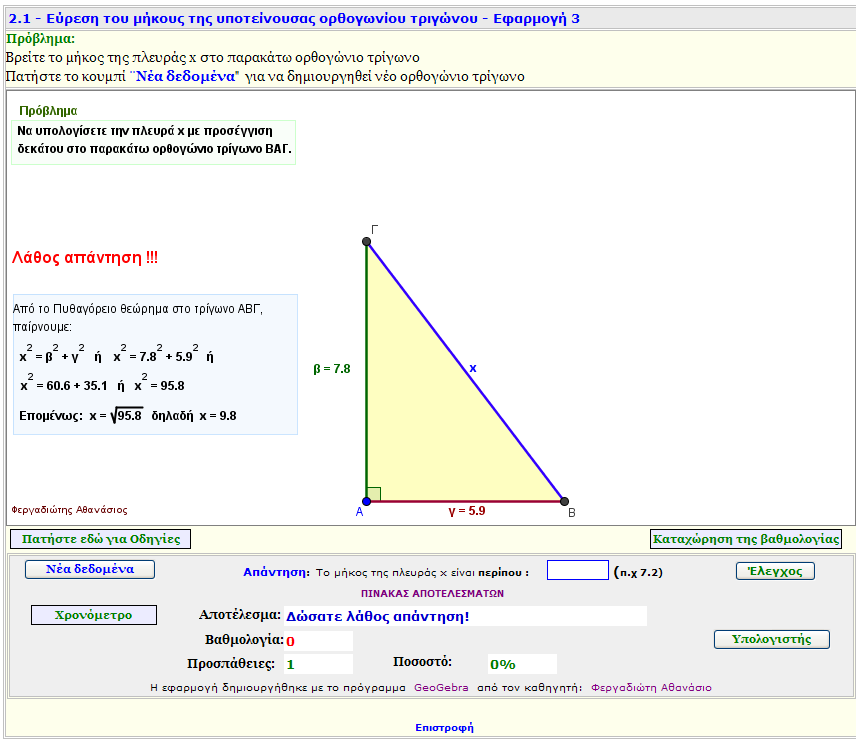
Εφαρμογή 3
Βρείτε την υποτείνουσα ενός ορθογωνίου τριγώνου , όταν γνωρίζετε τις κάθετες πλευρές του.
Πρακτική εξάσκηση.
Απαντήστε σωστά και μαζέψτε , όσους περισσσότερους βαθμούς μπορείτε.
Η βαθμολογία σας κατοχυρώνεται μόνο αν είναι μεγαλύτερη από 139 βαθμούς. |
|
|
 |
| |
|
|
|
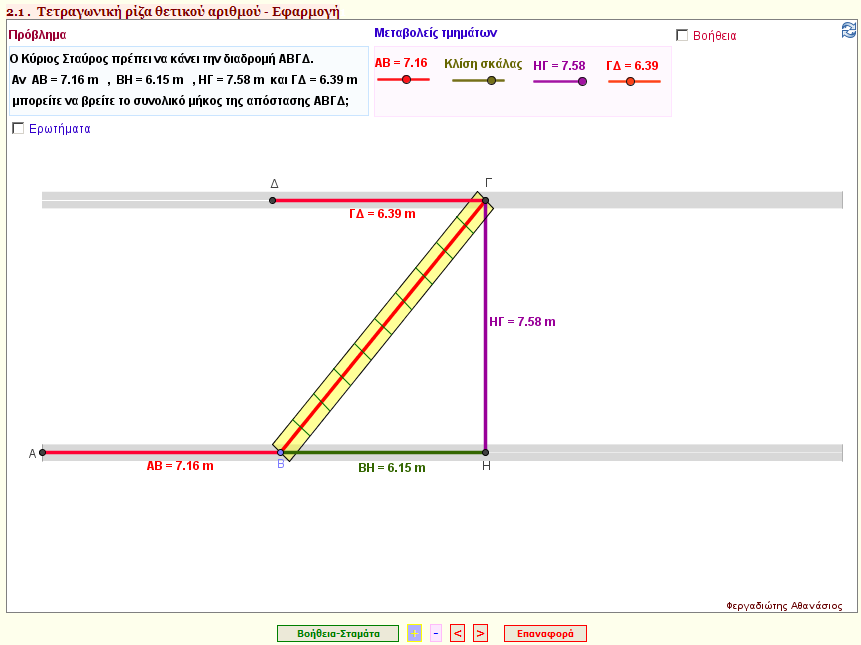
Εφαρμογή 4
H κυρία Ελένη βρίσκεται στον πρώτο όροφο ενός κτιρίου και πρόκειται να πάει στον δεύτερο όροφο του κτιρίου, για να αγοράσει ένα παντελόνι, αφού διασχίσει την σκάλα που συνδέει τον πρώτο με τον δεύτερο όροφο.
Ποιο θα είναι το συνολικό μήκος που θα διασχίσει; |
|
|
 |
| |
|
|
|
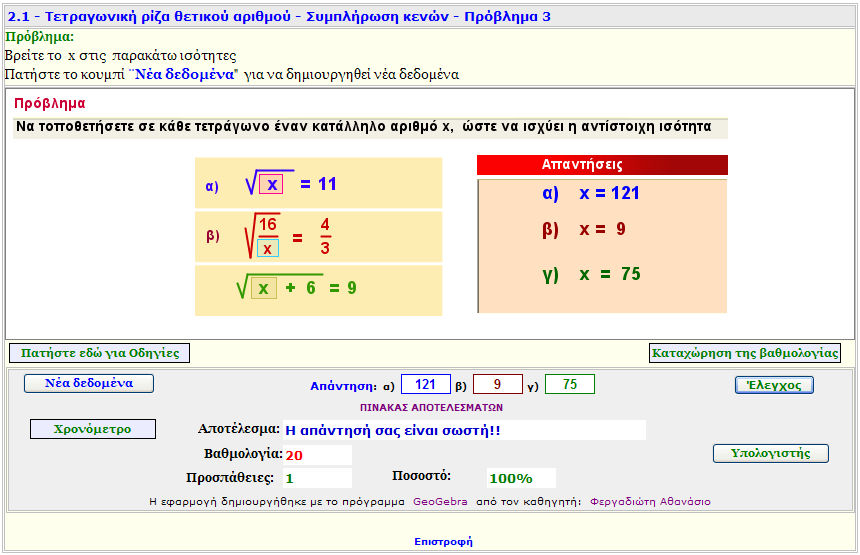
Πρόβλημα 3
Βρείτε το x στις τετραγωνικές ρίζες στις οποίες εμφανίζεται. Εξάσκηση |
|
|
 |
| |
|
|
|
Πρόβλημα 3
Βρείτε το x στις τετραγωνικές ρίζες στις οποίες εμφανίζεται και κερδίστε 20 βαθμούς για κάθε σωστή απάντηση.
Στην πρακτική αυτή εξάσκηση πρέπει να δώσετε τρείς απαντήσεις.
Για να πάρετε τους βαθμούς , θα πρέπει να απαντήσετε σε όλες σωστά.
Η βαθμολογία σας κατοχυρώνεται μόνο αν είναι μεγαλύτερη από 139 βαθμούς |
|
|
 |
| |
|
|
|
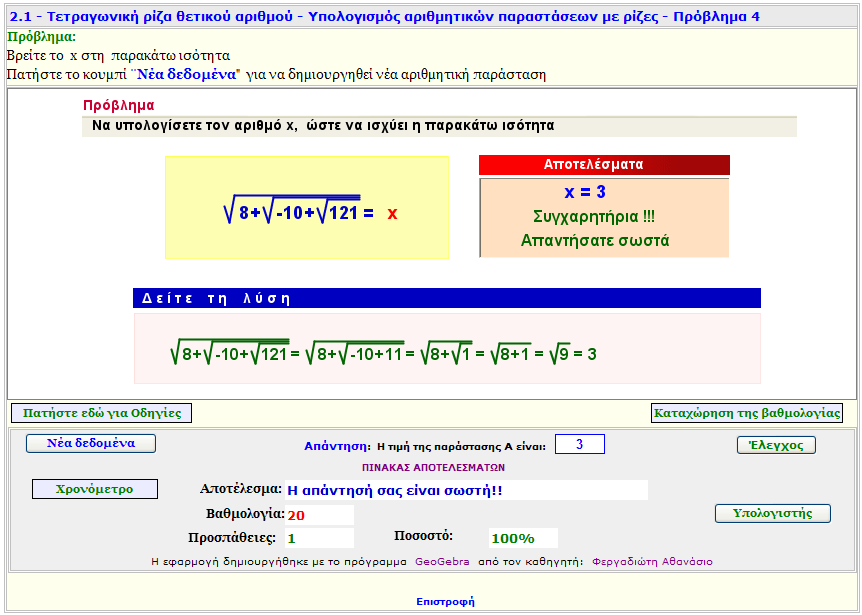
Πρόβλημα 4
Βρείτε τη τιμή x της τετραγωνικής ρίζας, της οποίας η υπόριζη ποσότητα περιέχει άλλες ρίζες.
Εξάσκηση.
|
|
|
 |
| |
|
|
|
Πρόβλημα 4
Βρείτε τη τιμή x της τετραγωνικής ρίζας, της οποίας η υπόριζη ποσότητα περιέχει άλλες ρίζες.Σε κάθε ερώτηση που εμφανίζεται κερδίζετε 20 βαθμούς για κάθε σωστή απάντηση.
Πρακτική εξάσκηση.
Η βαθμολογία σας κατοχυρώνεται μόνο αν είναι μεγαλύτερη από 139 βαθμούς. |
|
|
 |
| |
|
|
|
Πρόβλημα 11
Ποιος από του αριθμούς α , α2 , είναι ο μεγαλύτερος;
Να κάνετε μια πλήρη διερεύνηση για όλες τις τιμές του α |
|
|
 |
| |
|
|
|
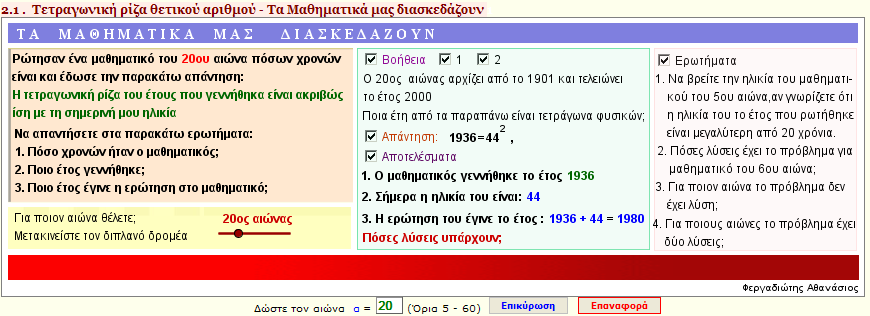
Tα μαθηματικά μας διασκεδάζουν
Ρωτήθηκε ένας μαθηματικός του α αιώνα πόσο ετών είναι και έδωσε την εξής απάντηση:
Η τετραγωνική ρίζα του έτους που γεννήθηκα είναι η σημερινή μου ηλικία.
Πόσων ετών είναι ο μαθηματικός;
Πότε γεννήθηκε;
Πότε του έγινε αυτή η ερώτηση; |
|
|
 |