Οι ασκήσεις του μήνα

  Αρχείο ασκήσεων Α' Λυκείου

  Αρχείο ασκήσεων Β' Λυκείου

  Αρχείο ασκήσεων Γ' Λυκείου

  Αρχείο γενικών ασκήσεων

Βαθμοί

Τεστ - διαγωνίσματα Φυσικής

Πειράματα Φυσικής

Έφηβοι

Περιοδικά-Βιβλία-Εγκυκλοπαίδειες

Παιχνίδια σκέψης

Τα 10 μεγαλύτερα τεχνολογικά σκάνδαλα της δεκαετίας

10 παγκόσμια γεωλογικά θαύματα

Το 2012 στο Διάστημα

Οι καλύτερες ανακαλύψεις που έγιναν το 2012

Τα σημαντικότερα επιτεύγματα του 2012 σύμφωνα με το Science

Οι καλύτερες φωτογραφίες του 2012 σύμφωνα με το περιοδικό National Geographic

-----------------------------------------------

(New) Μαθήματα και εξετάσεις Νέου Λυκείου

1905-2005

Οι ασκήσεις 

Α΄ Λυκείου  ------------------------------------------

«Όχι στον άδικο αποκλεισμό!» Δεκ 13*

Σ΄ έναν αγώνα αυτοκινήτων η κριτική επιτροπή έχει βάλει σαν βασικό όρο για την συμμετοχή, να μπορεί το αυτοκίνητο να διατρέξει, από την ακινησία, τα 200 m το πολύ σε 10 δευτερόλεπτα. Ο Τοτός, στη λαχτάρα του να μπορέσει να συμμετάσχει, «κατά λάθος» όπως ισχυρίζεται, τη χρονική στιγμή t = 0 δεν έχει πλήρως ακινητοποιήσει το αυτοκίνητο του, αλλά του έχει δώσει ταχύτητα 9 m/s. Το αποτέλεσμα είναι να κάνει τα 200 m σε 8 s, αλλά να αποκλειστεί από την επιτροπή. Παρά ταύτα ο Τοτός κάνει ένσταση, δικαιώνεται και τελικά παίρνει μέρος στον αγώνα. Ποια ήταν νομίζετε τα επιχειρήματα του;

(Θεωρείστε ότι η αντίσταση του αέρα και γενικότερα οι τριβές κατά τη κίνηση του αυτοκινήτου είναι ίδιες σε κάθε περίπτωση)

Αρχείο ασκήσεων Α΄ Λυκείου  >>>>

Β΄ Λυκείου  ------------------------------------------

«Μέχρι πόσο μπορεί να σηκωθεί το 1ο χωρίς να κοπεί το 2ο;» Δεκ 13**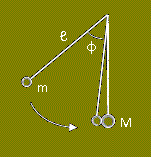 

Δύο νήματα, μήκους ℓ = 10 m το καθένα, έχουν πιασμένα τα πάνω άκρα τους στο ίδιο σταθερό σημείο, ενώ στα ελεύθερα άκρα τους φέρουν μικρές σφαίρες μάζας m = 1 Kg και M = 2 Kg. Αρχικά και τα δύο νήματα ηρεμούν στην κατακόρυφο, ενώ οι σφαίρες ακουμπούν η μία δίπλα στην άλλη. Κάποια στιγμή απομακρύνουμε την m από την κατακόρυφο κατά γωνία φ και την αφήνουμε ελεύθερη. Για λόγους ευκολίας θεωρούμε ότι κατά τη κρούση των δύο σφαιρών η m ακινητοποιείται μετά την κρούση. Αν ξέρουμε ότι το όριο θραύσης των νημάτων είναι 25 Ν, πόση είναι η μέγιστη γωνία που μπορούμε να απομακρύνουμε την m από την κατακόρυφο, χωρίς να σπάσει το νήμα που κρατά την M;

Δίνεται g = 10 m/s². Θεωρείστε α) ότι οι τριβές θεωρούνται αμελητέες και β) ότι οι σφαίρες είναι υλικά σημεία.

Αρχείο ασκήσεων Β΄ Λυκείου  >>>>

Γ΄ Λυκείου  ------------------------------------------

«Άλλα δύο ίδια μέχρι τη μεσοκάθετο» Δεκ 13**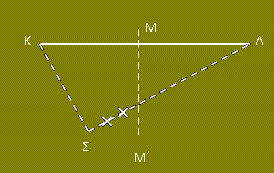 

Στην οριζόντια επιφάνεια ενός μέσου διάδοσης έχουμε δύο σύμφωνες πηγές στα σημεία Κ και Λ. Οι πηγές ταλαντώνονται με ίδιο πλάτος Α και συχνότητα f = 2 Hz και τα κύματα διαδίδονται με ταχύτητα υ_δ = 6 m/s. Σημείο Σ της επιφάνειας, όταν αρχίζει η συμβολή, ταλαντώνεται με πλάτος Α_Σ = Α. Αν πάνω στο ευθύγραμμο τμήμα ΣΛ, μέχρι τη μεσοκάθετο, υπάρχουν άλλα δύο σημεία με το ίδιο πλάτος ταλάντωσης (σχήμα), πόση είναι διαφορά δρόμου ΣΛ – ΣΚ του σημείου Σ από τις πηγές;

Αρχείο ασκήσεων Γ' Λυκείου  >>>>

Στείλτε την λύση σας στο  fil_platakis@yahoo.gr

Διευκρινίσεις:

Οι ασκήσεις που δημοσιεύονται κάθε μήνα στην ιστοσελίδα απευθύνονται κυρίως σε μαθητές Λυκείου και είναι εμπνεύσεις του διεστραμμένου εγκεφάλου του υπογράφοντα. Συνεπώς δεν έχει νόημα να ρωτάτε από ποιο βιβλίο αντιγράφονται, γιατί δεν υπάρχει τέτοιο βιβλίο. Για λόγους δεοντολογίας, στις σπάνιες περιπτώσεις που η βασική ιδέα της άσκησης βρίσκεται σε κάποιο βιβλίο ή έχει προταθεί από κάποιον συνάδελφο, το όνομα του αναφέρεται μετά την εκφώνηση της.

Επίσης δεν έχει κανένα νόημα να συσχετίζετε τις ασκήσεις με τεστ, διαγωνίσματα ή εξετάσεις (πολύ περισσότερο Πανελλήνιες). Physιcs is fun. Λύστε για τον εαυτό σας και μόνο. Αν τώρα θέλετε να δημοσιευτεί το όνομα σας, στείλτε με e-mail τις λύσεις σας, για να "περάσετε στην αθανασία" και παράλληλα να χαροποιήσετε και τον συντάκτη της ιστοσελίδας.

Καλή τύχη στις προσπάθειες σας...