Μελέτη της συνάρτησης f(x)=εφx
Γιώργος Μαντζώλας - Δημιουργήθηκε με GeoGebra στις 25-11-2007
Δεδομένα:
1) εφω=τεταγμένη του σημείου Σ. 2) Η συνάρτηση εφαπτομένη
f(x)=εφx, (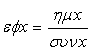 )
)
δεν ορίζεται όταν
το συν μηδενίζεται. 3) Για όλα τα x που ΔΕΝ
μηδενίζουν το συν ισχύει: εφ(x+π)=εφ(x-π)=εφx,
επομένως η συνάρτηση εφαπτομένη είναι περιοδική με περίοδο π και αρκεί να
μελετηθεί σε ένα διάστημα πλάτους π, π.χ. ![]()
Οδηγίες χρήσης: Μπορείτε να περιστρέψετε το σημείο Κ για να μεταβάλετε τη γωνία ω.
Ερωτήσεις:
1) Ποιο είναι το είδος της μονοτονίας της συνάρτησης
f(x)=εφx
στο διάστημα ![]() ;
;
2) Όταν το x πλησιάζει στο π/2 με τιμές μικρότερες του π/2, που κινούνται οι τιμές της εφx; 3) Όταν το x πλησιάζει στο π/2 με τιμές μεγαλύτερες του π/2, που κινούνται οι τιμές της εφx;
4) Ποιες
είναι οι λύσεις της εξίσωσης
εφx=0; 5)
Η γραφική παράσταση της συνάρτησης
f(x)=εφx
συναντά την ευθεία ![]() ;
;