Ανδρέας Ιωάννου Κασσέτας

Το σχέδιο της αφίσας World Year of Physics 2005

παριστάνει τον κώνο φωτός του Minkowski .

Ας τον «φωτίσουμε»

Οι τέσσερις διαστάσεις και η ταχύτητα του φωτός.

Το 1906 ο Henry Poincaré παρουσίασε μία μαθηματική τυπολογία στον τετραδιάστατο χώρο, με τον ΧΡΟΝΟ ΩΣ ΤΕΤΑΡΤΗ ΔΙΑΣΤΑΣΗ. Ωστόσο δεν αναφέρθηκε σε καμία γεωμετρική πτυχή αυτής της διαδικασίας αλλά και δεν συνειδητοποίησε την αξία της ιδέας. Αυτό το έκανε ένας άλλος μαθηματικός. O Ρωσογερμανός Hermann Minkowski.

ο Hermann Minkowski.

Το 1907 ο Hermann Minkowski, καθηγητής τότε των Μαθηματικών στο Πανεπιστήμιο του Götingen, διέκρινε ότι πως η μαθηματική μέθοδος του Poincaré έθετε τις βάσεις για μία γεωμετρική διατύπωση της Ειδικής θεωρίας της Σχετικότητας στον τετραδιάστατο χώρο που θα συμπεριλάμβανε και οπτικές παραστάσεις. Συνειδητοποίησε ότι το στοιχείο που συνδέει τις τέσσερις διαστάσεις είναι η ταχύτητα του φωτός. Στο “ Raum und Zeit” που κυκλοφόρησε το 1908 είπε καθαρά ότι «Από δω και πέρα ο χρόνος καθεαυτόν και ο χώρος καθεαυτόν είναι καταδικασμένοι να ξεθωριάσουν, να γίνουν σκιές και μόνο ένα είδος ένωσης των δύο θα διατηρήσει μια αυθύπαρκτη υπόσταση».

Στην εργασία του αυτή παρουσίασε μία κομψή μαθηματική έκφραση για τον μετασχηματισμό των συντεταγμένων του χώρου και του χρόνου, εισάγοντας την έννοια ΤΕΤΡΑΔΙΑΣΤΑΤΟΣ ΧΩΡΟΣ με τρεις συντεταγμένες χώρου και μία χρόνου. Το ιδιαίτερο χαρακτηριστικό του χώρου αυτού είναι ότι η απόσταση δύο σημείων δεν δίνεται από το Πυθαγόρειο θεώρημα, που για τον κοινό τρισδιάστατο χώρο έχει τη μορφή s² = x² + y² + z². Στον τετραδιάστατο χώρο του Minkowski η απόσταση δύο σημείων - γεγονότων δίνεται από τη σχέση s² = x² + y² + z²- c²t² .

Για να γίνει αυτό οι τρεις άξονες είναι βαθμολογημένοι με τις χωρικές συντεταγμένες x, y , z, αλλά ο «τέταρτος άξονας» είναι βαθμολογημένος με τις τιμές ict όπου i η φανταστική μονάδα για την οποία i² = -1.

Ένα βότσαλο στη λίμνη.

Σε κάποια χρονική στιγμή – αρχή των χρόνων – ρίχνουμε ένα βότσαλο στη λίμνη και παίρνουμε φωτογραφίες ανά ίσους χρόνους. Το πρώτο στιγμιότυπο είναι το «γεγονός» της συνάντηση του βότσαλου με την ακίνητη επιφάνεια του νερού και αντιστοιχεί σε ένα σημείο ενώ τα υπόλοιπα στιγμιότυπα αντιστοιχούν σε εικόνες κύκλων καθένας από τους οποίους έχει ακτίνα ίση με το γινόμενο «ταχύτητα διάδοσης του κύματος επί χρόνο» . Αν τοποθετήσουμε τις φωτογραφίες σε οριζόντια επίπεδα τα οποία να ισαπέχουν, τα άκρα των οριζόντιων κύκλων θα ανήκουν στην επιφάνεια ενός κώνου με την κορυφή προς τα κάτω. Κάθε σημείο της κωνικής αυτής επιφάνειας αναπαριστά ένα ΓΕΓΟΝΟΣ την άφιξης του κύματος σε κάποιο σημείο του χώρου και του χρόνου. Τα σημεία του εσωτερικού της κωνικής επιφάνειας αντιστοιχούν σε ενδεχόμενες αφίξεις υποθετικών κυμάτων που διαδίδονται με μικρότερη ταχύτητα.

Ο κώνος φωτός Κώνος του Minkowski.

Κατά ανάλογο τρόπο μπορούμε να αναπαραστήσουμε το φαινόμενο «εκπομπή ενός ηλεκτρομαγνητικού σήματος» σε ένα υποθετικό χώρο δύο χωρικών διαστάσεων χρησιμοποιώντας άξονες 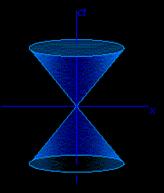x και y και τρίτο άξονα με τιμές τα γινόμενα «ταχύτητα του σήματος επί τον χρόνο» ct . Με αρχή των αξόνων το γεγονός «εκπομπή του σήματος» ΤΩΡΑ, το γεγονός «άφιξη του σήματος σε κάποιο χωροχρονικό σημείο του μέλλοντος» θα παριστάνεται με ένα γεωμετρικό σημείο της κωνικής επιφάνειας με την κορυφή προς τα κάτω και - εφόσον κατά για τη διάδοση του σήματος στις δύο διαστάσεις με ταχύτητα c ισχύει x = y = ct – η γωνία που θα σχηματίζει κάθε γενέτειρα του κώνου με το οριζόντιο επίπεδο θα είναι γωνία 45⁰ . Εύκολα συμπεραίνεται ότι τα γεωμετρικά σημεία στο εσωτερικό της κωνικής επιφάνειας με την κορυφή προς τα κάτω θα αντιστοιχούν σε γεγονότα - αφίξεις μηνυμάτων που ταξιδεύουν με ταχύτητα μικρότερη από εκείνη των ηλεκτρομαγνητικών κυμάτων που είναι και ταχύτητα του φωτός. Συμπεραίνεται επίσης ότι τα γεωμετρικά σημεία έξω από τον κώνο δεν αντιστοιχούν σε γεγονότα του μέλλοντος διότι η άφιξη κάποιου αντίστοιχου μηνύματος θα απαιτούσε ταχύτητα μεγαλύτερη από εκείνη (c) του φωτός και τέτοια ταχύτητα δεν υπάρχει. Ο «πάνω κώνος» αναφέρεται σε ΓΕΓΟΝΟΤΑ ΤΟΥ ΜΕΛΛΟΝΤΟΣ, εφόσον έχουμε δεχθεί ότι η αρχή των αξόνων (το γεγονός της εκπομπής του σήματος) είναι το ΤΩΡΑ. Ο άλλος κώνος που βρίσκεται σε συμμετρική θέση και έχει κι αυτός ως κορυφή στην αρχή των αξόνων αντιστοιχεί σε γεγονότα του παρελθόντος.

Χώρος του Minkowski

Η βασική ΚΑΙΝΟΤΟΜΙΑ είναι η ΓΕΩΜΕΤΡΙΚΟΠΟΙΗΣΗ ΤΟΥ ΧΡΟΝΟΥ.

Δημιουργείται ο λεγόμενος «χώρος Minkowski», ένας 4-διάστατος διανυσματικός χώρος εφοδιασμένος με την «υπογραφή»

(-, +, +, +) όπως τη θεωρούν οι θεωρητικοί της Σχετικότητας ή

(+, -, - ,-) όπως τη θεωρούν οι φυσικοί των υψηλών ενεργειών

Για τους θεωρητικούς της Σχετικότητας οι τρεις άξονες είναι βαθμολογημένοι με τις χωρικές συντεταγμένες x, y , z, αλλά ο «τέταρτος άξονας» είναι βαθμολογημένος με τις τιμές ict όπου i η φανταστική μονάδα, ώστε και οι τέσσερις να έχουν τιμές σε κοινή μονάδα μέτρησης. Η απόσταση δύο σημείων - γεγονότων δίνεται από τη σχέση s² = x² + y² + z²- c²t²

Η γωνία που σχηματίζει η γενέτειρα του κώνου με όλους τους άξονες είναι πάντοτε 45⁰.

Κάθε γεωμετρικό σημείο του χώρου Minkowski αντιπροσωπεύει ένα γεγονός, δηλαδή ένα σημείο του χώρου σε κάποια συγκεκριμένη χρονική στιγμή.

Για ένα ακίνητο σωματίδιο η χωροχρονική διαδρομή είναι πάνω στον άξονα των χρόνων

Για ένα φωτόνιο η διαδρομή συμπίπτει με γενέτειρα του κώνου

Για κάθε κινούμενο σωματίδιο η διαδρομή είναι μια γραμμή στο εσωτερικό του κώνου.

ακίνητο σωματίδιο

κινούμενο σωματίδιο

φωτόνιο

Οι φυσικοί των υψηλών ενεργειών λένε τα ίδια πράγματα σε γλώσσα λίγο διαφορετική

Η ποσότητα d για την οποία d² = t²- ( x/c)² - ( y/c)² - ( z/c)² συνιστά το «χρονικό διάστημα» ανάμεσα σε δύο γεγονότα, ενώ η συντεταγμένη

της στον άξονα των χρόνων δεν μετρά τον χρόνο

παρά μόνο εάν το ρολόι μας είναι ακίνητο.

Σε άξονες it, x/c, y/c, z/c η ποσότητα αυτή d

σχετίζεται με την «απόσταση s» από την αρχή

των αξόνων με την d² = -s² . Με βάση αυτό τον

ορισμό η «απόσταση Minkowski» AC είναι

μακρύτερη από την αντίστοιχη μιας

σύνθετης πορείας AB+ BC και η μακρύτερη

από όλες τις κοσμικές γραμμές που ενώνουν

δύο γεγονότα είναι η ευθεία

Για περισσότερα

Το 4-διάνυσμα ενέργειας – ορμής και το 4-διάνυσμα χώρου - χρόνου