Ανδρέας Ιωάννου Κασσέτας

Μαθηματικές αναμνήσεις

Στα χρόνια της αθωότητας, στο γυμνασιολύκειο της γειτονιάς, το σύνολο «κορίτσια συμμαθήτριες» ήταν κενό σύνολο. Το σχολείο λεγόταν «έκτο Αρρένων Αθηνών». Τα μόνα δηλαδή θηλυκού γένους που κυκλοφορούσαν στις σχολικές αίθουσες και στη μεγάλη αυλή ήταν ένας αδέσποτος γάτος που τελικώς ήταν γάτα και τρεις καθηγήτριες, η μία των Γαλλικών και η άλλες δύο φιλόλογοι. Στη φαντασία του, εκτός από τα εκατοντάδες κορίτσια του γειτονικού Τρίτου θηλέων, θηλυκού γένους ήταν η απίστευτη Φυσική και μία εξίσου δυνατή κυρία, η «Μαθηματικά».

Ακομα και σήμερα τα Μαθηματικά τα φαντάζεται σαν μία ώριμη κυρία, ιδιαίτερα όμορφη για την ηλικία της. Πολύ μεγαλύτερη από τη Φυσική, είναι συνομήλικη με τη Φιλοσοφία δηλαδή δυόμισι περίπου χιλιάδων ετών, ίσως λίγο νεώτερη από την Ποίηση. Εκείνος είναι αρκετά νεώτερος και κάποτε «κόντεψε» να γίνει μαθηματικός αλλά την τελευταία στιγμή ομολόγησε την ερωτική του ιστορία με τη Φυσική, έτσι που ο γάμος με την ώριμη κυρία δεν έγινε ποτέ .

Εξυπακούεται ότι «η κυρία» , γέννημα της ανθρώπινης αφαιρετικής σκέψης, δεν υπήρχε πάντοτε. «Μια φορά κι έναν καιρό» υπήρχαν άνθρωποι που δεν είχαν ανακαλύψει ούτε τους αριθμούς.

Πέρασαν χιλιάδες χρόνια μέχρι να «διακρίνει» η ανθρώπινη αφαιρετική σκέψη ότι «ανάμεσα σε ένα ζευγάρι φασιανούς και σε ένα week end υπάρχει κάτι ΚΟΙΝΟ» . . . . . το ΔΥΟ . . ο ΑΡΙΘΜΟΣ ΔΥΟ έγραψε κάποτε ο Bernard Russel

Βέβαια τα βότσαλα είναι πολύ παλιότεροι κάτοικοι του πλανήτη από τον άνθρωπο.

υπήρχαν και πριν από τα Μαθηματικά. Χρειάζεσαι τρία βότσαλα για να φτιάξεις ένα ισόπλευρο τρίγωνο κι αν θες να φτιάξεις ένα μεγαλύτερο έτσι που κάθε βότσαλο να ισαπέχει από τα γειτονικά του χρειάζεσαι έξι, ενώ για ένα ακόμα μεγαλύτερο θες δεκαπέντε.

Με τα ινδοαραβικά σύμβολα είναι ο 3, ο 6, ο 10,

ο 15, ο 21, ο 28, ο 36, ο 45, ο 55 , o 66, o 78, . . .

οι πανάρχαιοι τριγωνικοί αριθμοί. Είναι μια υπόθεση που σε κείνον φέρνει ανεμάκι μνήμης παιδικής ενώ στην κυρία θυμίζει την εποχή που ήταν ακόμα νεαρή κοπέλα και τον παράξενο ελληνόφωνο εραστή της, τον Πυθαγόρα.

Χρειάζεσαι τέσσερα βότσαλα για να φτιάξεις ένα τετράγωνο. Για το αμέσως μεγαλύτερο τετράγωνο τα βότσαλα πρέπει να είναι 9 και για το επόμενο 16. Ο 4, ο 9, ο 16, ο 25, ο 36, ο 49, ο 64, ο 81 είναι οι λεγόμενοι τετραγωνικοί αριθμοί, τα «τετράγωνα» των ακεραίων αριθμών, οι «τέλεια τετράγωνα» .

Μπορείς μάλιστα να αποδείξεις ότι κάθε τετραγωνικός αριθμός είναι άθροισμα δύο διαδοχικών τριγωνικών.

4 = 1+3 9 = 3+6 16 = 10+6 25 = 10+15 36 = 15+21 . . . .

Θυμάται και το περίφημο τρίγωνο με τους αριθμούς που γνώρισε μικρός. Στις δύο πλευρές του υπάρχει μόνο ο αριθμός 1 οι άλλοι αριθμοί είναι βαλμένοι έτσι ώστε κάθε άθροισμα σε κάθε οριζόντια σειρά να είναι διπλάσιο από το αντίστοιχο της από πάνω σειράς. Συμβαίνει επίσης κάθε αριθμός να είναι το άθροισμα των δύο αμέσως από πάνω του.

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

1 6 15 20 15 6 1

Μπορεί επίσης να προβλέψει ότι οι οκτώ της αμέσως επόμενης σειράς είναι οι 1, 7, 21, 35, 35, 32, 7, 1 . «Είναι το περίφημο τρίγωνο του Pascal» του λέει η ώριμη κυρία. Ο Blaise Pascal παιδί θαύμα του 17^ου ήταν ένας από τους Γάλλους θαυμαστές της.

Το έργο Γεωμετρία.

Ανεβαίνει εδώ και πολλούς αιώνες σε όλα τα σχολεία του κόσμου με σκοπό να μυήσει σε «κάτι» που δεν υπάρχει στον κόσμο των πέντε αισθήσεων και των αντικειμένων με τα οποία μεγαλώσαμε τόσο εμείς όσο τα παιδιά της Σριλάνκα, του Λος Άντζελες, της Πολωνίας της Τουρκίας του Περού. Παίζεται με όργανα μια κιμωλία και ένα κατακόρυφο πρασινοπίνακα και ανεβαίνει πάντα με βασικούς πρωταγωνιστές τις δύο «φοβερές» γραμμές, την απολύτως ίσια ΕΥΘΕΙΑ και τον συμμετρικά στρογγυλό ΚΥΚΛΟ – με την ευθεία να τον αγγίζει ίσα ίσα σε ένα μόνο σημείο και

ο καθηγητής της Γεωμετρίας, ο κύριος

Κάρτσωνας – ένας πανύψηλος φοβοτρόμος

της τότε εφηβείας αργότερα χάθηκε μάθαμε

ότι κάπου στην επαρχία έγινε

Γυμνασιάρχης – να τη χαρακτηρίζει

εφαπτομένη , κι άλλοτε πάλι να τον κόβει

και να αφήνει μέσα του κομμάτια της που

ο κύριος Κάρτσωνας τα έλεγε χορδές.

Κι όταν δύο ευθείες είναι μόνες τους χωρίς

κύκλο μπορεί και να μην κόβουν η μία την άλλη οπότε ο καθηγητής τις χαρακτήριζε παράλληλες, - ήταν από τα λίγα που εκείνος μαθητής στο έκτο Αρρένων τα ήξερε πριν να τα πει ο καθηγητής κυκλοφορούσε στις γειτονιές της καθημερινής γλώσσας δεν ήταν όπως εκείνη η απίστευτη « εντός εναλλάξ».

Όταν οι ευθείες δεν ήταν παράλληλες σχημάτιζαν «γωνία» και ο κύριος Κάρτσωνας δεν του επέτρεπε τη λέει γωνιά να βάζει δηλαδή τον τόνο στο άλφα, όπως έκανε με την αγαπημένη του γωνιά στο παιδικό του δωμάτιο ή με εκείνη στο «γωνιά γωνιά σε καρτερώ, γωνιά γωνιά σε ψάχνω» που έλεγε ο Γρηγόρης

Μπιθικότσης.

Οι γωνίες της Γεωμετρίας διέφεραν από τις «γωνιές» που τονίζονταν στο έψιλον Εκείνες τονίζονταν στο γιώτα. Ήταν οι «γωνίες» και σχεδόν όλες κυκλοφορούσαν με ονόματα της καθαρεύουσας ή της αρχαίας ελληνικής, ανάμεσά τους η πιο «σωστή» απ΄ όλες η ΟΡΘΗ, σαν εκείνη στην άκρη του τραπεζιού ή την άλλη στις άκρες των τετραδίων . Η ορθή, η 90 μοιρών ήταν και ένα όριο έτσι που κάθε μικρότερη από αυτή ήταν μια ΟΞΕΙΑ – το θηλυκό του οξύς, το ουδέτερο το συνάντησε αργότερα ως θειικό ή νιτρικό στη Χημεία – και κάθε μεγαλύτερη από αυτήν ήταν μια ΑΜΒΛΕΙΑ. Κι ακόμα αξέχαστες γωνίες ήταν η εγγεγραμμένη – ως μετοχή του ρήματος εγγράφομαι την έλεγε στο μάθημα των αρχαίων ελληνικών - και η επίκεντρη με το προσωπικό της τόξο. Μαζί και εκείνη η αξέχαστη «διχοτόμος» - κάθε γωνία θα μπορούσε να έχει τη διχοτόμο της - αλλά και μερικά ζευγάρια που έχουν αφήσει ίχνη στις περιοχές της μνήμης , τα συνάντησε στο Γυμνάσιο, εκπεμπόμενα από το στόμα του κυρίου Κάρτσωνα, με ονόματα σκληρής καθαρεύουσας, οι «κατά κατακορυφήν», οι «εντός εναλλάξ», οι «εντός εκτός και επί τα αυτά», οι «παρά την βάση ισοσκελούς τριγώνου», οι παραπληρωματικές και συμπληρωματικές, οι μόνες που τις είχε καταλάβει από την αρχή.

Η άλλη δυνατή του ανάμνηση είναι τα τρίγωνα, ισοσκελή, σκαληνά, ισόπλευρα, ορθογώνια, ορθογώνια και ισοσκελή καθένα τους με μια ειδική εσωτερική αναπαράσταση στον εσωτερικό του σύμπαν και η φωνή του κυρίου Κάρτσωνα με τόνο που δεν σήκωνε αντίρρηση ακόμα κι αν υπέβαλε την κλασική ερώτηση « πότε δυο τρίγωνα είναι ίσα», εκείνος έπρεπε να επιστρατεύσει κάθε ικμάδα συγκέντρωσης και να απαγγείλει το σχετικό ποίημα «πρώτον όταν έχουν και τις τρεις πλευρές ίσες, δεύτερον όταν έχουν δύο πλευρές και την περιεχόμενη γωνία και τρίτο όταν έχουν ίσες μία πλευρά και τις δύο προσκείμενες γωνίες».

Εκείνο πάντως που του είχε κάνει - και του κάνει ακόμα και τώρα- ιδιαίτερη εντύπωση είναι ότι

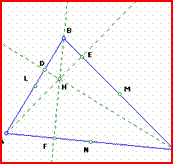
ΚΑΙ ΤΑ ΤΡΙΑ ΥΨΗ ενός οποιουδήποτε τριγώνου θα συναντηθούν σε κάποιο σημείο

ΚΑΙ ΟΙ ΤΡΕΙΣ ΔΙΑΜΕΣΟΙ οποιουδήποτε τριγώνου συναντώνται σε ένα κοινό σημείο

ΚΑΙ ΟΙ ΤΡΕΙΣ ΔΙΧΟΤΟΜΟΙ των γωνιών κάθε τριγώνου συναντώνται σε κάποιο σημείο

κέντρο του εγγεγραμμένου κύκλου, το έλεγε ο συμμαθητής Γιώργος Γ. , ο λεγόμενος Γεωμέτρης.

ΚΑΙ ΟΙ ΤΡΕΙΣ ΜΕΣΟΚΑΘΕΤΟΙ στις πλευρές οποιουδήποτε τριγώνου συναντώνται και οι τρεις σε κάποιο άλλο χαρακτηριστικό σημείο, κέντρο του περιγεγραμμένου κύκλου, το έλεγε ο κύριος.

αλλά και το ΣΟΒΑΡΟΤΕΡΟ ότι «όλα αυτά μπορούσαν ΝΑ ΑΠΟΔΕΙΧΘΟΥΝ ΛΟΓΙΚΑ». Ε! αυτό τον γοήτευε και τον γοητεύει ακόμα.

Ποιο είναι το βαθύτερο μυστικό όλης αυτής της ιστορίας;

Γιατί οι δύο διάμεσοι θα συναντηθούν κάπου, εύκολα μπορούσε να διακρίνει ότι δεν είναι παράλληλες-

αλλά ΚΑΙ η τρίτη; Ξεκινάει από την κορυφή και

«σημαδεύει» το μέσον της απέναντι πλευράς.

Τι ήταν αυτό που την ανάγκαζε ΛΟΓΙΚΑ να περνάει

από το σημείο της συνάντησης των άλλων δύο;

Ο κύκλος του Euler

A circle is a happy thing to be--

Think how the joyful perpendicular

Erected at the kiss of tangency

Must meet my central point, my avaton.

And lovely as I am, yet only 3

Points are needed to determine me.

Christopher Morley (1890-1957)

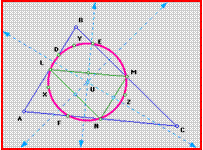
Προτελευταία τάξη, Πρακτικό, και ο Κύκλος του Euler η περιφέρεια των εννέα σημείων, μία

από τις πιο γοητευτικές συναντήσεις του με την ευκλείδεια Γεωμετρία. Μα είναι δυνατόν και τα ΕΝΝΕΑ ΣΗΜΕΙΑ να ανήκουν στην ίδια περιφέρεια; Και αυτό να συμβαίνει σε όλα τα τρίγωνα του κόσμου; Και ποιος είναι αυτός

ο Euler που προφέρεται «Όιλερ»;

Τον φανταζόταν στην Ελβετία στα 1700 τόσο –

σε μικρή ηλικία - να σχεδιάζει ένα τρίγωνο και

να του δίνει όνομα.

Πήγε να το επαναλάβει κι εκείνος

αλλά στο δικό του τώρα του 21ου αιώνα

Σχεδίασε το τρίγωνο και του έδωσε το όνομα.

Το είπε ABC Στο μέσον καθεμιάς από τις τρεις

πλευρές έδωσε ένα όνομα ένα γράμμα του αλφαβήτου.

Το σημείο L, το σημείο M και το σημείο Ν.

Από κάθε μια από τις τρεις κορυφές έφερε την κάθετο

στην απέναντι πλευρά , το ΥΨΟΣ όπως λέγεται

στη γλώσσα της Γεωμετρίας.

Στα σημεία που τέμνει κάθε ύψος την πλευρές έδωσε

όνομα. Τα είπε E, D και F. Το σημείο που

συναντώνται τα τρία ύψη, στη γλώσσα της

Γεωμετρίας ορθόκεντρο, το είπε Η. Έδωσε

τέλος όνομα και στο μέσον των ευθυγράμμων

τμημάτων που συνδέουν το ορθόκεντρο με κάθε

κορυφή. Αυτή τη φορά χρησιμοποίησε κεφαλαία

γράμματα από το τέλος του αλφαβήτου. Τα είπε

X, Y και Z. Είχε ήδη δώσει όνομα σε εννέα

σημεία. Υποστήριξε ότι και τα εννέα σημεία

L , M, Ν, E, D, F, X, Y και Z δηλαδή

τα τρία μέσα των πλευρών,

τα τρία σημεία προβολές της κάθε κορυφής στην απέναντι πλευρά και τα τρία μέσα των αποστάσεων ορθόκεντρο κορυφή ΑΝΗΚΟΥΝ – και τα εννέα - στον ίδιο κύκλο

Προσπάθησε να θυμηθεί το «πώς προσδιορίζεται το κέντρο του κύκλου» αλλά οι δεκαετίες από το Πρακτικό του έκτου Αρρένων μέχρι σήμερα ήταν πια τόσες που η μνήμη δήλωνε άρνηση. Κατέφυγε στην αγκαλιά του Internet και το ξαναείδε:

Για να βρούμε το κέντρο του κύκλου σχεδιάζουμε

το τρίγωνο των τριών μέσων των πλευρών L , M, Ν

και βρίσουμε το κέντρο U του περιγεγραμμένου κύκλου

του τριγώνου αυτού. Το σημρίο U θα είναι και

το ζητούμενο κέντρο του κύκλου του Euler.

η πρώτη του αλγεβρική εξίσωση

ήταν βέβαια η «πρώτου βαθμού»

αx+β = 0

όταν τη γνώρισε «εκείνος» 13 ετών εκείνη αρκετών αιώνων.

Η λύση της ήταν ένα ποίημα που το είχε αποστηθίσει

απαλοιφή των παρονομαστών εκτέλεση των πράξεων

χωρισμός των γνωστών από τους αγνώστους

-έτσι που οι άγνωστοι να βρεθούν οπωσδήποτε ΑΡΙΣΤΕΡΑ -

αναγωγή ομοίων όρων αx = -β

διαίρεση με τον συντελεστή του αγνώστου

και επιτέλους ☺ η λύση x = -β/α

η πρώτη του αλγεβρική ταυτότητα

(α+β)² = α² + 2αβ + β²

την είχε μάθει «απ’ έξω» όπως και την άλλη την

(α+β) (α-β) = α² - β²

πάντα του έκαναν εντύπωση οι λέξεις. Έψαχνε και για τις σημασιες τους αλλά και για την καταγωγή τους. Στην προκειμένη περίπτωση ο όρος ΤΑΥΤΟΤΗΤΑ σήμαινε κάποια ισχυρή ισότητα, σήμαινε ότι το άθροισμα α²+2αβ+β² είναι το ΙΔΙΟ ΠΡΑΓΜΑ με το (α+β)² ή με το (α+β) (α+β) και μας εξυπηρετεί να το θυμόμαστε ή να αναγνωρίζουμε το ένα βλέποντας το άλλο

Δεν πρόλαβε να αναρωτηθεί για το (α+β)³ . Γρήγορα υποχρεώθηκε να μάθει απέξω ότι είναι ίσο με άθροισμα τεσσάρων όρων α³ + 3α²β + 3αβ² + β³

Σκέφτηκε μάλιστα ότι εάν βάζει αντί για β το –β θα έχει και τις ταυτότητες για το (α-β)² καθώς και για το (α-β)³ και επειδή το «να ξέρει» τις ταυτότητες ήταν τελικά μόνο θέμα ΜΝΗΜΗΣ – κάτι δηλαδή που δεν εμπεριέχεται στο « γιατί ΜΑΘΗΜΑΤΙΚΑ » - υπέθεσε ότι αρκούσε η σκέψη «αντί για β το –β» για να ξέρει και τις δύο ταυτότητες

την (α-β)² =α²-2αβ+β² και την (α-β)³ = α³ - 3α²β + 3αβ² -β³

Πρόσεξε επίσης και τους αριθμητικούς συντελεστές στη μία και στην άλλη ταυτότητα. Στη μία ήταν οι αριθμοί 1,2,1 ενώ στην άλλη ήταν οι 1,3,3,1 . Η σειρά του έφερε στο μυαλό το ΤΡΙΓΩΝΟ του Pascal και αναρωτήθηκε μήπως στην (α-β)⁴ = . . . οι όροι είναι πέντε και οι συντελεστές ήταν οι 1, 4, 6,4, 1 οι ακέραιοι δηλαδή της επόμενης σειράς του τριγώνου. Όσο για τους εκθέτες είχε προβλέψει ότι θα ελαττώνεται η δύναμη του άλφα και θα αυξάνεται η δύναμη του βήτα. Έκανε τις πράξεις και πράγματι φάνηκε ότι είχε δίκιο. Οι πράξεις οδηγούσαν στο (α-β)⁴=α³ +4α³β + 6α²β² + 4αβ³+ β⁴.Το ανάπτυγμα είχε πέντε όρους και οι συντελεστές ήταν εκείνοι που «έδειχνε» το τρίγωνο.

Ήταν πια βέβαιος ότι «ξέροντας να φτιάχνει το ΤΡΙΓΩΝΟ του Pascal μπορούσε να ξέρει οποιαδήποτε ταυτότητα (α-β)^ν».

Αργότερα θα μάθαινε ότι το ΤΡΙΓΩΝΟ του Pascal μπορούσε να το αξιοποιήσει και για βρίσκει «τον ΑΡΙΘΜΟ των ΣΥΝΔΥΑΣΜΩΝ ν πραγμάτων από τα οποία

παίρνουμε κάθε φορά ρ πράγματα».

η πρώτη του γνωριμία με το πανάρχαιο «ελληνικό» θεώρημα της Γεωμετρίας . Μια σχέση

ανάμεσα στα μήκη των πλευρών όλων των

ορθογωνίων τριγώνων του Σύμπαντος α² = β² + γ²

την είχε μάθει «απ’ έξω»

όταν άρχισε να εφαρμόζει το πυθαγόρειο θεώρημα, εντύπωση του έκανε η τριάδα «3, 4 ,5» ως μήκη πλευρών ορθογωνίου τριγώνου. Δοκίμασε και με την τριάδα 2, 3, 4 για να διαπιστώσει εύκολα ότι δεν μπορούσε να είναι πλευρές ορθογωνίου τριγώνου. Το ίδιο έγινε και με την τριάδα 4, 5 ,6. Αναρωτήθηκε «ποιες άλλες τριάδες φυσικών αριθμών θα μπορούσαν να είναι πλευρές ορθογωνίου τριγώνου» και η πρώτη βέβαια επιλογή ήταν «όλα τα πολλαπλάσια των «3, 4 ,5» δηλαδή οι τριάδες «6, 8 ,10» «9, 12, 15» «15, 20 ,25» «18, 24, 30» και οι υπόλοιπες. Αναρωτήθηκε εάν υπάρχουν άλλες τριάδες εκτός από αυτές. Σε γλώσσα άλγεβρας τριάδες φυσικών αριθμών α, β, γ, που ικανοποιούν τη σχέση α² + β² = γ² . Και τυχαία διέκρινε την τριάδα «12, 5, 13» άρα και τα πολλαπλάσιά της την «24, 10, 26» την «36, 15, 39» και τις υπόλοιπες. Αναρωτήθηκε πώς θα μπορούσε να αναζητήσει τις άλλες τριάδες αλλά δεν το κατάφερνε και το άφησε.

η πρώτη του τριγωνομετρία ημ²x + συν²x = 1

την είχε μάθει «απ’ έξω»

αργότερα

η επόμενη αλγεβρική του εξίσωση,

η «δευτεροβάθμια»

αx²+βx+γ = 0 x = (-β∓ +ÖΔ)/2α

και η γνωριμία του με την ποσότητα που κυκλοφορούσε ως κεφαλαίο Δ

κι εκείνος έπρεπε να μπορεί να τη «διακρίνει»

Για κάποιον άγνωστο λόγο το όνομά της

ήταν η μετοχή του ρήματος ΔΙΑΚΡΙΝΩ

και αν «εκείνη» ήταν αρνητική η εξίσωση ΔΕΝ είχε λύσεις

Αργότερα έμαθε πως ακόμα κι αν «εκείνη» ήταν αρνητική υπήρχαν κάποιες λύσεις. Ήταν αριθμοί- τέρατα που δεν τους χωρούσε η φαντασία του.

η βασιλοπούλα ΣΥΝΑΡΤΗΣΗ

και εν τω μεταξύ - αρκετά νωρίς - οι μαθηματικοί του σχολείου του είχαν μιλήσει για την έννοια ΣΥΝΑΡΤΗΣΗ - μια από τις βασιλοπούλες των μαθηματικών – και για την εντυπωσιακή ιδέα ενός Γάλλου του 17^ου αιώνα πει ότι κάθε ΣΥΝΑΡΤΗΣΗ μπορεί να έχει μια δική της γεωμετρική ΕΙΚΟΝΑ, τη γραφική παράσταση.

Το όνομα του Γάλλου άλλοτε το άκουγε περίπου ελληνικό, δηλαδή

«Καρτέσιος», κι άλλοτε με τη γαλλική εκδοχή του ως «Descartes» που προφέρεται «Ντεκάρτ» .

Κάθε πρωτοβάθμια συνάρτηση μπορούσε

να κυκλοφορεί είτε με το αλγεβρικό της

ρούχο του στυλ y = ax + β είτε

με τη γεωμετρική της περιβολή

ως ευθεία γραμμή.

Μια δευτέρου βαθμού συνάρτηση μπορούσε να κυκλοφορεί είτε με το αλγεβρικό της ρούχο του στυλ y = ax² βx + γ είτε με τη γεωμετρική της περιβολή ως καμπύλη «παραβολή»

Κάπου εκεί διαπίστωσε και ότι η συνάρτηση με το αλγεβρικό ένδυμα y = aημx όταν φόραγε

το ρούχο της γραφικής

παράστασης γινόταν

η ΩΡΑΙΟΤΕΡΗ

ΚΑΜΠΥΛΗ του ΚΟΣΜΟΥ

Είχε ήδη φανταστεί «το μπαρ με τις καμπύλες» στο οποίο σύχναζαν οι δύο πανάρχαιες αγαπημένες του Ευκλείδη, η χωρίς την παραμικρή καμπυλότητα ΕΥΘΕΙΑ και η φοβερή εκείνη δημοκρατία σημείων που την φώναζαν ΚΥΚΛΟ, η ΕΚΘΕΤΙΚΗ που άλλοτε εμφανιζόταν ως με το ηθικό ανεβασμένο ως αύξουσα και άλλοτε ως φθίνουσα που συνήθιζε να παραγγέλλει τζιν με λεμόνι και να κοιτάζει τη ΛΟΓΑΡΙΘΜΙΚΗ στα μάτια, η ασύγκριτης ομορφιάς ημιτονοειδής που τη φώναζαν και ΑΡΜΟΝΙΚΗ κι άλλες ιδιόμορφες και με μικρότερη φήμη όπως η κυκλοειδής και η καρδιοειδής αλλά και οι 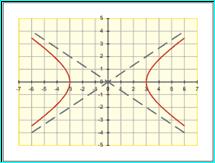τρεις μεγάλης ηλικίας ελληνίδες θυγατέρες του

του Απολλώνιου από τη συνάντησή του με την κυρία Μαθηματικά,

η ΥΠΕΡΒΟΛΗ η ΠΑΡΑΒΟΛΗ και η ΕΛΛΕΙΨΗ.

Στο μεταξύ τα πρωινά στο σχολείο

μάθαινε κι άλλα που θα του έμεναν αξέχαστα

ημ(α+β) = ημασυνβ + ημβσυνα

ln(ab) = lna+ lnb

1 + 2 + 3 + 4 + 5 . . . . +ν = ½(ν+1)ν

α + αω + αω² + αω³+ . + αω^ν = (αω^ν- α)/(ω-1)

1²+ 2² + 3² + 4²+ 5² + . . . ν² = ¹/₆ ν ( ν+1 ) (2ν+1)

και μπορεί βέβαια τα χρόνια μέσα στις σχολικές αίθουσες να έτρεχαν με τη δική τους μικρή ταχύτητα αλλά

οι αιώνες είχαν ήδη κυλήσει και η κυρία Μαθηματικά είχε εμπλουτιστεί με την ευρωπαική παρέμβαση. Τα ευρωπαϊκά Μαθηματικά είχαν ωριμάσει τόσο που ήταν δύσκολο να διδαχθούν ακόμα και σε εκείνον έναν νεαρό μαθητή του εικοστού αιώνα.

Ήταν δύσκολο για τους καθηγητές των μαθηματικών του Γυμνασιολυκείου του 20^ου αιώνα να διδάξουν την ταυτότητα που είχε παρουσιάσει 350 χρόνια νωρίτερα

στην Αγγλία o Isaac Newton

(α+β)ⁿ = αⁿ + n_/1! α^n-1β + n(n-1)_/2! α^n-2β² + n(n-1) (n-3)_/3! + . .+ n(n-1) . . 2_{/(n-1)! a}αβ^n-1 + βⁿ

ενώ την ίδια εποχή - τέλος του 17^ου αιώνα - στη Γερμανία

έκαναν τη «δική» τους εμφάνιση οι έννοιες

ΠΑΡΑΓΩΓΟΣ και ΟΛΟΚΛΗΡΩΜΑ

ίδιες με εκείνες που είχε επινοήσει ο Newton

αλλά με έναν δικό τους συμβολισμό

αυτόν με τον οποίο «εκείνος»

θα τις προσέγγιζε με δέος στην στα πρώτο έτος στο Πανεπιστήμιο

d(ax²)/dx = 2ax òaxdx = ½ax²

με την υπογραφή Wilhelm Leibniz , 1684

αλλά και οι βασικοί κανόνες

d(x^ν) =νx^ν-1dx d(xy) =xdy +ydx d(x/y)=(ydx- xdy)/y²

με την υπογραφή πάντα του Leibniz

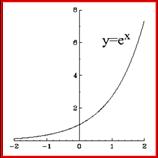
Στο μεταξύ εκείνος είχε μάθει και το μεγάλο μυστικό

της εκθετικής y = e^x .

Ότι εάν την παραγωγίσεις θα διατηρηθεί αναλλοίωτη.

Στη γλώσσα των μαθηματικών η πρώτη παράγωγος

της y = e^x είναι e^x και στη γλώσσα των συμβόλων

του Leibniz dy/dx = y.

Όσο για την άλλη εκθετική τη φθίνουσα y = e^-x

θα χρειαστεί να την παραγωγίσεις δύο φορές για ξαναβρείς την αρχική. d²y/dx² = y.

Εκείνος δοκίμασε να παραγωγίσει και την y = ημx την ωραιότερη καμπύλη του κόσμου και είδε ότι με δύο παραγωγίσεις ξανάπαιρνε την αρχική της μορφή.

Ήταν τότε που επινόησε και εκείνη την ιστορία με το μπαρ.

Στο μπαρ που συχνάζουν οι καμπύλες ανοίγει απότομα η πόρτα και κάνει την εμφάνισή του ο παραγωγός. «Ποια θα παραγωγίσω σήμερα;» Η παραβολή τρέχει να κρυφτεί γιατί εάν την παραγωγίσει θα γίνει ευθεία,

η ευθεία y = 5x αφήνει το ποτό της και το βάζει στα πόδια, βλέπεις εάν την παραγωγίσει θα γίνει y = 5

μια συνάρτηση δηλαδή που δεν θα είναι συνάρτηση και ο πανικός απλώνεται σε όλες.

Η μόνη που συνεχίζει να πίνει το τζιν της είναι η ΕΚΘΕΤΙΚΗ y = e^x . «Ά να χαθείς ηλίθιε» του λέει και τον κοιτάζει με ύφος cool. «Όσες φορές και να με παραγωγίσεις εγώ θα συνεχίσω να είμαι όπως ήμουνα»

τον 17^ο αιώνα η κυρία Μαθηματικά

ένιωσε ιδιαίτερες συγκινήσεις όταν

η θυγατέρα Τριγωνομετρία

από τη σκιά της Αστρονομίας

στην οποία είχε περάσει τα παιδικά της χρόνια ,

- είχε λίγο βοηθήσει και η τροφός Γεωγραφία στην ενηλικίωσή της -

τώρα πια - έτος 1722 και Abraham de Moivre-

(συνφ + iημφ)ⁿ = συνnφ + iημnφ

βρέθηκε στην αγκαλιά της απαιτητικής Ανάλυσης

Στο μεταξύ στη ζωή της κυρίας Μαθηματικά είχε μπει

η έννοια ΔΥΝΑΜΟΣΕΙΡΑ.

Συνάρτηση του x αλλά και άθροισμα απείρων όρων

καθένας από τους οποίου περιείχε μια δύναμη του x .

f (x) = α₀ + α₁x + α₂x² + α₃x³ + α₄x⁴ + . . .

Αυτό το «ΑΘΡΟΙΣΜΑ ΑΠΕΙΡΩΝ ΟΡΩΝ» ποτέ του δεν το κατάλαβε. Ήξερε ότι για να οικοδομηθεί η έννοια ΑΘΡΟΙΣΜΑ πρέπει να είναι γνωστό το πόσοι είναι οι όροι. «ΑΘΡΟΙΣΜΑ ΑΠΕΙΡΩΝ ΟΡΩΝ» τι να σημαίνει άραγε; Η βαθύτερη σημασία αυτής της έννοιας ήταν ασύλληπτη τουλάχιστον για εκείνον. Ωστόσο το χρησιμοποιούσε σαν εργαλείο .

Και μπορεί εκείνος να συναντήθηκε μαζί της στα χρόνια τα φοιτητικά αλλά η έννοια «έπαιζε» στο έργο Μαθηματικά από την αυγή του 18^ου αιώνα

στην Αγγλία, το 1715, o Brooke Taylor

f (x) = f(a) + f΄(a)( x-a ) + f^(ν-1)(a)( x-a )^ν-1/ (ν-1)! + . .

και στη συνέχεια , το 1742, ο Σκωτσέζος Colin Maclaurin

f (x) = f(0) + f’(0) x + f’’(0) x²/ 2! + f’’’(0)x³/ 3! + . .

Ήταν εντυπωσιακό. Οι πιο διάσημες από τις συναρτήσεις έκαναν μία απρόβλεπτη επανεμφάνιση. Καθεμιά τους εμφανιζόταν ως ΔΥΝΑΜΟΣΕΙΡΑ

η «e εις την x»

e^x = 1 + x + x²/2! + x³/3! + x⁴/ 4! + . .

e = 1 + 1/1! + 1/2! + 1/3! + 1/4! + . = 2, 718254

με την υπογραφή Colin Maclaurin και Leonhard Euler

είχε εν τω μεταξύ προηγηθεί – Nicolaus Mercator 1668, Logarithmotechnia –

η «λογάριθμος» ln(1 + x) = x - x²/2 + x³/3 - x⁴/4 + ...

η «ημίτονο x»

ημx = x – x³/3! + x⁵/5! – x⁷/7! + . .

με την υπογραφή Colin Maclaurin και Leonhard Euler

η «συνημίτονο x»

συνx = 1 – x²/2! + x⁴/4! – x⁶/6! + . .

με την υπογραφή Colin Maclaurin και Leonhard Euler

Είχε ήδη κάνει την εμφάνισή του στο προσκήνιο

o Leonhard Euler

το 1755 αφού πίστεψε ότι η έννοια δυναμοσειρά μπορεί να ισχύει και για τις μιγαδικές συναρτήσεις οδηγήθηκε στη διάσημη – κυκλοφορεί και σε ελβετικό γραμματόσημο -

e^ix = cosx + isinx

Για εκείνον που ήταν φοιτητής του 20^ου αιώνα ήταν ένα ακόμα απρόβλεπτο ραντεβού τριών «πλασμάτων» της ανθρώπινης αφαιρετικής σκέψης που τον άφησε άφωνο.

Ο «φανταστικός γιωτ i », ο ασύλληπτος «e» και οι μεγαλωμένοι στη σκιά της αστρονομίας

«ημίτονο» και «συνημίτονο» σε μία εντυπωσιακή συγκατοίκηση.

Ο Euler. Ήξερε ότι εάν τροφοδοτούσε τη συνάρτηση y = e^x με τους συνήθεις

πραγματικούς αριθμούς θα έχουμε ένα γράφημα που αυξάνεται ταχύτατα.

Όταν όμως τροφοδότησε τη συνάρτηση με μιγαδικούς στην y = e^ix διέκρινε ένα απροσδόκητο αποτέλεσμα. Αντί για αυξανόμενο διάγραμμα παρουσιάστηκαν ΚΥΜΑΤΑ, ανάλογα με αυτά που περιγράφουν τη διάδοση του ήχου.

και «εκείνος» στα χρόνια τα φοιτητικά θα είχε διάφορες συναντήσεις μαζί της όπως τότε που χρειάστηκε να καταλάβει το «πώς προκύπτει η οικοδόμηση της εξίσωσης Schröndinger, τότε που κατάλαβε ότι η τιμή της κυματοσυνάρτησης Ψ ήταν ένας μιγαδικός αριθμός.

( το κείμενο αφιερώνεται σε έναν μαθητή του «σήμερα» , τον μαθητή της Β΄ Λυκείου Νικόλα Πρωιμάκη )

Ανδρέας Ιωάννου Κασσέτας

οι ΑΡΙΘΜΟΙ