Ανδρέας Ιωάννου Κασσέτας
![]()
οι ακέραιοι
- οι πρώτοι
- οι τέλειοι
- οι τριγωνικοί
- οι πυθαγόρειες τριάδες
- οι φιμπονάτσι
οι πρώτοι
Ο «6»
είναι «γινόμενο» του
«2» και του «3», «γίνεται» από
τον 2 και τον 3. Ο «30» «γίνεται» από τον
2, τον 3 και τον 5, ενώ ο 17 «δεν
γίνεται» από κάποιους άλλους αριθμούς. Ο «17» είναι ΠΡΩΤΟΣ , όπως και ο 13,
ο 5, ο 7 και ο 11 , όπως και
κάθε ακέραιος που δεν έχει διαιρέτη εκτός φυσικά από τον εαυτό του και από τον
1. Οι ΠΡΩΤΟΙ είναι οι «δομικοί λίθοι» των (ακέραιων) αριθμών και αυτό είναι
κάτι που το διέκριναν οι Έλληνες όταν διαπίστωσαν ότι κάθε αριθμός μπορεί να «γίνει» από πρώτους αριθμούς.
Όπως οι χημικοί αγωνίστηκαν να προσδιορίσουν τα βασικά στοιχεία
της ύλης και κατέληξαν στα 92 διαφορετικά άτομα, οι Έλληνες μαθηματικοί έκαναν
μια καλή αρχή βλέποντας τους ΠΡΩΤΟΥΣ
κάτι σαν « ΑΤΟΜΑ της ΑΡΙΘΜΗΤΙΚΗΣ » σαν δομικούς δηλαδή λίθους όλων των αριθμών.
Ποιοι είναι οι πρώτοι αριθμοί;
Εύκολη η απάντηση για τους «μικρούς» αριθμούς, δύσκολη έως αδύνατη για
τους πολύ μεγάλους . Ας αρχίσουμε όμως από τους μικρούς. Κατ’ αρχήν κανένας
πρώτος δεν μπορεί είναι άρτιος. Στην περιοχή των μονοψήφιων οι πρώτοι είναι τέσσερεις, ο 2, ο 3, ο 5
και ο 7. Στη δεύτερη δεκάδα είναι επίσης τέσσερεις, ο 11, ο 13, ο 17, ο 19 ενώ
στην τρίτη δεκάδα είναι τρεις, ο 23, ο 27 και ο 29 και στην τέταρτη ο 31, ο 37
και ο 39 και στην πέμπτη ο 41, ο 43 και ο 47. Στους πρώτους δηλαδή 50 ακέραιους
οι ΠΡΩΤΟΙ είναι δεκαπέντε αριθμοί.
οι τέλειοι
Ο Πυθαγόρας πίστευε ότι ορισμένοι αριθμοί, όπως ο 6,
πρέπει να θεωρούνται «τέλειοι». Τέλειος λέγεται
κάθε αριθμός ο οποίος είναι ίσος
με το άθροισμα των διαιρετών του. Ο 6 είναι ΤΕΛΕΙΟΣ διότι είναι ίσος με το
άθροισμα των 1, 2 και 3 και οι 1,2,3 είναι οι τρεις διαιρέτες του (6=1+2+3) . Αυτό
δεν συμβαίνει ούτε με τον 5, ούτε με τον 7 ούτε με τον 8 ούτε με κανένα άλλο
μονοψήφιο. Για να βρούμε τον επόμενο τέλειο αριθμό χρειάζεται σχετική υπομονή διότι επόμενος τέλειος είναι ο 28
= 1+2+3+4+5+6+7 . Εάν δε θελήσουμε να αναζητήσουμε τον επόμενο τέλειο αριθμό θα
χρειαστεί μεγάλη υπομονή. Είναι ο αριθμός 496 = 1+2+3+4+5+6+ . . . +30 +31. Όσο
για τον επόμενο, εάν δεν βρούμε άλλον τρόπο για την αναζήτηση, ας το αφήσουμε
καλύτερα.
Μια από τις ιδέες του Πυθαγόρα ήταν και ότι η τελειότητα
σχετίζεται με τις δυνάμεις του 2. Παρατήρησε δηλαδή ότι όλες οι δυνάμεις του
αριθμού 2 αποτυγχάνουν μόλις στο να είναι τέλειοι αφού το άθροισμα των διαιρετών τους είναι μικρότερο ΜΟΝΟ κατά μία
μονάδα από τους ίδιους .
Ας δούμε τον 22
= 4 Διαιρέτες οι 1,2 Άθροισμα των διαιρετών = 3
23 = 8
Διαιρέτες οι 1,2,4
Άθροισμα των διαιρετών = 7
24 = 16
Διαιρέτες οι 1,2,4,8
Άθροισμα των διαιρετών = 15
25 = 32
Διαιρέτες οι 1,2,4,8,16 Άθροισμα των διαιρετών =
31
26 = 64
Διαιρέτες οι 1,2,4,8,16,32 Άθροισμα των διαιρετών =
63
Πολλούς αιώνες αργότερα ο Ευκλείδης το διατύπωσε πιο εκλεπτυσμένα.
Ανακάλυψε ότι οι όλοι οι τέλειοι αριθμοί είναι πάντοτε γινόμενο μιας δύναμης του
2 επί την επόμενη δύναμη του 2 μείον 1
6 = 21.(22-1 ) 28 = 22.(23-1
) 496 = 23.(24-1
)
Μπορούμε τώρα να βρούμε τον – μετά τον 496 – αμέσως μεγαλύτερο
τέλειο αριθμό. Είναι ο 8128 = 24.(25-1) . Στην εποχή μας, με τη βοήθεια των
υπολογιστών, έχουμε βρει παραδείγματα τέλειων αριθμών με περισσότερα από
130.000 ψηφία. Ο « 2216091.(
2216091-1) » αποτελεί ένα χαρακτηριστικό παράδειγμα.
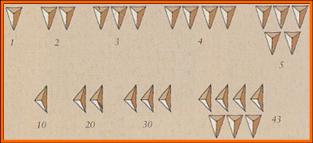
οι τριγωνικοί
 Χρειάζεσαι τρία βότσαλα για να
φτιάξεις ένα τρίγωνο
Χρειάζεσαι τρία βότσαλα για να
φτιάξεις ένα τρίγωνο
κι αν θες να φτιάξεις ένα μεγαλύτερο
έτσι που κάθε βότσαλο να ισαπέχει από τα
γειτονικά του χρειάζεσαι έξι, ενώ για ένα ακόμα
μεγαλύτερο θες δεκαπέντε.
Με τα ινδοαραβικά σύμβολα
είναι ο 3, ο 6, ο 10, ο 15, ο 21, ο 28, ο 36, ο 45, ο 55 . . . οι
πανάρχαιοι τριγωνικοί αριθμοί.
οι πυθαγόρειες τριάδες
Όταν άρχισε να εφαρμόζει το
πυθαγόρειο θεώρημα, εντύπωση του έκανε η τριάδα «3, 4 ,5» ως μήκη πλευρών ορθογωνίου τριγώνου. Δοκίμασε και με την
τριάδα 2, 3, 4 για να διαπιστώσει εύκολα ότι δεν μπορούσε να είναι πλευρές ορθογωνίου
τριγώνου. Το ίδιο έγινε και με την τριάδα 4, 5 ,6. Αναρωτήθηκε «ποιες άλλες
τριάδες φυσικών αριθμών θα μπορούσαν να είναι πλευρές ορθογωνίου τριγώνου» και η πρώτη βέβαια επιλογή ήταν «όλα τα
πολλαπλάσια των «3, 4 ,5» δηλαδή οι τριάδες «6, 8 ,10» «9, 12, 15» «15, 20 ,25»
«18, 24, 30» και οι υπόλοιπες. Αναρωτήθηκε εάν υπάρχουν άλλες τριάδες εκτός από
αυτές. Σε γλώσσα άλγεβρας τριάδες
φυσικών αριθμών α, β, γ, που ικανοποιούν τη σχέση α2 + β2
= γ2 .
Και τυχαία διέκρινε την τριάδα «12, 5, 13» άρα και τα πολλαπλάσιά
της την «24, 10, 26» την «36, 15, 39»
και τις υπόλοιπες. Αναρωτήθηκε πώς
θα μπορούσε να αναζητήσει τις άλλες τριάδες αλλά δεν το κατάφερνε και το άφησε.
Αναρωτήθηκε στη
συνέχεια εάν υπάρχουν τριάδες φυσικών αριθμών που να ικανοποιούν τη σχέση α3
+ β3= γ3 ή ίσως
και την α4 + β4= γ4 δεν μπόρεσε να βρει ούτε μία τέτοια τριάδα
και κάπου εκεί ρωτώντας κάποιος φοιτητής του μαθηματικού του μίλησε για το
τελευταίο θεώρημα του Fermat.
Εξυπακούεται ότι κατά την εποχή της «εφηβικής του Αρχαιότητας» το
κομπιουτεράκι ως καθημερινή πρακτική δεν είχε κάνει την εμφάνισή του ούτε το
θεώρημα του Fermat
είχε αποδειχθεί από τον Andrew Wiles .
οι φιμπονάτσι
Η ακολουθία Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, 34,
55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657,
46368, 75025 . . Καθένας από τους όρους της προκύπτει από το άθροισμα των δύο
που προηγούνται. αν = αν-1
+ αν-2 .
Ο Leonardo
από την Πίζα - Leonardo Pisano, αποκαλούμενος Fibonacci,
γιος του Bonacci, - ο
μεγαλύτερος ίσως ευρωπαίος μαθηματικός του Μεσαίωνα, είχε καταλήξει σε αυτή την
ακολουθία παρακολουθώντας τις συνήθειες των κουνελιών όταν ζευγαρώνουν. Οι
«αριθμοί Fibonacci» εμφανίζονται στη φύση σε ένα
σωρό επεισόδια. Πόσα είναι τα πέταλα των λουλουδιών; Αν τα μετρήσουμε θα
καταλήξουμε σε αριθμό Fibonacci. Σε κάθε κουκουνάρι υπάρχουν έλικες. Πόσες είναι
οι έλικες σε ένα τυχαίο κουκουνάρι; Αν τις μετρήσουμε θα βρούμε κάποιον αριθμό Fibonacci.
Η ανάπτυξη των οστράκων
μέσα
στον χρόνο βρίσκεται επίσης σε αντιστοιχία με τους
αριθμούς
Fibonacci.
 Και το πιο παράξενο. Η
ακολουθία σχετίζεται με
Και το πιο παράξενο. Η
ακολουθία σχετίζεται με
το
κατασκεύασμα της ελληνίδας Γεωμετρίας που
λέγεται χρυσή τομή.
Κι
ακόμα: εάν προσθέσουμε διαγώνια τους
αριθμούς
στο τρίγωνο του
Pascal θα βρούμε τους φιμπονάτσι.
οι Βαβυλώνιοι
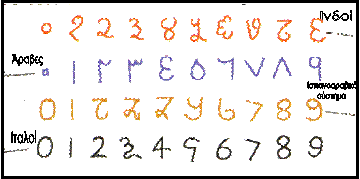
Συνέχεια ο φ, ο π, ο e, o
i, o μηδέν και
η συγκατοίκηση