![]()

1. Να
γνωρίζει την εξίσωση αρμονικού
κύματος.
Κατ’
αρχήν με τη μορφή Ψ=Αημω(t-x/c) ή Ψ= Αημ2π(tf-x/λ) αλλά και γενικότερα
Ψ=
Ασυν2π(x/λ
-ft) +iΑημ2π(x/λ- ft)
(μιγαδική
συνάρτηση η οποία συγκροτείται από ένα πραγματικό και ένα φανταστικό τμήμα)
ή την αλγεβρικά ισοδύναμη εκθετική μορφή Ψ=Αe2πi(x/λ -ft)
2. Να έχει κατανοήσει ότι
a.
εφόσον το σωματίδιο (λόγου χάριν, το ηλεκτρόνιο) είναι σωματίδιο-κύμα μπορούμε
να αντικαταστήσουμε το μήκος κύματος λ
με h/p, -p, η ορμή του σωματιδίου και h η σταθερά του Planck – σύμφωνα με την εξίσωση του De Broglie.
β.
εφόσον η ενέργεια θεωρείται κβαντισμένη, μπορούμε να
αντικαταστήσουμε τη συχνότητα f
με Ε/h,
σύμφωνα με την εξίσωση του Planck Ε= hf.
3.
Να γνωρίζει ότι η ορμή ενός σωματιδίου η κινητική του
ενέργεια και η μάζα του σχετίζονται με την p2=E/2m.
4.
Να γνωρίζει την έννοια ‘’παράγωγος’’ και
να είναι σε θέση να παραγωγίζει την απλή εκθετική
συνάρτηση Ψ = Αe f(x) , να γνωρίζει δηλαδή ότι η παράγωγος Ψ΄ είναι ίση με Αe
f(x) . f(x )΄.
Να μπορεί να προσδιορίζει ότι
η ως προς τον χρόνο t παράγωγος της
2πi(px-Et)/h είναι ίση με -Ε.
2πi/h
Να
μπορεί να προσδιορίζει ότι η ως προς x
παράγωγος της 2πi(px-Et)/h είναι
ίση με
p.2πi/h.
5. Να έχει κατανοήσει τη φυσική σημασία της μαθηματικής συνάρτησης
![]() (παραγώγου) η
οποία,
(παραγώγου) η
οποία,
ΑΝΑΦΕΡΕΤΑΙ σε ένα σημείο-θέση x- και στο σύνολο των χρονικών στιγμών
και
ΠΕΡΙΓΡΑΦΕΙ χρονική εξέλιξη της
τιμής της Ψ, ή, με άλλα λόγια,
τον ρυθμό
μεταβολής της Ψ ενός σημείου
6.
Να έχει κατανοήσει τη φυσική σημασία της
μαθηματικής συνάρτησης
![]() (παραγώγου) η οποία,
(παραγώγου) η οποία,
ΑΝΑΦΕΡΕΤΑΙ
σε συγκεκριμένη χρονική στιγμή και στο σύνολο των σημείων
και
ΠΕΡΙΓΡΑΦΕΙ
τη χωρική εξέλιξη της τιμής της Ψ, το
« πώς , δηλαδή, μεταβάλλεται η τιμή της Ψ κάθε σημείου συναρτήσει της θέσης του
σημείου».
7. Να έχει κατανοήσει
τη φυσική σημασία της μαθηματικής συνάρτησης
![]() (δεύτερης
παραγώγου) η οποία,
(δεύτερης
παραγώγου) η οποία,
ΑΝΑΦΕΡΕΤΑΙ
σε συγκεκριμένη χρονική στιγμή και στο σύνολο των σημείων
και
ΠΕΡΙΓΡΑΦΕΙ τη χωρική εξέλιξη της τιμής της ![]()
το «πώς, δηλαδή, μεταβάλλεται η τιμή της![]() κάθε
«γεωμετρικού» σημείου συναρτήσει της θέσης του σημείου».
κάθε
«γεωμετρικού» σημείου συναρτήσει της θέσης του σημείου».
![]()
![]()
[
1.
Στην ΑΦΕΤΗΡΙΑ μία ΕΞΙΣΩΣΗ της ΚΛΑΣΙΚΗΣ ΦΥΣΙΚΗΣ
η εξίσωση αρμονικού κύματος
Ψ
= Ασυν2π(x/λ -ft) +iΑημ2π(x/λ- f t) η οποία «κυκλοφορεί» και με τη μορφή
Ψ=Αe2πi(x/λ –f t) ώστε να διευκολύνεται η παραγώγιση.
2.
ΤΟ ΠΡΩΤΟ ΒΗΜΑ γίνεται με το
να «μπολιάσουμε» την εξίσωση αυτή της ΚΛΑΣΙΚΗΣ ΦΥΣΙΚΗΣ Φυσικής
με δύο γνωστικά στοιχεία της νεογέννητης τότε (έτος 1926) ΚΒΑΝΤΙΚΗΣ
ΦΥΣΙΚΗΣ.
Το ένα από τα στοιχεία είναι η ηλικίας , τότε, 26 ετών, εξίσωση
του Planck Ε= hf για την ενέργεια ενός κβάντου
ακτινοβολίας συχνότητας f .
Αντικαθιστούμε
το f
(συχνότητα) με
το ίσο του E/h βάση της εξίσωσης
Το δεύτερο στοιχείο είναι η ηλικίας, τότε, 3 ετών, εξίσωση του De Broglie για το σωματίδιο-κύμα. Είναι η λ=p/h η
οποία συσχετίζει το μέγεθος ΜΗΚΟΣ ΚΥΜΑΤΟΣ, τον βασικό εκφραστή της
κυματικότητας, με το μέγεθος ΟΡΜΗ που είναι ένας από τους βασικούς εκφραστές
της σωματιδιακότητας .
Αντικαθιστούμε
λοιπόν, και το λ (μήκος
κύματος) με το ίσο του p/h , οπότε έχουμε μπροστά μας την:
Ψ=Αe2πi(px-Et)/h
Βρισκόμαστε
μπροστά σε μία σχέση ένα από τα πρώτα δημιουργήματα του γάμου της Κλασικής
Φυσικής με την Κβαντική Φυσικής. Ας το δούμε με το βλέμμα ενός μαθηματικού
χωρίς να ξεχνάμε τη Φυσική και τη Χημεία.
Μπορούμε
να το δούμε ως μία ΣΥΝΑΡΤΗΣΗ (Ψ=Ψ(x,t) Ψ=Αe2πi(px-Et)/h)
η οποία μας «προσφέρει» τις τιμές της Ψ
ενός σωματιδίου, ενέργειας
Ε και ορμής p, αρκεί
εμείς, μέσα από τις τιμές των t και x να προτείνουμε το «που» και το «πότε».
Μπορούμε ωστόσο να το δούμε και με άλλους τρόπους.
3.
ΤΟ ΕΠΟΜΕΝΟ ΒΗΜΑ γίνεται με το να «δούμε» το, τότε,
«νεογέννητο» ως μία συνάρτηση της Ψ
με μοναδική μεταβλητή το t.
Ψ=Αe2πi(px-Et)/h
Σε
γλώσσα Φυσικής επιχειρούμε να «αντικρίσουμε» τις τιμές της Ψ ΣΕ ΕΝΑ ΣΗΜΕΙΟ ΤΟΥ
ΧΩΡΟΥ και στη συνέχεια να προσδιορίσουμε τη χρονική τους εξέλιξη, να
προσδιορίσουμε , με άλλα λόγια, τον ρυθμό της μεταβολής των τιμών της Ψ στο
συγκεκριμένο ΓΕΩΜΕΤΡΙΚΟ ΣΗΜΕΙΟ σημείο του χώρου.
Το
εγχείρημα αυτό, στη γλώσσα των μαθηματικών, λέγεται:
Προσδιορίζουμε τη (μερική) παράγωγο της Ψ ως προς τον χρόνο t
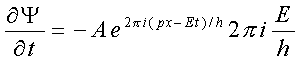
άρα i![]() = - 2πi2E/
h
.Ψ Αντικαθιστούμε το h/2π με το σύμβολο ћ
= - 2πi2E/
h
.Ψ Αντικαθιστούμε το h/2π με το σύμβολο ћ
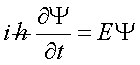 (1)
(1)
( Μας
λέει ότι σε
δεδομένο ΓΕΩΜΕΤΡΙΚΟ ΣΗΜΕΙΟ του χώρου ο
χρονικός ρυθμός μεταβολής της Ψ είναι ανάλογος με την τιμή της Ψ. Μας λέει
ακόμα ότι στη διαμόρφωση της αναλογίας συμμετέχει η τιμή της ενέργεια του
σωματιδίου )
4. ΕΝΑ ΑΚΟΜΗ ΒΗΜΑ
γίνεται με το να «δούμε το δημιούργημα» ως
μία
συνάρτηση της Ψ με μοναδική μεταβλητή
το x.
Ψ=Αe2πi(px-Et)/h
Σε
γλώσσα Φυσικής επιχειρούμε να «αντικρίσουμε» τις τιμές της Ψ ΣΕ ΜΙΑ ΧΡΟΝΙΚΗ
ΣΤΙΓΜΗ και στο σύνολο των ΓΕΩΜΕΤΡΙΚΩΝ
ΣΗΜΕΙΩΝ του ΧΩΡΟΥ και στη συνέχεια να
προσδιορίσουμε τη χωρική τους εξέλιξη ,
να προσδιορίσουμε , με άλλα λόγια, « πώς
μεταβάλλεται η τιμή της Ψ κάθε
ΓΕΩΜΕΤΡΙΚΟΥ ΣΗΜΕΙΟΥ συναρτήσει της
θέσης, x, του ΓΕΩΜΕΤΡΙΚΟΥ αυτού ΣΗΜΕΙΟΥ .
Το εγχείρημα αυτό, στη
γλώσσα των μαθηματικών, λέγεται:
Προσδιορίζουμε τη (μερική) παράγωγο της Ψ ως προς τη θέση x
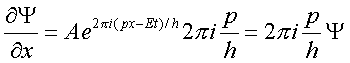
( Μας λέει ότι σε δεδομένη χρονική στιγμή η χωρική εξέλιξη της Ψ , η ∂Ψ/∂x είναι ανάλογη με την τιμή της Ψ. Μας λέει ακόμα ότι στη διαμόρφωση της αναλογίας συμμετέχει η τιμή της ορμής του σωματιδίου )
5. ΤΟ
ΤΕΛΙΚΟ ΒΗΜΑ είναι να «δούμε» τη συνάρτηση ∂Ψ/∂x που προέκυψε ως συνάρτηση με μοναδική
μεταβλητή το x.
Να παγώσουμε δηλαδή και πάλι τον χρόνο (αναφερόμενοι σε ΜΙΑ
στιγμή του ΧΡΟΝΟΥ) και να ερευνήσουμε την εξέλιξη
των τιμών της, το « πώς»
δηλαδή μεταβάλλεται η τιμή της ∂Ψ/∂x κάθε
ΓΕΩΜΕΤΡΙΚΟΥ ΣΗΜΕΙΟΥ συναρτήσει της
θέσης, x, του ΓΕΩΜΕΤΡΙΚΟΥ αυτού ΣΗΜΕΙΟΥ .
Το εγχείρημα αυτό, στη
γλώσσα των μαθηματικών, λέγεται:
Προσδιορίζουμε
τη (μερική)
παράγωγο της παραπάνω συνάρτησης ως προς τη
θέση x .
Είναι η λεγόμενη δεύτερη παράγωγος της Ψ, ως προςx.
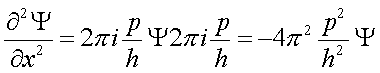
και εφόσον p2=2mE (m, η μάζα και Ε, η ενέργεια) και i2= -1
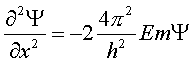 Αντικαθιστούμε
το h/2π
με το σύμβολο ћ
Αντικαθιστούμε
το h/2π
με το σύμβολο ћ
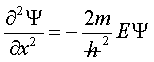 άρα
άρα
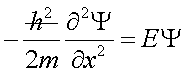 (2)
(2)
( Μας λέει ότι σε δεδομένη χρονική στιγμή η χωρική εξέλιξη της ∂Ψ/∂x, η ∂2Ψ/∂x2, είναι
ανάλογη με την τιμή της Ψ. Μας λέει ακόμα ότι στη διαμόρφωση της αναλογίας
συμμετέχει η τιμή της μάζας του
σωματιδίου )
Από τα παραπάνω προκύπτει
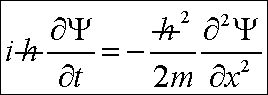 (3)
(3)
Μας
λέει ότι σε δεδομένη χρονική στιγμή η
χρονική μεταβολή της Ψ είναι ανάλογη με
τη «χωρική εξέλιξη των τιμών της χωρικής εξέλιξης της Ψ». Βέβαια προκειμένου για τη φράση «η χωρική
εξέλιξη των τιμών της χωρικής εξέλιξης της Ψ». η γλώσσα των συμβόλων (∂2Ψ/∂x2
) είναι
προτιμότερη. Μας λέει ακόμα ότι στη
διαμόρφωση της αναλογίας συμμετέχει η τιμή της μάζας του σωματιδίου )
![]()
Εδώ η προσπάθεια να περιγράψουμε την
Κυματοσυνάρτηση Ψ έχει ήδη οδηγηθεί
στη συγκομιδή κάποιων «παράξενων»
πληροφοριών σχετικά με το «πώς», η
Ψ, «υπάρχει» μέσα στον ΧΩΡΟ και στον
ΧΡΟΝΟ. Η Εξίσωση, όμως, στην οποία καταλήξαμε έγινε πολύτιμη για την εξέλιξη
της νεογέννητης Κβαντομηχανικής μόνο μετά τον εμπλουτισμό της.
Κι αυτό γιατί μέχρι τώρα το μοντέλο μας είχε δύο
σοβαρούς περιορισμούς. Ο πρώτος ήταν ότι αναφερόταν σε ΜΙΑ ΔΙΑΣΤΑΣΗ και ο
δεύτερος ότι ΑΓΝΟΟΥΣΕ ΤΙΣ ΑΛΛΗΛΕΠΙΔΡΑΣΕΙΣ του σωματιδίου με το υπόλοιπο Σύμπαν.
Στα παρακάτω θα επιχειρήσουμε να εμπλουτίσουμε την σχέση
στην οποία έχουμε οδηγηθεί, παίρνοντας υπόψη
και το τρισδιάστατο του ευκλείδειου χώρου και την ύπαρξη των
αλληλεπιδράσεων.
![]()
![]()
![]()
Τα
παραπάνω είχαν στην αφετηρία την εξίσωση ενός «μοντέλου» κύματος διαδιδόμενου
κατά τη μία διάσταση. Αναφέρονται συνεπώς σε μία ΜΙΑ ΔΙΑΣΤΑΣΗ. Στη γενικότερη
περίπτωση των τριών διαστάσεων η εξίσωση παίρνει τη μορφή
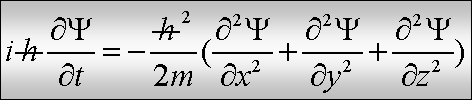 (4)
(4)
Μπορούμε,
χρησιμοποιώντας τον λαπλασιανό τελεστή Ñ2, να έχουμε την «απλούστερη» μορφή
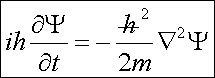 (4α)
(4α)
![]()
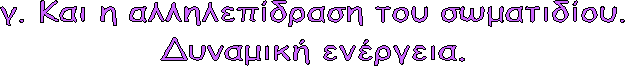
Τα
παραπάνω υποδήλωναν ότι το σωματίδιο κινείται χωρίς να αλληλεπιδρά και η
αναφερόμενη «ενέργεια» υποδήλωνε την κινητική ενέργεια.
Στη
γενικότερη περίπτωση που το σωματίδιο ΑΛΛΗΛΕΠΙΔΡΑ χρειάζεται
να
θυμηθούμε και την περιγράφουσα την αλληλεπίδραση ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ και
να
προσθέσουμε μία συνάρτηση θέσης V(x)
Επιστρέφουμε
στην εξίσωση (2) 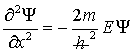 -την
αναφερόμενη βέβαια σε μία διάσταση-
στην οποία «συμμετέχει» η ενέργεια και την παρουσιάζουμε με τη μορφή
-την
αναφερόμενη βέβαια σε μία διάσταση-
στην οποία «συμμετέχει» η ενέργεια και την παρουσιάζουμε με τη μορφή
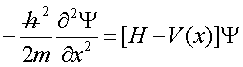 (5)
(5)
στην
οποία το σύμβολο Η εκφράζει την ολική ενέργεια.
Η
αντίστοιχη σε τρεις διαστάσεις και με τη χρήση του λαπλασιανού τελεστή είναι η
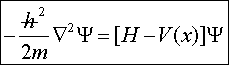 (5α)
(5α)
Μπορούμε
επίσης να επιστρέψουμε στην -αναφερόμενη σε τρεις διαστάσεις εξίσωση- (4α) και να την παρουσιάσουμε με τη μορφή
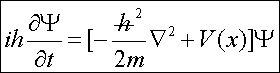 (6)
(6)
![]()
![]()
Ας δούμε τώρα τις έξη εξισώσεις. Οι 1, 2, 3 και 5 αναφέρονται σε
μία διάσταση
![]()
Στην εξίσωση (1) 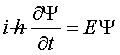 συμμετέχουν
συμμετέχουν
ο ρυθμός
μεταβολής της Ψ,
η Ψ
και η ενέργεια του σωματιδίου.
Η εξίσωση δεν περιγράφει
αλληλεπίδραση του σωματιδίου
![]()
Στην εξίσωση (2) ![]() συμμετέχουν
συμμετέχουν
η δεύτερη παράγωγος της Ψ ως προς x
η Ψ
και η ενέργεια του σωματιδίου
Η εξίσωση δεν περιγράφει αλληλεπίδραση του σωματιδίου
![]()
Στην εξίσωση (3) 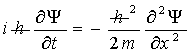 συμμετέχουν
συμμετέχουν
ο ρυθμός
μεταβολής της Ψ,
η δεύτερη παράγωγος της Ψ ως προς x
και η
μάζα του σωματιδίου
Η εξίσωση δεν περιγράφει
αλληλεπίδραση του σωματιδίου
![]()
H εξίσωση (4), γενίκευση της (3) ως αναφερόμενη σε
τρεις διαστάσεις, είναι η συνήθως εμφανιζόμενη ως εξίσωση Schrödinger, χωρίς αλληλεπίδραση του
σωματιδίου.

Σ’ αυτήν συμμετέχουν οι ίδιες έννοιες εκείνες της προηγούμενης
(3).
H εξίσωση (4α) είναι η (4) με άλλο συμβολισμό
![]()
H εξίσωση (5)
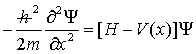
αναφέρεται σε μία διάσταση
ενώ
περιγράφει και την αλληλεπίδραση
![]()
H εξίσωση (6) 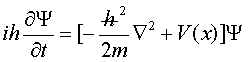
αναφέρεται σε τρεις διαστάσεις
ενώ
περιγράφει και την αλληλεπίδραση.
Σ’
αυτήν συμμετέχουν
η Ψ,
ο ρυθμός
μεταβολής της Ψ,
η δυναμική
ενέργεια του σωματιδίου ως συνάρτηση θέσης
και
η Ñ2 Ψ, το άθροισμα δηλαδή της δεύτερης παραγώγου της Ψ ως προς x, με τις αντίστοιχες ως προς y και z .
![]()
![]()
![]() Επιστροφή στην κεντρική σελίδα
Επιστροφή στην κεντρική σελίδα