Ανδρέας Ιωάννου Κασσέτας

Τρία ερωτήματα σε ζητήματα Μηχανικής

1. Σε ένα αρχικά ακίνητο σώμα ασκούνται δυνάμεις η σύνθεση των οποίων

καταλήγει σε ένα ζεύγος δυνάμεων . Το σώμα

Θα εκτελέσει στροφική κίνηση περί άξονα κάθετο στο επίπεδο του ζεύγους ο οποίος διέρχεται από το ΚΕΝΤΡΟ ΜΑΖΑΣ

Θα εκτελέσει στροφική κίνηση περί άξονα κάθετο στο επίπεδο του ζεύγους ο οποίος ΔΕΝ διέρχεται από το ΚΕΝΤΡΟ ΜΑΖΑΣ

Θα εκτελέσει σύνθετη κίνηση αναλυόμενη σε στροφική περί το κέντρο μάζας και μεταφορική

Με ποιο από τα παραπάνω συμφωνείτε;

2. Σε μία ομογενή κατακόρυφο ράβδο αναρτημένη από το ανώτερο σημείο της Ο

και αρχικώς ακίνητη ασκείται οριζόντια δύναμη F στο κατώτερο σημείο της Α

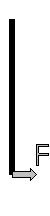1. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται σε ζεύγος

2. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται σε μία οριζόντια δύναμη F

διερχόμενη από το κέντρο μάζας και σε ένα ζεύγος δυνάμεων

3. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται στην ασκούμενη

στο σημείο Α δύναμη F και σε ζεύγος δυνάμεων

4. Η ασκούμενη στη ράβδο δύναμη στο σημείο Ο είναι κατακόρυφη

5. Η ασκούμενη στη ράβδο δύναμη στο σημείο Ο έχει οριζόντια συνιστώσα

με κατεύθυνση αντίθετη της F

6. Η επιτάχυνση του κέντρου μάζας θα είναι ίση με F/m όπου m η μάζα της ράβδου

7. Η επιτάχυνση του κέντρου μάζας θα έχει συνιστώσα προς το σημείο ανάρτησης Ο

Με ποια από τα παραπάνω συμφωνείτε;

Η ροπή αδράνειας της ράβδου ως προς άξονα κάθετο σε αυτήν - διερχόμενο από το κέντρο μάζας - είναι ίση με mL²/12

3. Μια μπίλια σε κεκλιμένο επίπεδο. Αφήνεται από ένα σημείο και κυλάει προς τα κάτω.

Η κίνησή της μπορεί να αναλυθεί σε μεταφορική με την ταχύτητα του κέντρου μάζας

και σε στροφική περί άξονα που περνάει από το κέντρο μάζας.

Εφαρμόζουμε το θεώρημα έργου ενέργειας για τη μεταφορική κίνηση και για μετατόπιση x ,

οπότε ½mυ_cm² = mgxημφ – Τx .

Το ερώτημα βέβαια είναι « η αρνητική ποσότητα –Τx είναι το έργο της στατικής τριβής ; »

Αλλά η στατική τριβή εκτελεί έργο ; »

Και στη συνέχεια για τη στροφική κίνηση Τx = ½ I_cmω².

Το ερώτημα βέβαια είναι « η θετική ποσότητα Τx είναι το έργο της στατικής τριβής ; »

Το αποτέλεσμα στο οποίο καταλήγουμε ½mυ_cm² + ½ I_cmω²= mgxημφ εναρμονίζεται με τη Διατήρηση της Ενέργειας.

Τι συμβαίνει τελικά;

Μπορούμε να εφαρμόζουμε το θεώρημα έργου ενέργειας για κάθε μια κίνηση

( μεταφορική και στροφική ) χωριστά ;

Μήπως υπό προϋποθέσεις μπορούμε να δεχθούμε ότι η στατική τριβή εκτελεί έργο;

Η απάντηση στο τρίτο ερώτημα