ΘΕΜΑ 1ο

Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1 - 4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.

1. Αν η εξίσωση ενός αρμονικού κύματος είναι y = 10ημ(6πt - 2πx) στο S.I., τότε η ταχύτητα διάδοσης του κύματος είναι ίση με:

α. 10m/s β. 6m/s γ. 2m/s δ. 3m/s. Μονάδες 5

2. Δύο όμοιες πηγές κυμάτων Α και Β στην επιφάνεια μιας ήρεμης λίμνης βρίσκονται σε φάση και παράγουν υδάτινα αρμονικά κύματα. Η καθεμιά παράγει κύμα (πρακτικά) αμείωτου πλάτους 10cm και μήκους κύματος 2m. Ένα σημείο Γ στην επιφάνεια της λίμνης απέχει από την πηγή Α απόσταση 6m και από την πηγή Β απόσταση 2m. Το πλάτος της ταλάντωσης του σημείου Γ είναι :

α. 0cm β. 10cm γ. 20cm δ. 40cm . Μονάδες 5

3. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο μέσων. Όταν η διαθλώμενη ακτίνα κινείται παράλληλα προς τη διαχωριστική επιφάνεια, τότε η γωνία πρόσπτωσης ονομάζεται :

α. μέγιστη γωνία β. ελάχιστη γωνία

γ. μηδενική γωνία δ. κρίσιμη γωνία. Μονάδες 5

ΕΙΝΑΙ ΔΥΝΑΤΟΝ ΝΑ ΣΥΜΒΕΙ ;

Αν σεβαστούμε την αυστηρή γλώσσα της γεωμετρίας, το περιγραφόμενο ΔΕΝ ΜΠΟΡΕΙ ΝΑ ΣΥΜΒΕΙ.

ΜΙΑ ΦΩΤΕΙΝΗ ΑΚΤΙΝΑ ΔΙΑΔΙΔΟΜΕΝΗ ΠΑΡΑΛΛΗΛΑ ΠΡΟΣ ΤΗ ΔΙΑΧΩΡΙΣΤΙΚΗ ΕΠΙΦΑΝΕΙΑ ΔΕΝ ΔΙΑΘΛΑΤΑΙ ΔΙΟΤΙ ΔΕΝ ΛΑΜΒΑΝΕΙ ΧΩΡΑ «ΠΡΟΣΠΤΩΣΗ» και σύμφωνα με την Αρχή της αντίστροφης πορείας δεν μπορεί μία διαθλώμενη ακτίνα να είναι παράλληλη προς τη διαχωριστική επιφάνεια.

Το ζήτημα είναι αρκετά λεπτό δεδομένου ότι υπεισέρχεται η έννοια της οριακής συνθήκης.

Η ΝΙΚΗ ΤΗΣ ΑΜΕΡΙΚΑΝΙΚΗΣ «ΚΡΙΣΙΜΗΣ ΓΩΝΙΑΣ» πάνω στην ΕΥΡΩΠΑΪΚΗ «ΟΡΙΚΗ ΓΩΝΙΑ»

Εξάλλου σε όλες σχεδόν τις ευρωπαϊκές γλώσσες (γαλλική, ισπανική , ιταλική, γερμανική και όχι μόνο) η συγκεκριμένη γωνία χαρακτηρίζεται ΟΡΙΚΗ ΓΩΝΙΑ. Οι Ιταλοί τη λένε angolo limite και οι Γερμανοί Grenzwinkel

το οποίο αποδίδεται ως ορική γωνία. Είναι βέβαια οι Αμερικανοί που την χαρακτηρίζουν critical angle - κρίσιμη γωνία. Εδώ και πολλές δεκαετίες στην ελληνική εκπαίδευση είχε εδραιωθεί η «ευρωπαϊκή» επιλογή ΟΡΙΚΗ ΓΩΝΙΑ η οποία κατά την άποψή μας συμβάλλει πιο αποτελεσματικά στο να κατανοηθεί η οριακή συνθήκη.

Γιατί άραγε η επιλογή αυτή εγκαταλείφθηκε και προτιμήθηκε η αμερικάνικη επιλογή; Βέβαια οι μόνοι που δεν ευθύνονται είναι οι συγγραφείς των σχολικών εγχειριδίων και οι μόνοι που ευθύνονται είναι οι συντάκτες των αντίστοιχων Προγραμμάτων Σπουδών οι οποίοι επέβαλαν τον όρο ΚΡΙΣΙΜΗ ΓΩΝΙΑ και τον αντίστοιχο «διδακτικά άθλιο» συμβολισμό θ_crit , υποχρεώνοντες τους συγγραφείς να ακολουθούν τον συμβολισμό του USA βιβλίου του YOUNG. Γιατί άραγε;

4. Ο ωροδείκτης ενός ρολογιού έχει περίοδο σε ώρες (h):

α. 1h β. 12h γ. 24h δ. 48h Μονάδες 5

ΜΙΑ ΣΚΕΨΗ

Τι ακριβώς επιδιώκουμε να αξιολογήσουμε με το ερώτημα 4 ; Παρόμοια ερώτημα θα μπορούσε να τεθεί σε μαθητές Γ΄ Γυμνασίου και να θεωρηθεί, από τους περισσότερους, ιδιαίτερα απλό.

5. Να γράψετε στο τετράδιό σας το γράμμα της πρότασης και δίπλα τη λέξη που τη συμπληρώνει σωστά.

α. Στη σύνθεση δύο αρμονικών ταλαντώσεων της ίδιας διεύθυνσης, που γίνονται γύρω από το ίδιο σημείο με το ίδιο πλάτος και λίγο διαφορετικές συχνότητες, ο χρόνος ανάμεσα σε δύο διαδοχικές μεγιστοποιήσεις του πλάτους ονομάζεται . . . . . . του διακροτήματος. ΠΕΡΙΟΔΟΣ

β. Η ταυτόχρονη διάδοση δύο ή περισσοτέρων κυμάτων στην ίδια περιοχή ενός ελαστικού μέσου ονομάζεται . . . . . . .

( Επιδιωκόμενη απάντηση είναι . . . . ΣΥΜΒΟΛΗ)

ΜΙΑ ΠΑΡΑΤΗΡΗΣΗ.

Η συμβολή είναι φαινόμενο που θα λάβει χώρα εφόσον δύο ή περισσότερα κύματα συμβεί να διαδίδονται ταυτόχρονα στη ίδιο χώρο. Με άλλα λόγια ΣΥΜΒΟΛΗ ΔΕΝ ΕΙΝΑΙ Η ΔΙΑΔΟΣΗ. Είναι «αυτό που θα γίνει » εφόσον συμβαίνει ταυτόχρονη διάδοση.

Ωστόσο εικάζουμε ότι δεν θα δημιουργηθεί πρόβλημα και οι μαθητές που θα έχουν γνώση του ζητήματος θα συμπληρώσουν με τη λέξη ΣΥΜΒΟΛΗ

γ. Όταν ένα σώμα μετακινείται στο χώρο και ταυτόχρονα αλλάζει ο προσανατολισμός του, λέμε ότι κάνει . . . . . . . κίνηση.

ΜΙΑ ΠΑΡΑΤΗΡΗΣΗ.

Η έννοια «προσανατολισμός ενός σώματος» έχει σοβαρά προβλήματα εννοιακής οικοδόμησης. Κάτι ανάλογο, αλλά σε μικρότερο βαθμό, ισχύει και για το σημαινόμενο της φράσης «ένα σώμα μετακινείται» η οποία διατυπώνεται έτσι ώστε να μη θεωρείται ισοδύναμη με τη φράση «ένα σώμα κινείται» .

Τι συμβαίνει, λόγου χάριν, με την αρχικά οριζόντια ράβδο του ΘΕΜΑΤΟΣ 4 η οποία, μετά το κόψιμο του νήματος, στρέφεται διατηρούμενη σε κατακόρυφο επίπεδο. ΜΕΤΑΚΙΝΕΙΤΑΙ ή δεν ΜΕΤΑΚΙΝΕΙΤΑΙ; Και τι συμβαίνει με τον προσανατολισμό της; ΑΛΛΑΖΕΙ ή δεν ΑΛΛΑΖΕΙ; Επειδή κατά μία έννοια και ΜΕΤΑΚΙΝΕΙΤΑΙ και ΑΛΛΑΖΕΙ Ο ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΤΗΣ θα ήταν νόμιμο να απαντήσουμε ότι για τη ΣΤΡΟΦΙΚΗ αυτή ΚΙΝΗΣΗ ισχύει η παραπάνω περιγραφή (του ζητήματος γ.) να απαντήσουμε ότι «ένα σώμα που μετακινείται στο χώρο και αλλάζει ο προσανατολισμός του κάνει ΣΤΡΟΦΙΚΗ κίνηση» και να μηδενιστούμε από τον βαθμολογητή.

Βέβαια όσοι μαθητές χρησιμοποίησαν τη μνήμη τους και ανέτρεξαν στη σχετική (κατά την άποψή μας προβληματική) φράση του σχολικού εγχειριδίου συμπλήρωσαν με τη λέξη ΣΥΝΘΕΤΗ και απέφυγαν τον μηδενισμό.

Εικάζουμε ότι μετά τις διορθώσεις θα καταδειχθεί ότι το συγκεκριμένο θέμα θα παρουσιάσει πρόβλημα.

δ. Ένας παρατηρητής ακούει ήχο με συχνότητα . . . . . . . από τη συχνότητα μιας πηγής, όταν η μεταξύ τους απόσταση ελαττώνεται. ΜΕΓΑΛΥΤΕΡΗ

ε. Τα σημεία που πάλλονται με μέγιστο πλάτος ταλάντωσης σε ένα στάσιμο κύμα ονομάζονται . . . . . . ΚΟΙΛΙΕΣ Μονάδες 5

ΘΕΜΑ 2ο

1. Σε αρμονικό ηλεκτρομαγνητικό κύμα που διαδίδεται στο κενό το ηλεκτρικό πεδίο περιγράφεται στο S.I από την εξίσωση Ε=30ημ2π(6×10¹⁰t - 2×10²x). Να εξετάσετε αν το μαγνητικό πεδίο του παραπάνω ηλεκτρομαγνητικού κύματος περιγράφεται στο S.I από την εξίσωση Β=10^-7ημ2π(6×10¹⁰t - 2×10²x).

Δίνεται: ταχύτητα του φωτός στο κενό c₀= 3×10⁸ m/s. Μονάδες 6

2. Καλλιτέχνης του πατινάζ περιστρέφεται γύρω από τον άξονά του, χωρίς τριβές. Στην αρχή ο καλλιτέχνης έχει τα χέρια απλωμένα και στη συνέχεια τα συμπτύσσει. Ο καλλιτέχνης περιστρέφεται πιο γρήγορα, όταν έχει τα χέρια:

α. απλωμένα β. συνεπτυγμένα. Μονάδες 2

Να δικαιολογήσετε την απάντησή σας. Μονάδες 4

Ο ΚΟΣΜΟΣ ΤΟΥ ΣΥΓΚΕΚΡΙΜΕΝΟΥ ΚΑΙ Η ΠΕΡΙΟΧΗ ΤΗΣ ΑΦΑΙΡΕΣΗΣ

Πρόκειται για ένα αρκετά δύσκολο ζήτημα όπου με βάση μία περιγραφή ενός φαινομένου ζητείται μία ερμηνεία η οποία απαιτεί μία πληθώρα εννοιών.

Από τη μία λοιπόν η περιγραφή του φαινομένου. Χρησιμοποιεί στοιχεία κυρίως από τον κόσμο του ΣΥΓΚΕΚΡΙΜΕΝΟΥ. Πατινάζ, άνθρωπος καλλιτέχνης μάλλον γένους αρσενικού, απλωμένα χέρια, σύμπτυξη των χεριών, περιστροφή, η έννοια πιο γρήγορα, τριβές. Ακόμα και το σημαινόμενο της φράσης ΧΩΡΙΣ ΤΡΙΒΕΣ παραπέμπει λιγότερο στην έννοια της φυσικής ( η τριβή ολίσθησης είναι μία δύναμη) και περισσότερο στο αντίστοιχο σημαινόμενο της καθημερινής εμπειρίας σύμφωνα με την οποία ΟΙ ΤΡΙΒΕΣ ΕΙΝΑΙ ΚΑΤΙ ΠΟΥ ΣΧΕΤΙΖΕΤΑΙ ΜΕ ΤΗΝ ΠΡΑΞΗ ΤΟΥ ΤΡΙΒΩ. Μοναδικό αφηρημένο στοιχείο είναι το γεωμετρικό στοιχείο «ΑΞΟΝΑΣ ΤΟΥ ΚΑΛΛΙΤΕΧΝΗ» λες και ο καλλιτέχνης ΕΧΕΙ ΑΞΟΝΑ. Θα μπορούσε να χρησιμοποιηθεί η διατύπωση «στρέφεται γύρω από κατακόρυφο άξονα».

Στην «άλλη όχθη» η ζητούμενη ερμηνεία. Απαιτεί ΦΥΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΝΟΜΟΥΣ που ανήκουν στη σφαίρα της ΑΦΑΙΡΕΣΗΣ. Ασκούμενες εξωτερικές δυνάμεις, ροπές εξωτερικών δυνάμεων κατά τη διεύθυνση κάποιου άξονα, γωνιακή ταχύτητα, ροπή αδράνειας ως προς κάποιον άξονα, στροφορμή κατά τη διεύθυνση κάποιου άξονα, αρχή της διατήρησης της στροφορμής, σχέση στροφορμής στρεφομένου σώματος με τη ροπή αδράνειας και τη γωνιακή ταχύτητα.

Προβλέπουμε ότι ενώ θα είναι πάρα πολλοί οι μαθητές και οι μαθήτριες που θα δώσουν τη σωστή απάντηση βασιζόμενοι και βασιζόμενες σε εμπειρία μνήμη, η δικαιολόγηση της απάντησης θα δημιουργήσει μεγάλες δυσκολίες και η απόδοση των 4 μονάδων σε όσους καταφέρουν να δώσουν μια ολοκληρωμένη απάντηση είναι κατά την άποψή μας ιδιαίτερα πτωχή.

3. Σφαίρα A που κινείται σε λείο οριζόντιο επίπεδο συγκρούεται κεντρικά και πλαστικά με άλλη όμοια αλλά ακίνητη σφαίρα Β που βρίσκεται στο ίδιο επίπεδο. Να αποδείξετε ότι η κινητική ενέργεια του συσσωματώματος μετά την κρούση είναι ίση με το μισό της κινητικής ενέργειας της σφαίρας Α, πριν από την κρούση. Μονάδες 7

4. Σώμα μάζας m εκτελεί γραμμική απλή αρμονική ταλάντωση. Η απομάκρυνση x του σώματος από τη θέση ισορροπίας δίνεται από τη σχέση x=Αημωt, όπου Α το πλάτος της ταλάντωσης και ω η γωνιακή συχνότητα. Να αποδείξετε ότι η συνολική δύναμη, που δέχεται το σώμα σε τυχαία θέση της τροχιάς του, δίνεται από τη σχέση

F= - mω²x. Μονάδες 6

ΘΕΜΑ 3ο

Το ηλεκτρικό κύκλωμα του σχήματος αποτελείται από πυκνωτή με χωρητικότητα 2×10^-5 F , ένα ιδανικό πηνίο με συντελεστή αυτεπαγωγής 0,05H και διακόπτη Δ όπως φαίνονται στο παρακάτω σχήμα. Αρχικά ο διακόπτης Δ είναι ανοικτός και ο πυκνωτής είναι φορτισμένος με ηλεκτρικό φορτίο 5×10^-7 C. Οι αγωγοί σύνδεσης έχουν αμελητέα αντίσταση.

Τη χρονική στιγμή t=0 κλείνουμε το διακόπτη Δ.

Να υπολογίσετε:

1. την περίοδο της ηλεκτρικής ταλάντωσης Μονάδες 7

2. το πλάτος της έντασης του ρεύματος Μονάδες 8

3. την ένταση του ρεύματος τη στιγμή που το φορτίο του πυκνωτή C είναι 3×10^-7 C. Μονάδες 10 Δίνεται: π = 3,14 .

ΠΑΡΑΤΗΡΗΣΕΙΣ

1. Η διατύπωση του ΘΕΜΑΤΟΣ 3 έγινε χωρίς τη χρήση συμβόλων των μεγεθών. Δεν δόθηκε δηλαδή η διατύπωση «πυκνωτής χωρητικότητας C = 2×10^-5 F» αλλά «πυκνωτής χωρητικότητας 2×10^-5 F» και το ίδιο συνέβη με την τιμή του συντελεστή αυτεπαγωγής και με τις δύο τιμές του φορτίου.

Η παρουσίαση αυτή, μολονότι θα δυσκολέψει τους μαθητές που έχουν απομνημονεύσει «τύπους» και σύμβολα χωρίς να έχουν κατανοήσει τις αντίστοιχες έννοιες, ΚΡΙΝΕΤΑΙ ΙΔΙΑΙΤΕΡΑ ΘΕΤΙΚΗ και κατά την εκτίμησή μας πρέπει να δώσουμε ΣΥΓΧΑΡΗΤΗΡΙΑ στους συναδέλφους της Επιτροπής οι οποίοι μερίμνησαν γι αυτό.

2. Σχετικά με το ζητούμενο πλάτος της έντασης του ρεύματος ο μαθητής που θα γράψει τη σχέση

Ι = Qω = Q2π/Τ και στη συνέχεια θα αντικαταστήσει με τις τιμές θα βαθμολογηθεί με άριστα.

Και αυτό διότι ο «τύπος» Ι = Qω είναι ένας από τους 81 «τύπους» που απαιτείται να έχουν απομνημονεύσει οι μαθητές στο συγκεκριμένο μάθημα.

Ως πότε θα συνεχίζεται αυτή η πρακτική με τους δεκάδες απομνημονεύσιμους τύπους;

ΑΝΗΚΕΙ ΣΤΟΥΣ ΣΤΟΧΟΥΣ ΤΗΣ ΔΙΔΑΣΚΑΛΙΑΣ ΤΗΣ ΦΥΣΙΚΗΣ ΤΟ ΝΑ ΞΕΡΟΥΝ ΟΙ ΜΑΘΗΤΕΣ ΤΟΝ «ΤΥΠΟ» Ι = Qω;

Κατά τη γνώμη μας η σχέση Ι = Qω δεν έπρεπε να ανήκει στις απομνημονεύσιμες και οι μαθητές να ΑΞΙΟΛΟΓΗΘΟΎΝ όχι για το αν θυμούνται ένα δευτέρας κατηγορίας τύπο αλλά για το «εάν είναι σε θέση να εφαρμόσουν τον νόμο για τη Διατήρηση της ενέργειας» και κληθούν να την αποδείξουν τη σχέση βασιζόμενοι στη Διατήρηση της ενέργειας, όπως εξάλλου πιστεύουμε ότι θα ότι συμβεί με αρκετούς μαθητές οι καθηγητές των οποίων τους έπεισαν ότι το βασικό ζητούμενο δεν είναι να θυμούνται τύπους αλλά να βασίζονται στη γνώση των μεγάλων νόμων και να είναι σε θέση να τους εφαρμόζουν.

Υπό αυτή την έννοια θα είχε κάποια λογική το να βαθμολογούνται με 8 μονάδες το ζήτημα. Έτσι όμως όπως είναι τα πράγματα διαφωνούμε απόλυτα με τη απόδοση των 8 μονάδων στους μαθητές που ξέρουν ότι Ι = Qω.

ΘΕΜΑ 4ο

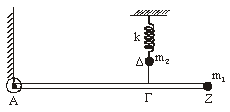
Ομογενής άκαμπτη ράβδος ΑΖ έχει μήκος L = 4m, μάζα M = 3kg και ισορροπεί σε οριζόντια θέση, όπως φαίνεται στο σχήμα. Στο άκρο της Α υπάρχει ακλόνητη άρθρωση γύρω από την οποία η ράβδος μπορεί να περιστρέφεται, χωρίς τριβές, ενώ στο άλλο άκρο της Ζ υπάρχει στερεωμένο σφαιρίδιο μάζας m₁ = 0,6kg και αμελητέων διαστάσεων. Ένα αβαρές τεντωμένο νήμα ΔΓ συνδέει το σημείο Γ της ράβδου με σφαιρίδιο μάζας m₂ = 1kg, το οποίο είναι στερεωμένο στο ελεύθερο άκρο ιδανικού ελατηρίου σταθεράς k = 100 N/m. Το άλλο άκρο του ελατηρίου είναι ακλόνητο. Η απόσταση ΑΓ είναι ίση με 2,8m. Όλη η διάταξη βρίσκεται στο ίδιο κατακόρυφο επίπεδο, στο οποίο γίνονται και όλες οι κινήσεις.

Α. Να υπολογίσετε:

Α.1 τη ροπή αδράνειας του συστήματος ράβδου – σφαιριδίου m₁ ως προς τον οριζόντιο άξονα που διέρχεται από το σημείο Α και είναι κάθετος στο επίπεδο της διάταξης Μονάδες 6

Α.2 το μέτρο της τάσης του νήματος ΔΓ. Μονάδες 6

Β. Αν κόψουμε το νήμα ΔΓ, το σφαιρίδιο m₂ εκτελεί αμείωτη αρμονική ταλάντωση, ενώ η ράβδος μαζί με το σώμα m₁, υπό την επίδραση της βαρύτητας, περιστρέφoνται χωρίς τριβές γύρω από το σημείο Α.

Να υπολογίσετε:

Β.1 το χρόνο που χρειάζεται το σφαιρίδιο m₂ από τη στιγμή που κόβεται το νήμα μέχρι τη στιγμή που θα φθάσει στην ψηλότερη θέση του για πρώτη φορά Μονάδες 6

Β.2 το μέτρο της γραμμικής ταχύτητας του σημείου Ζ, τη στιγμή που η ράβδος περνάει από την κατακόρυφη θέση. Μονάδες 7

Δίνονται: g = 10ms^-2, ροπή αδράνειας της ράβδου ως προς το κέντρο μάζας της: I_CM= 1/12 ML² , , π = 3,14.

ΠΑΡΑΤΗΡΗΣΕΙΣ

1. Επί τέλους. Μετά από δεκαπέντε περίπου χρόνια ταλαιπωρίας η μονάδα χιλιόγραμμο συμβολίζεται με τον σωστό τρόπο. kg και όχι Kg.

2. Θα μπορούσε να αποφευχθεί η διατύπωση ΤΟ ΜΕΤΡΟ ΤΗΣ ΤΑΣΗΣ ΤΟΥ ΝΗΜΑΤΟΣ. Και αυτό διότι και ο όρος δεν είναι για τους Φυσικούς έγκυρος ( για τους μηχανικούς σημαίνει άλλο πράγμα) και διότι όταν ζητάμε από τους μαθητές να προσδιορίσουν το στοιχείο μιας δύναμης, σύμφωνα με τη Διδακτική των Επιστημών, οφείλουμε να τους αποσαφηνίσουμε σε ποια ακριβώς δύναμη αναφερόμαστε. Τη δύναμη που ασκεί το νήμα στο ελατήριο; Τη δύναμη που ασκεί το ελατήριο στο νήμα; Τη δύναμη που ασκεί το νήμα στη ράβδο; Τη δύναμη που ασκεί η ράβδος στο νήμα; Και η Διδακτική της Φυσικής μας λέει ότι οι διδασκόμενοι αντιμετωπίζουν σοβαρά προβλήματα στο να αναγνωρίζουν όλες αυτές τις δυνάμεις. Ποια άραγε σκοπιμότητα, από τη σκοπιά της Διδακτικής, επέβαλε να τους ζητούμε ΤΟ ΜΕΤΡΟ ΤΗΣ ΤΑΣΗΣ;

3. Το πρόβλημα αναφέρεται σε τρία φαινόμενα.

Το πρώτο από αυτά είναι η ΙΣΟΡΡΟΠΙΑ του συστήματος.

Το δεύτερο είναι η ΤΑΛΑΝΤΩΣΗ του σφαιριδίου.

Το τρίτο φαινόμενο είναι η ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ της ράβδου με το στερεωμένο στο άκρο της σφαιρίδιο.

Κατά τη μελέτη της ισορροπίας της ράβδου, με βάση το ζητούμενο, δεν ενδιαφέρει η παρουσία του ελατηρίου με το ακίνητο σφαιρίδιο. Η μοναδική συνέπεια της παρουσίας τους είναι η ενδεχόμενη δημιουργία σύγχυσης στους μαθητές.

Τα δύο άλλα φαινόμενα, η ταλάντωση δηλαδή του σφαιριδίου και η στροφική κίνηση, ΔΕΝ ΕΧΟΥΝ ΚΑΜΙΑ ΣΧΕΣΗ ΜΕΤΑΞΥ ΤΟΥΣ. Θα μπορούσαμε να έχουμε δύο διαφορετικά προβλήματα. Η συστέγασή τους έγινε για να οικοδομηθεί ένα ΠΡΟΒΛΗΜΑ ΦΥΣΙΚΗΣ , δεδομένου ότι το ΘΕΜΑ 4 οφείλει να ΣΥΝΙΣΤΆ ΠΡΟΒΛΗΜΑ. Το στοιχείο αυτό είναι και το «αδύνατο σημείο» του ΘΕΜΑΤΟΣ.