Ανδρέας Ιωάννου Κασσέτας

Η Φυσική στην Α΄ Λυκείου

Η ΔΙΔΑΣΚΑΛΙΑ 11.

Αν εκτοξεύσουμε μια πέτρα προς τα πάνω με ταχύτητα υ₀

η ΘΕΣΗ της y μετά χρόνο t θα είναι y = υ₀t – ½ gt²

ενώ η ΤΑΧΥΤΗΤΑ της θα είναι ίση με υ = υ₀ – gt

τι γίνεται εάν την

εκτοξεύσουμε οριζόντια ;

Το ερώτημα απασχόλησε

τον Γαλιλαίο

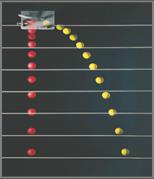
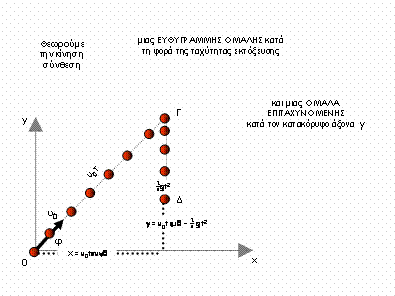
Την κίνηση που ακολουθεί μετά την οριζόντια βολή τη θεώρησε σύνθεση

α. της κίνησης που θα έκανε το αντικείμενο αν δεν υπήρχε βαρύτητα ( ΕΥΘΥΓΡΑΜΜΗΣ ΟΜΑΛΗΣ )

β. της κίνησης που θα έκανε το αντικείμενο αν δεν είχε ταχύτητα και αφηνόταν ελεύθερο

( ΟΜΑΛΑ ΕΠΙΤΑΧΥΝΟΜΕΝΗΣ με επιτάχυνση g )

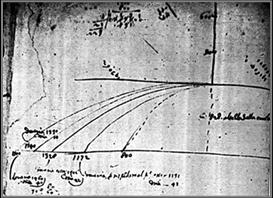
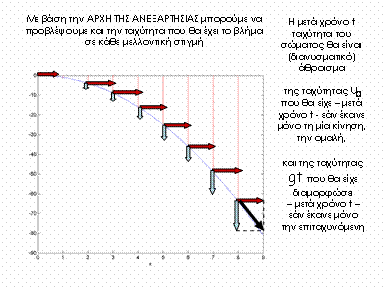
Και διατύπωσε τη λεγόμενη

ΑΡΧΗ ΤΗΣ ΑΝΕΞΑΡΤΗΣΙΑΣ των κινήσεων

Η ΚΙΝΗΣΗ που ακολουθεί μια οριζόντια βολή

είναι μια κίνηση σε επίπεδη τροχιά

και για προβλέψουμε την εξέλιξή της

θα χρειαστεί να χρησιμοποιήσουμε

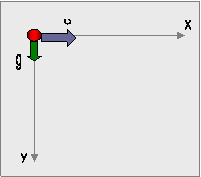
ένα ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ

με δύο ορθογώνιους άξονες

έναν οριζόντιο x και έναν κατακόρυφο y.

Ως Αρχή των αξόνων

θα θεωρήσουμε

το σημείο που γίνεται η εκτόξευση

Από τις δύο εξισώσεις x = υ₀t και y = ½ gt²

με απαλοιφή του t, προκύπτει η

y = gx²/2υ₀²

Εάν τη «δούμε» ως

ΣΥΝΑΡΤΗΣΗ y = f ( x ) - συνάρτηση δευτέρου βαθμού –

μπορούμε να φανταστούμε τη γραφική της παράσταση

το σύνολο δηλαδή των σημείων για τα οποία το x και το y συνδέονται με την

y = gx²/2υ₀²

Μπορούμε με άλλα λόγια να προβλέψουμε τη μορφή της ΤΡΟΧΙΑΣ.

Η γραμμή θα είναι μια ΠΑΡΑΒΟΛΗ

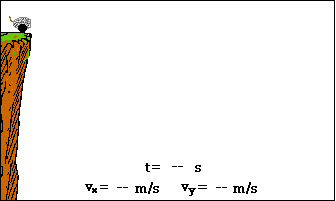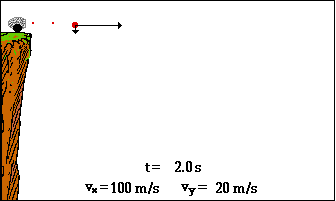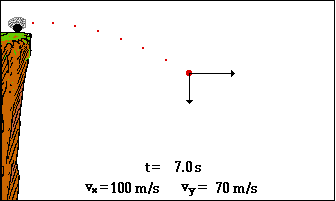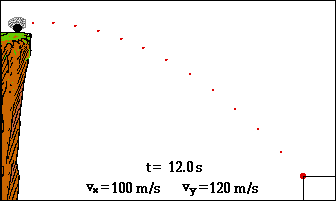
Τι γίνεται εάν

εκτοξεύσουμε

την πέτρα

πλάγια τα πάνω ;

Θα χρειαστούμε και πάλι

ένα ορθογώνιο σύστημα αναφοράς

με αρχή των αξόνων

το σημείο εκτόξευσης

και θα εφαρμόσουμε την Αρχή της Ανεξαρτησίας

Τι γίνεται

με την ΤΑΧΥΤΗΤΑ του

κατά την εξέλιξη της κίνησης ;

Η έννοια ΟΡΜΗ