Ανδρέας Ιωάννου Κασσέτας
Η Φυσική στην Α΄ Λυκείου .
Η ΔΙΔΑΣΚΑΛΙΑ
2

Εάν
το α![]() ντικείμενο μετακινείται
προς την ίδια κατεύθυνση
ντικείμενο μετακινείται
προς την ίδια κατεύθυνση
με
σταθερό ρυθμό
η
ευθύγραμμη κίνηση χαρακτηρίζεται ΟΜΑΛΗ
![]() Αυτό το
Αυτό το
«με
σταθερό ρυθμό»,
με
δυσκολεύει
Σε
κάθε δευτερόλεπτο να μετακινείται την ίδια απόσταση
![]() Αν σε κάθε ένα
δευτερόλεπτο φωτογραφίζουμε τη θέση του, όλες οι θέσεις του να ισαπέχουν
Αν σε κάθε ένα
δευτερόλεπτο φωτογραφίζουμε τη θέση του, όλες οι θέσεις του να ισαπέχουν
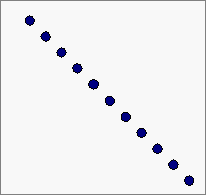 Η φωτογραφία
Η φωτογραφία
να
είναι όπως αυτή
Και
όχι όπως αυτή
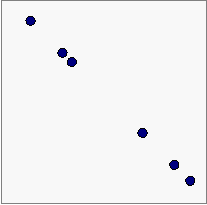
Πώς
μπορούμε στο εργαστήριο
![]() να διακρίνουμε
να διακρίνουμε
ότι
μια κίνηση είναι ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ;
Μια
καλή διάταξη που διαθέτει κάθε σχολικό εργαστήριο είναι ο χρονομετρητής με
χαρτοταινία
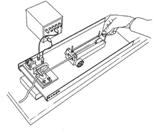
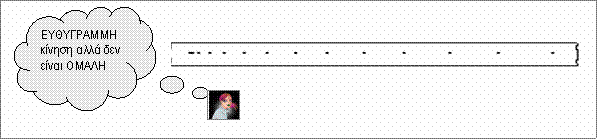
![]() Πάνω στη χαρτοταινία
μπορείς να έχεις
Πάνω στη χαρτοταινία
μπορείς να έχεις
τα
ίχνη των σημείων στα οποία βρέθηκε
το
αντικείμενο ανά ίσα χρονικά διαστήματα

Δυο λαγοί στο
δάσος. Και οι δύο τρέχουν ίσια
Ο ένας, ο Α,
μετακινείται 30 μέτρα σε 6 δευτερόλεπτα.
![]() Ο άλλος, ο Β, 48 μέτρα σε 8 δευτερόλεπτα.
Ο άλλος, ο Β, 48 μέτρα σε 8 δευτερόλεπτα.
Ποιος είναι πιο
γρήγορος ;
Να
βρούμε
![]() «πόσα μέτρα στο ΚΑΘΕ ΕΝΑ
δευτερόλεπτο »
«πόσα μέτρα στο ΚΑΘΕ ΕΝΑ
δευτερόλεπτο »
και
για τον κάθε λαγό χωριστά

![]()
![]() Ο Α κάνει 30 μέτρα στα 6 δευτερόλεπτα,
Ο Α κάνει 30 μέτρα στα 6 δευτερόλεπτα,
άρα 5 μέτρα σε κάθε δευτερόλεπτο
Αυτό το «5
μέτρα σε κάθε
δευτερόλεπτο», η Φυσική το λέει η «ΤΑΧΥΤΗΤΑ του λαγού Α είναι
5 m/s»
![]()
![]() Ο Β κάνει 48 μέτρα στα 8 δευτερόλεπτα
Ο Β κάνει 48 μέτρα στα 8 δευτερόλεπτα
άρα 6 μέτρα σε κάθε δευτερόλεπτο
Ο
λαγός Β είναι πιο γρήγορος.
![]() Σε ευθύγραμμη ομαλή κίνηση
Σε ευθύγραμμη ομαλή κίνηση
για να
υπολογίσουμε την τιμή της ταχύτητας
ενός αντικειμένου
κάνουμε ΔΙΑΙΡΕΣΗ
απόσταση στην οποία μετακινήθηκε
χρονικό διάστημα της μετακίνησης
ταχύτητα =
![]()
![]()
Σε ευθύγραμμη ομαλή κίνηση
εάν μετρήσουμε με χρονόμετρο το χρονικό
διάστημα t
από τη στιγμή που το αντικείμενο βρισκόταν στην
ΑΡΧΗ Ο
μέχρι τη στιγμή που η θέση του έγινε
x

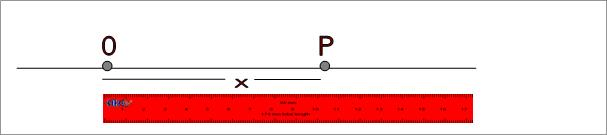
και με μετροταινία την τιμή x
και διαιρέσουμε το x με το
χρονικό διάσημα t
θα έχουμε υπολογίσει την ταχύτητα. Τη συμβολίζουμε με υ .
![]()
![]()
![]()
![]()
![]()
![]()
Αργότερα θα δούμε
ότι
η Φυσική
εμπλουτίζει την έννοια ΤΑΧΥΤΗΤΑ με ένα παράξενο τρόπο
Η περιγραφή του φαινομένου
ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ
μπορεί να γίνει σε δύο γλώσσες διαφορετικές.
Η μία
είναι γλώσσα ΑΛΓΕΒΡΑΣ
Σε ευθύγραμμη
ομαλή κίνηση κάθε υλικού σημείου
εάν επιλέξουμε ως
Αρχή των χρόνων μια χρονική στιγμή
κατά την οποία το
υλικό σημείο βρίσκεται στη Αρχή των αξόνων,
την οποία επίσης
έχουμε επιλέξει εμείς
ισχύει
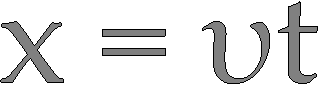
την x = υt
μπορούμε να τη
χρησιμοποιήσουμε
α. ως ΕΞΙΣΩΣΗ πρώτου βαθμού
Εάν ξέρουμε τη
θέση του x σε
μια ορισμένη χρονική στιγμή t
μπορούμε να χρησιμοποιήσουμε τη σχέση αυτή ως ΕΞΙΣΩΣΗ με άγνωστο το υ και να
υπολογίσουμε την ταχύτητά του υ = x/t
Εάν ξέρουμε την
τιμή της ταχύτητας και τη θέση του σε
μια άγνωστη χρονική στιγμή μπορούμε να χρησιμοποιήσουμε τη σχέση αυτή ως
ΕΞΙΣΩΣΗ με άγνωστο το t και να προσδιορίσουμε την άγνωστη χρονική
στιγμή t = x / υ
β . ως ΣΥΝΑΡΤΗΣΗ x
= υt
Εάν ξέρουμε την
ταχύτητα του κινητού, η σχέση αυτή μας
λέει «που θα βρίσκεται»
- ποια θα είναι η ΘΕΣΗ του – σε κάθε ΧΡΟΝΙΚΗ
ΣΤΙΓΜΗ του μέλλοντος
H άλλη είναι γλώσσα ΓΕΩΜΕΤΡΙΑΣ
Το 1637, εποχή που ο Γαλιλαίος έχει ήδη δικαστεί
 και καταδικαστεί
και καταδικαστεί
από την
Ιερά Εξέταση
και ο Νεύτων
δεν έχει ακόμα γεννηθεί ,
στη Γαλλία ο Descartes
– που τον λέμε
και ΚΑΡΤΕΣΙΟ –
κάνει
μια
εντυπωσιακή πρόταση
Η πρότασή του, η οποία θα αποδειχθεί ιδιαίτερα γόνιμη
για τη Φυσική,
περιέχει την
ΙΔΕΑ ότι ΚΑΘΕ ΑΛΓΕΒΡΙΚΗ ΣΥΝΑΡΤΗΣΗ
έχει μια
δική της ΕΙΚΟΝΑ,
σε ένα ειδικό σύστημα αξόνων.
Την εικόνα της
αυτή, τη λέμε ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
Η ΑΛΓΕΒΡΙΚΗ
συνάρτηση y
= x2
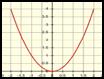 γίνεται
γίνεται
ΓΕΩΜΕΤΡΙΚΗ
εικόνα
![]() Και
τι σχέση αυτό, με το φαινόμενο
Και
τι σχέση αυτό, με το φαινόμενο
ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ ;
![]() Εφόσον τη σχέση x = υt τη βλέπουμε ως ΣΥΝΑΡΤΗΣΗ x = υt
Εφόσον τη σχέση x = υt τη βλέπουμε ως ΣΥΝΑΡΤΗΣΗ x = υt
η κίνηση περιγράφεται με τη ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
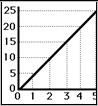 της
συνάρτησης των τιμών θέσης και χρονικής στιγμής
της
συνάρτησης των τιμών θέσης και χρονικής στιγμής
Μια ευθύγραμμη
ομαλή κίνηση
με ταχύτητα 5 m / s
περιγράφεται
με τηνεικόνα
Σε κάθε
ευθύγραμμη ομαλή κίνηση μπορούμε να δημιουργούμε μια ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
με την οποία
ΠΕΡΙΓΡΑΦΕΤΑΙ η κίνηση εξίσου αποτελεσματικά όσο και με την
ΑΛΓΕΒΡΙΚΗ ΣΥΝΑΡΤΗΣΗ x =
υt
Διαπιστώνεται ότι
εάν η ευθύγραμμη κίνηση είναι και ΟΜΑΛΗ,
η γραφική
παράσταση είναι μια ΕΥΘΕΙΑ
και εάν η γραφική
παράσταση μιας ευθύγραμμης κίνησης είναι
ΕΥΘΕΙΑ,
η κίνηση θα είναι
ΟΜΑΛΗ
![]() η έννοια ΤΑΧΥΤΗΤΑ
η έννοια ΤΑΧΥΤΗΤΑ
περιγράφει
τον ΡΥΘΜΟ ΜΕΤΑΒΟΛΗΣ ΤΗΣ ΘΕΣΗΣ
δηλαδή το « πόσο γρήγορα αλλάζει η θέση»
Αν ο ρυθμός
μεταβολής της θέσης είναι σταθερός,
η ταχύτητα ορίζεται από τη σχέση
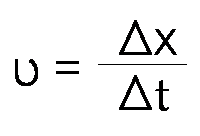
![]() τι είναι
τι είναι
αυτό το Δx ;
Σε μια ευθύγραμμη
κίνηση, το Δx -
η λεγόμενη «ΜΕΤΑΤΟΠΙΣΗ» -
![]() παριστάνει τη διαφορά x2 – x1 η οποία παρατηρήθηκε στη θέση του κινητού
παριστάνει τη διαφορά x2 – x1 η οποία παρατηρήθηκε στη θέση του κινητού
– η θέση ήταν x1 και έγινε x2 -
το Δt παριστάνει το χρονικό διάστημα
στο οποίο
παρατηρήθηκε η μετατόπιση
Κατά την
ευθύγραμμη ομαλή κίνηση εφόσον η ταχύτητα είναι σταθερή
η γραφική
παράσταση ταχύτητας - χρόνου θα είναι
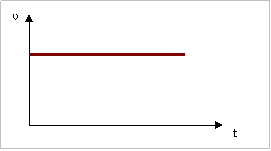
|
Το γινόμενο « ταχύτητα επί χρόνος » |
|
|
Σύμφωνα με τη
Φυσική είναι η ΘΕΣΗ του
κινητού και γενικότερα η μετατόπισή
του . |
Σύμφωνα με τη
ΓΕΩΜΕΤΡΙΑ το ίδιο αυτό γινόμενο είναι ίσο με το ΕΜΒΑΔΟΝ του παραλληλογράμμου
που δημιουργείται κάτω από το γράφημα ταχύτητας χρόνου |

Το ΕΜΒΑΔΟΝ του παραλληλογράμμου
που δημιουργείται
κάτω από το γράφημα ταχύτητας χρόνου
είναι ίσο με τη
ΜΕΤΑΤΟΠΙΣΗ του αντικειμένου σε μια ευθύγραμμη ομαλή κίνηση

Το δεύτερο από τα
ΦΑΙΝΟΜΕΝΑ που θα μας απασχολήσουν είναι μια ακόμα ΚΙΝΗΣΗ.
![]() σημειακού αντικειμένου.
σημειακού αντικειμένου.
Είναι κι αυτή ευθύγραμμη
αλλά η ταχύτητα του σώματος δεν είναι σταθερή.
Αυξάνεται συνεχώς
και μάλιστα με σταθερό ρυθμό,
 κάθε δηλαδή δευτερόλεπτο αυξάνεται κατά
τον ίδιο ποσό.
κάθε δηλαδή δευτερόλεπτο αυξάνεται κατά
τον ίδιο ποσό.
Το
αντικείμενο
ήταν ακίνητο
και σε κάποια χρονική στιγμή
ξεκίνησε.
Αρχίζω να
ενδιαφέρομαι για αυτό από τη στιγμή εκείνη.
Κινείται ίσια και ένα δευτερόλεπτο μετά την εκκίνηση
η ταχύτητά του είναι 3 m/s,
στο τέλος του
δεύτερου δευτερολέπτου 6 m/s ,
στο τέλος του
τρίτου, 9 m/s,
στο τέλος του
τέταρτου 12 m/s .

ΛΕΜΕ:
« η ΕΠΙΤΑΧΥΝΣΗ
του αντικειμένου είναι «3 μέτρα ανά δευτερόλεπτο, σε κάθε δευτερόλεπτο»
και ΓΡΑΦΟΥΜΕ
α = 3 m/s2
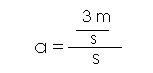
Εφόσον η ταχύτητα
του σώματος σε ΚΑΘΕ ένα δευτερόλεπτο
αυξάνεται κατά 3 μονάδες
η επιτάχυνση με άλλα λόγια είναι 3m/s2 - ,
μπορούμε να συμπεράνουμε ότι
μετά από t
δευτερόλεπτα η ταχύτητα θα είναι 3t.
Γενικότερα,
ΤΑΧΥΤΗΤΑ = ΕΠΙΤΑΧΥΝΣΗ επί ΧΡΟΝΟΣ
ή με σύμβολα
υ = α t
Με την προϋπόθεση ότι
στην Αρχή των χρόνων
![]() βρισκόταν στην Αρχή των
αξόνων αποδεικνύεται
βρισκόταν στην Αρχή των
αξόνων αποδεικνύεται
ότι για τη ΘΕΣΗ του, x, στο μέλλον
- σε χρονικό διάστημα t από την αρχή των χρόνων-
, ισχύει
x = ½αt2
 Στην καινούρια εξίσωση
Στην καινούρια εξίσωση
μου κάνει εντύπωση αυτό
το κλάσμα, το ½ . Πώς βρέθηκε εκεί;
![]() Αν δούμε
Αν δούμε
τη σχέση υ = αt
ως συνάρτηση υ = αt
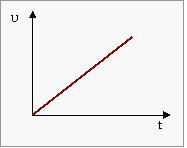 και κάνουμε
και κάνουμε
τη
γραφική
της
παράσταση
θα είναι
Στην ευθύγραμμη
ομαλή κίνηση είχαμε πει κάτι
![]() για το
ΕΜΒΑΔΟΝ του σχήματος
για το
ΕΜΒΑΔΟΝ του σχήματος
που δημιουργείται
κάτω από το γράφημα ταχύτητας χρόνου
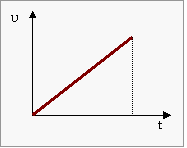 Ότι είναι ίσο με τη μετατόπιση
Ότι είναι ίσο με τη μετατόπιση
του αντικειμένου
 σε μια ευθύγραμμη
σε μια ευθύγραμμη
ομαλή κίνηση.
Τώρα όμως η
κίνηση
δεν είναι ομαλή
και το σχήμα
δεν είναι
παραλληλόγραμμο, είναι
ΤΡΙΓΩΝΟ
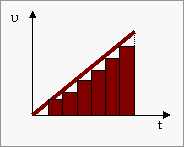 Αν το τρίγωνο το κόψεις
Αν το τρίγωνο το κόψεις
σε λεπτές φέτες
παραλληλόγραμμα
–
καθένα
από τα οποία
–
θα
είναι και μια μετατόπιση –
το
άθροισμα των εμβαδών
των
παραλληλογράμμων
θα
είναι σχεδόν ίσο με το εμβαδόν του τριγώνου
 Ναι αλλά πάντα κάτι
περισσεύει,
Ναι αλλά πάντα κάτι
περισσεύει,
υπάρχει
μια διαφορά ανάμεσα
στο
εμβαδόν του τριγώνου
και
στο άθροισμα των εμβαδών
![]() Αν το ξανακάνεις με πολύ πολύ πολύ λεπτές
φέτες,
Αν το ξανακάνεις με πολύ πολύ πολύ λεπτές
φέτες,
αυτή η διαφορά θα
ελαττώνεται
Οι μαθηματικοί
θεωρούν ότι
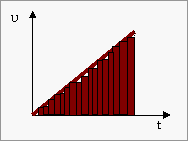 τελικά το εμβαδόν του σχήματος
τελικά το εμβαδόν του σχήματος
σε μια τυχαία
ευθύγραμμη κίνηση
θα είναι ίσο με
τη θέση και γενικότερα
με τη μετατόπιση.
Στην ομαλά επιταχυνόμενη
κίνηση
είναι εμβαδόν ενός τριγώνου
![]() Τώρα κατάλαβα που βρέθηκε το ½ . .
Τώρα κατάλαβα που βρέθηκε το ½ . .
Το εμβαδόν του
τριγώνου
είναι «½ βάση επί
ύψος»
άρα x = ½ t. at
= ½at2
![]()
![]() Μονάδα μέτρησης της επιτάχυνσης είναι
το 1 m/s2
Μονάδα μέτρησης της επιτάχυνσης είναι
το 1 m/s2
Πόσο είναι 1 m/s2 ;
είναι μεγάλη επιτάχυνση ;
 Μικρότερη
Μικρότερη
από
την επιτάχυνση
μιας μοτοσικλέτας
;
του Usain Bolt
;
Μια
μικρή σχετικά μοτοσικλέτα Yamaha YZF
R15
πιάνει
τα 100 km/h σε 14 s .
Εφόσον
![]() 100 km/h =
100000 m/ 3600s = 27,77 m/s ,
100 km/h =
100000 m/ 3600s = 27,77 m/s ,
η επιτάχυνσή της είναι περίπου 2 m/s2
Τόση περίπου, ίσως και λίγο μεγαλύτερη, ήταν
 και
η
και
η
επιτάχυνση του Usain Bolt
στα πρώτα
δευτερόλεπτα της
διαδρομής που κατέρριψε
το παγκόσμιο ρεκόρ
των 200 μέτρων
![]()
Τι γίνεται με τα
αυτοκίνητα ;
 το Mitsubishi Colt 2007
το Mitsubishi Colt 2007
πιάνει
τα 100 km/h
σε 12,9 s
α = 2,15 m/s2
 το HYUNDAI elantra
το HYUNDAI elantra
πιάνει
τα 100 km/h
σε 13,8 s
α = 1,97
m/s2
 το Fiat Punto
1,3 2003
το Fiat Punto
1,3 2003
πιάνει
τα 100 km/h
σε 13,2 s
α = 2,1 m/s2
 το Citroen Xsara
το Citroen Xsara
πιάνει
τα 100 km/h
σε 10,02 s
α = 2,77 m/s2
 το Peugeot 107
το Peugeot 107
πιάνει
τα 100 km/h
σε 10,7 s
α = 2,6 m/s2
 το
Porsche Carrera GT
το
Porsche Carrera GT
σε 11, 3 s
πιάνει
211 km/h
α = 5,18 m/s2
![]() Ίσως η πιο μεγάλη επιτάχυνση
Ίσως η πιο μεγάλη επιτάχυνση
που έχω δει
είναι εκείνη με
τα οχήματα στους
αγώνες
 Formula 1.
Formula 1.
Είναι μεγαλύτερη
και από της
Porsche Carrera GT
Η πιο μεγάλη
επιτάχυνση
![]() που έχεις «συναντήσει»
που έχεις «συναντήσει»
εκδηλώνεται
σε μια κίνηση
 που τη βλέπεις καθημερινά
που τη βλέπεις καθημερινά
από τότε που
ήσουνα μικρός .
Αν η Porsche
έχει επιτάχυνση
5,2 m/s2
και η Ferrari 6,5 m/s2
η κίνηση κάθε πέτρας
που πέφτει στο
έδαφος
γίνεται με
επιτάχυνση 9,8 m/s2
Θα το συζητήσουμε
αργότερα
Να συνοψίσουμε
![]() Το γεγονός ότι το αντικείμενο
Το γεγονός ότι το αντικείμενο
αλλάζει
συνεχώς θέση μας
κάνει να λέμε ότι
το φαινόμενο είναι

το ότι το
αντικείμενο πηγαίνει ίσια χωρίς
καθόλου να
στρίβει μας κάνει να χαρακτηρίζουμε την κίνηση

και το ότι η
ταχύτητα αυξάνεται με σταθερό ρυθμό
μας κάνει την χαρακτηρίζουμε

Η περιγραφή της μπορεί
να γίνει
σε δύο διαφορετικές γλώσσες
Η μία είναι
γλώσσα ΑΛΓΕΒΡΑΣ
x
= ½αt2
υ = αt
η άλλη είναι γλώσσα ΓΕΩΜΕΤΡΙΑΣ
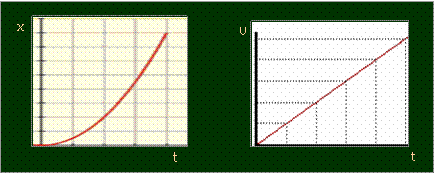
Συνοψίζουμε
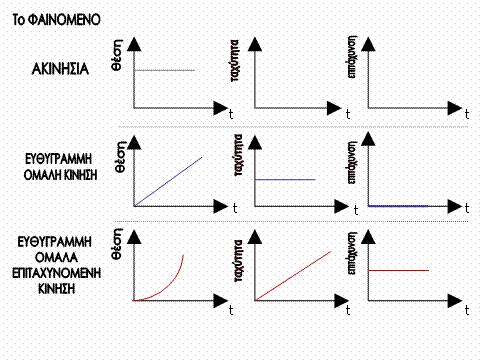
Συνέχεια