Ανδρέας Ιωάννου Κασσέτας

Η Φυσική στη B΄ Γυμνασίου.

Η ΔΙΔΑΣΚΑΛΙΑ 2 .

Το πρώτο από τα ΦΑΙΝΟΜΕΝΑ που θα μας απασχολήσουν είναι

η ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ

Και αρχικά το μόνο που μας ζητείται να κάνουμε γι αυτό είναι να το ΠΕΡΙΓΡΑΨΟΥΜΕ

Αργότερα θα αναρωτηθούμε και για το «πώς» μπορούμε

να το ΕΡΜΗΝΕΥΟΥΜΕ και να το ΠΡΟΒΛΕΠΟΥΜΕ

Το κινούμενο ΑΝΤΙΚΕΙΜΕΝΟ μπορεί να είναι μια μικρή μπίλια, μια σταγόνα βροχής, μια αθερίνα στη θάλασσα

η άκρη του τιμονιού ενός ποδήλατου, ένα μυρμήγκι,

Για να μπορέσουμε να περιγράψουμε την κίνησή του, αγνοούμε τις διαστάσεις του.

Το φανταζόμαστε δηλαδή

κάθε στιγμή να «χωράει» σε ένα γεωμετρικό σημείο και
το κινούμενο αυτό

αντικείμενο

το χαρακτηρίζουμε

«σημειακό αντικείμενο»

ή «υλικό σημείο»

Παρατηρούμε ότι

καθώς

κυλάει ο χρόνος

το αντικείμενο

αλλάζει συνεχώς θέση

αλλά και κινείται ΙΣΙΑ

προς την ίδια πάντα

κατεύθυνση, χωρίς να στρίβει

Όλα τα γεωμετρικά σημεία από τα οποία πέρασε βρίσκονται σε μία ΓΡΑΜΜΗ. Είναι η ΤΡΟΧΙΑ του .

Εφόσον κινείται ίσια η τροχιά του θα είναι μία ΕΥΘΕΙΑ ΓΡΑΜΜΗ

Το φαινόμενο λέγεται ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ

Για να περιγράψουμε το φαινόμενο χρησιμοποιούμε τις έννοιες

ΘΕΣΗ, ΧΡΟΝΟΣ και ΤΑΧΥΤΗΤΑ.

Τον ΧΡΟΝΟ που διαρκεί «κάποιο φαινόμενοι» τον λέμε και ΧΡΟΝΙΚΟ ΔΙΑΣΤΗΜΑ .

Τον συμβολίζουμε με το γράμμα t

Τον μετράμε με χρονόμετρο. Ως μονάδα μέτρησης

η Φυσική χρησιμοποιεί το ένα δευτερόλεπτο. Γράφουμε 1 s

Τι λέγεται

«ένα δευτερόλεπτο» ;

Ο ορισμός της μονάδας 1 s

βασίστηκε

στην κίνηση του πλανήτη Γη.

ΤΟ ΔΕΥΤΕΡΟΛΕΠΤΟ

δηλαδή ορίστηκε

ως το 1/86400

της διάρκειας μιας περιστροφή

της Γης .

Εδώ και μερικές δεκαετίες

ο άλλαξε ο τρόπος που ορίζεται

χωρίς όμως να αλλάξει

η ποσότητα χρόνου στην οποία αντιστοιχεί

Με το χρονόμετρο μετράμε

ένα χρονικό διάστημα.

Συχνά όμως λέμε ότι

« αυτό συνέβη εκείνη τη χρονική στιγμή» .

Τι γίνεται με τη ΧΡΟΝΙΚΗ ΣΤΙΓΜΗ ;

Η χρονική στιγμή δεν έχει διάρκεια .

Είναι όπως ένα σημείο της Γεωμετρίας

που δεν «πιάνει καθόλου χώρο»

Ενώ το χρονικό διάστημα απαντά στο ερώτημα

« ΠΟΣΟ ΔΙΑΡΚΕΙ ;»

η χρονική στιγμή απαντά στο «ΠΟΤΕ;»

Για μένα η ΧΡΟΝΙΚΗ ΣΤΙΓΜΗ είναι «ασύληπτη» .

Υπάρχει κι ύστερα δεν υπάρχει

Πώς μπορούμε να τη μετρήσουμε ;

Τη χρονική στιγμή δεν τη μετράμε,αλλά μπορούμε να την προσδιορίσουμε

Για να την προσδιορίσουμε κάνουμε μια συμφωνία .

Θεωρούμε μια ορισμένη χρονική στιγμή, ας πούμε την «μεσάνυχτα», ως Αρχή των χρόνων.

Στη συνέχεια μετράμε το χρονικό διάστημα από τα μεσάνυχτα μέχρι τώρα.

Αν τη χρονική αυτή διάρκεια τη βρούμε 7 ώρες, είκοσι λεπτά και 3 δευτερόλεπτα ώρες

λέμε ότι τώρα είναι « 7 h 20 min 3 s ή 7.20.03 »

Αυτός που περιγράφει

μια κίνηση μπορεί να διαλέγει

όποια στιγμή θέλει ως Αρχή των χρόνων;

Μπορεί

να επιλέγει

οποιαδήποτε .

Την απόσταση δύο γεωμετρικών σημείων

τη μετράμε με μετροταινία

Γι α μικρές αποστάσεις μας εξυπηρετεί και το υποδεκάμετρο είναι

Ως μονάδα μέτρησης

η Φυσική χρησιμοποιεί το ένα μέτρο «των Γάλλων» . Γράφουμε 1 m

Τι θα πει

«το ένα μέτρο των Γάλλων» ;

Την περίοδο της Γαλλικής Επανάστασης ξεκίνησε μια προσπάθεια για την καθιέρωση μονάδων μέτρησης που θα ίσχυαν

για όλους τους λαούς και σε όλες τις εποχές

Το 1791 η Γαλλική Εθνοσυνέλευση όρισε μια επιτροπή από επιστήμονες

για να μελετήσει το πρόβλημα.

Στο ζήτημα της μονάδας μήκους

η άποψη που κυριάρχησε ήταν η νέα μονάδα

- για να μπορεί να γίνει παγκόσμια αποδεκτή –

να βασίζεται

στο μέγεθος του πλανήτη Γη .

Μια ειδική αποστολή

ανέλαβε να μετρήσει

την απόσταση Δουνκέρκης - Βαρκελώνης

πάνω στον μεσημβρινό

που περνάει από το Αστεροσκοπείο του Παρισιού.

απόσταση μετρήθηκε,

ύστερα από οκτώ χρόνια,

και με τη βοήθεια του πολικού αστέρα υπολογίστηκε

η απόσταση Βόρειου Πόλου – Ισημερινού

Ένα βολικό κλάσμα

της απόστασης αυτής

-το ένα προς 10.000.000 -ορίστηκε ως η νέα μονάδα μήκους που ονομάστηκε « 1 mètre ».

Εδώ και μερικές δεκαετίες άλλαξε ο τρόπος που ορίζεται χωρίς όμως

να αλλάξει η «ποσότητα απόστασης» στην οποία αντιστοιχεί

Παρατηρούμε ένα αυτοκίνητο που τρέχει
και θέλουμε να απαντήσουμε στο ερώτημα
«που βρίσκεται;»
σε κάποια στιγμή .

Μια σκέψη είναι να βρούμε «πόσο απέχει»

από ένα σημείο που θα έχουμε συμφωνήσει να είναι η Αρχή.
Από μια κολώνα λόγου χάρη.

Αν ξέρουμε ότι
«τη στιγμή αυτή απέχει από την κολώνα 26 μέτρα»

σημαίνει ότι ξέρουμε τη στιγμή εκείνη τη θέση του .
Την επόμενη στιγμή η θέση του θα είναι διαφορετική

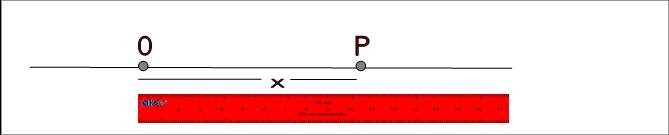
Η απόσταση του γεωμετρικού σημείου Ρ στο οποίο βρίσκεται «τώρα»
από το γεωμετρικό σημείο Ο - το οποίο έχουμε συμφωνήσει να το θεωρούμε «Αρχή τωναξόνων» –

είναι η ΘΕΣΗ του αντικειμένου . Τη συμβολίζουμε με το γράμμα x.

Κάθε στιγμή το κινούμενο αντικείμενο βρίσκεται σε ένα σημείο διαφορετικό.
Τη στιγμή που βρίσκεται σε σημείο τέτοιο που να απέχει 7 μέτρα από την Αρχή Ο

λέμε ότι η ΘΕΣΗ του είναι 7 μέτρα και γράφουμε x = 7 m.

Μια επόμενη στιγμή που απέχει - από το Ο- 11 μέτρα

λέμε ότι η ΘΕΣΗ του είναι 11μέτρα και γράφουμε x = 11 m

Κατανοούμε επίσης ότι στο χρονικό διάστημα από τη μια στιγμή στην άλλη το αντικείμενο μετακινήθηκε κατά 4 μέτρα

Αν κατάλαβα καλά

η ΑΠΟΣΤΑΣΗ απαντά στο «πόσο απέχουν δύο σημεία ;» και τη ΜΕΤΡΑΜΕ με μια μετροταινία

Ενώ η ΘΕΣΗ απαντά στο « που βρίσκεται ένα σημείο;» και την ΠΡΟΣΔΙΟΡΙΖΟΥΜΕ ,

σε σχέση με μία Αρχή, αφού μετρήσουμε την απόσταση από την Αρχή

Έχεις καταλάβει

πάρα πολύ καλά

η ΑΠΟΣΤΑΣΗ απαντά στο «πόσο απέχουν δύο σημεία ;» και τη ΜΕΤΡΑΜΕ με μια μετροταινία	Το ΧΡΟΝΙΚΟ ΔΙΑΣΤΗΜΑ απαντά στο «πόσο διαρκεί» και το ΜΕΤΡΑΜΕ με χρονόμετρο
η ΘΕΣΗ απαντά στο « που βρίσκεται ένα σημείο;» και την ΠΡΟΣΔΙΟΡΙΖΟΥΜΕ , σε σχέση με μία Αρχή, αφού μετρήσουμε την απόσταση από την Αρχή	Ενώ η ΧΡΟΝΙΚΗ ΣΤΙΓΜΗ απαντά στο « πότε ;» και την ΠΡΟΣΔΙΟΡΙΖΟΥΜΕ σε σχέση με μία Αρχή των χρόνων, αφού μετρήσουμε το χρονικό διάστημα από την Αρχή

Εάν το αντικείμενο μετακινείται προς την ίδια κατεύθυνση

με σταθερό ρυθμό

η ευθύγραμμη κίνηση χαρακτηρίζεται ΟΜΑΛΗ

Αυτό το

«με σταθερό ρυθμό»

με δυσκολεύει

Σε κάθε δευτερόλεπτο να μετακινείται την ίδια απόσταση

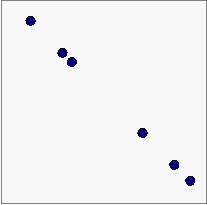
Αν σε κάθε ένα δευτερόλεπτο φωτογραφίζουμε τη θέση του, όλες οι θέσεις του να ισαπέχουν

Η φωτογραφία

να είναι όπως αυτή

Και όχι όπως αυτή

Πώς μπορούμε στο εργαστήριο

να διακρίνουμε

ότι μια κίνηση είναι ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ;

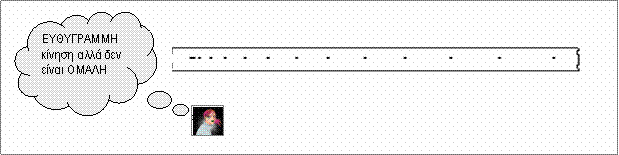
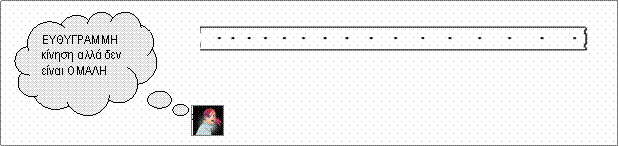
Μια καλή διάταξη που διαθέτει κάθε σχολικό εργαστήριο είναι ο χρονομετρητής με χαρτοταινία

Πάνω στη χαρτοταινία μπορείς να έχεις

τα ίχνη των σημείων στα οποία βρέθηκε

το αντικείμενο ανά ίσα χρονικά διαστήματα

Δυο λαγοί στο δάσος. Και οι δύο τρέχουν ίσια

Ο ένας, ο Α, μετακινείται 30 μέτρα σε 6 δευτερόλεπτα.

Ο άλλος, ο Β, 48 μέτρα σε 8 δευτερόλεπτα.

Ποιος είναι πιο γρήγορος ;

Να βρούμε

«πόσα μέτρα στο ΚΑΘΕ ΕΝΑ δευτερόλεπτο »

και για τον κάθε λαγό χωριστά

Ο Α κάνει 30 μέτρα στα 6 δευτερόλεπτα,

άρα 5 μέτρα σε κάθε δευτερόλεπτο

	Αυτό το «5 μέτρα σε κάθε δευτερόλεπτο», η Φυσική το λέει η «ΤΑΧΥΤΗΤΑ του λαγού Α είναι 5 m/s»

Ο Β κάνει. 48 μέτρα στα 8 δευτερόλεπτα

άρα 6 μέτρα σε κάθε δευτερόλεπτο

Ο λαγός Β είναι πιο γρήγορος.

Σε ευθύγραμμη ομαλή κίνηση

για να υπολογίσουμε την τιμή της ταχύτητας

ενός αντικειμένου

κάνουμε ΔΙΑΙΡΕΣΗ

απόσταση στην οποία μετακινήθηκε

χρονικό διάστημα της μετακίνησης

ταχύτητα =

Σε ευθύγραμμη ομαλή κίνηση

εάν μετρήσουμε με χρονόμετρο το χρονικό διάστημα t

από τη στιγμή που το αντικείμενο βρισκόταν στην ΑΡΧΗ Ο

μέχρι τη στιγμή που η θέση του έγινε x

και με μετροταινία την τιμή x

και διαιρέσουμε το x με το χρονικό διάσημα t

θα έχουμε υπολογίσει την ταχύτητα. Τη συμβολίζουμε με υ .

Η περιγραφή του φαινομένου

ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ

μπορεί να γίνει σε δύο γλώσσες διαφορετικές.

Η μία είναι γλώσσα ΑΛΓΕΒΡΑΣ

Στην ευθύγραμμη ομαλή κίνηση

Εφόσον το κινούμενο αντικείμενο στην Αρχή των χρόνων

βρίσκεται στην Αρχή των αξόνων, ισχύει

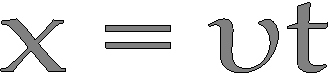
Εάν ξέρουμε την ταχύτητά του, η σχέση αυτή μας λέει «που θα βρίσκεται» -

ποια θα είναι η ΘΕΣΗ του – σε κάθε ΧΡΟΝΙΚΗ ΣΤΙΓΜΗ του μέλλοντος

Εάν ξέρουμε τη θέση του x σε μια ορισμένη χρονική στιγμή t

μπορούμε να χρησιμοποιήσουμε τη σχέση αυτή

ως ΕΞΙΣΩΣΗ με άγνωστο το υ και να υπολογίσουμε την ταχύτητά του υ = x/t

Εάν ξέρουμε την τιμή της ταχύτητας και τη θέση του

σε μια άγνωστη χρονική στιγμή μπορούμε να χρησιμοποιήσουμε

τη σχέση αυτή ως ΕΞΙΣΩΣΗ με άγνωστο το t

και να προσδιορίσουμε την άγνωστη χρονική στιγμή t = x / υ

Η άλλη είναι γλώσσα ΓΕΩΜΕΤΡΙΑΣ

Η κίνηση δηλαδή περιγράφεται με τη

ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ

θέσης και χρονικής στιγμής

Δηλαδή τι ;

Αν δύο δευτερόλεπτα από τη στιγμή που πατήσαμε το κουμπί του χρονομέτρου η θέση του αντικειμένου είναι 10 m, το ζευγάρι τιμών { 10 m, 2 s} μπορούμε να το απεικονίσουμε με ένα γεωμετρικό σημείο. Σχεδιάζουμε δύο άξονες, τον έναν με τιμές θέσης και τον άλλο με τιμέ ς χρονικής στιγμής και στο σημείο 2s του άξονα των χρονικών στιγμών φέρουμε κάθετο και στο σημείο 10 m του άξονα των θέσεων φέρνουμε επίσης κάθετο . Το σημείο Α στο οποίο τέμνονται οι δύο αυτές κάθετες είναι το σημείο που απεικονίζει το ζευγάρι τιμών { 10 m, 2 s}.

Κάνουμε το ίδιο με ένα άλλο και με άλλα ζευγάρι τιμών, όπως λόγου χάρη το { 20 m, 4 s} το οποίο απεικονίζεται με το γεωμετρικό σημείο Β και συνεχίζουμε και με άλλα ζευγάρια.

Το σύνολο των γεωμετρικών αυτών σημείων είναι μια ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ του φαινομένου

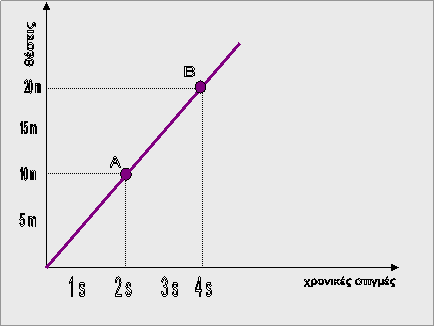
Διαπιστώνεται ότι εάν η ευθύγραμμη κίνηση είναι και ΟΜΑΛΗ,

η γραφική παράσταση είναι μια ΕΥΘΕΙΑ

Αν σε μια ευθύγραμμη κίνηση

η ταχύτητα είναι σταθερή και ίση με 5 m/s , η

είναι μια εικόνα της κίνησης είναι η γραφική παράσταση

Σε κάθε ευθύγραμμη ομαλή κίνηση

μπορούμε να δημιουργούμε μια ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ

με την οποία ΠΕΡΙΓΡΑΦΕΤΑΙ

η κίνηση εξίσου αποτελεσματικά

όσο και με την ΑΛΓΕΒΡΙΚΗ ΣΧΕΣΗ x = υt

ΜΕΤΑΒΑΛΛΟΜΕΝΗ ΚΙΝΗΣΗ θα μπορούσε να είναι

Μια ευθύγραμμη κίνηση κατά την εξέλιξη της οποίας το αντικείμενο,

χωρίς να αλλάζει κατεύθυνση, κινείται
όλο και πιο γρήγορα οπότε λέμε ότι η ταχύτητά του ΑΥΞΑΝΕΤΑΙ ή
όλο και πιο αργά, οπότε λέμε ότι η ταχύτητά του ΕΛΑΤΤΩΝΕΤΑΙ

Όταν το αντικείμενο ΔΕΝ κινείται σε ευθεία ;

Σύμφωνα με τη Φυσική

Κάθε κίνηση που ΔΕΝ είναι ευθύγραμμη
θεωρείται ΜΕΤΑΒΑΛΛΟΜΕΝΗ.

Αν ένα σημειακό αντικείμενο κινείται σε κυκλική τροχιά

χωρίς να αυξομειώνεται η ταχύτητά του η κίνησή του

θεωρείται μεταβαλλόμενη διότι ΑΛΛΑΖΕΙ ΚΑΤΕΥΘΥΝΣΗ

Αφού όμως δεν αυξομειώνεται
η ταχύτητά του
σημαίνει ότι είναι ΣΤΑΘΕΡΗ.

Οι φυσικοί δέχτηκαν ότι η ταχύτητα εκτός από μια τιμή έχει και μια ΚΑΤΕΥΘΥΝΣΗ .

Και εφόσον η κατεύθυνση αλλάζει θεωρούν ότι η ταχύτητα μεταβάλλεται

Μου είναι ιδιαίτερα δύσκολο να παραδεχτώ ότι μια ταχύτητα που είναι συνεχώς

8m/s, 8m/s, 8m/s, 8m/s, 8m/s, 8m/s, είναι «ταχύτητα που αλλάζει»

Αλλάζει εφόσον αλλάζει η κατεύθυνσή της κι ας είναι

η τιμή της συνεχώς 8 m/s.

Για τη φυσική η ταχύτητα ενός σώματος δεν απαντά μόνο στο «πόσο γρήγορα κινείται;» ,

αλλά και στο «προς τα που κινείται».

Η ταχύτητα των φυσικών ανήκει στα λεγόμενα ΔΙΑΝΥΣΜΑΤΙΚΑ ΜΕΓΕΘΗ

Την παριστάνουν μάλιστα με ένα βελάκι που το λένε διάνυσμα.

Με αυτό περιγράφεται σε κάθε στιγμή και η κατεύθυνση της.

Έτσι για τη Φυσική η ΤΑΧΥΤΗΤΑ ενός σώματος θεωρείται ΣΤΑΘΕΡΗ μόνον εφόσον διατηρείται αναλλοίωτη τόσο η τιμή της όσο και η κατεύθυνση της. Αυτό σημαίνει ότι η ταχύτητα θεωρείται ΣΤΑΘΕΡΗ ΜΟΝΟ ΣΤΗΝ ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ. ΣΕ ΚΑΘΕ ΑΛΛΗ ΚΙΝΗΣΗ, σύμφωαν με τη Φυσική η ταχύτητα ΜΕΤΑΒΑΛΛΕΤΑΙ.

Συνέχεια

η έννοια ΔΥΝΑΜΗ

.