ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ΄ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ

ΚΑΙ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ΄ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β΄)

ΤΕΤΑΡΤΗ 26 ΜΑΪΟΥ 2010

ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ

ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ( ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)

ΘΕΜΑ Α

Στις ημιτελείς προτάσεις Α1- Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά

Α1. Σε μια φθίνουσα ταλάντωση στην οποία η δύναμη απόσβεσης είναι ανάλογη της ταχύτητας του σώματος,

με την πάροδο του χρόνου

α. η περίοδος μειώνεται

β. η περίοδος είναι σταθερή

γ. το πλάτος διατηρείται σταθερό

δ. η ενέργεια ταλάντωσης διατηρείται σταθερή (Μονάδες 5)

Α2. Τα ηλεκτρομαγνητικά κύματα

α. διαδίδονται σε όλα τα υλικά με την ίδια ταχύτητα

β. έχουν στο κενό την ίδια συχνότητα

γ. διαδίδονται στο κενό με την ίδια ταχύτητα

δ. είναι διαμήκη (Μονάδες 5)

Α3. Μεταξύ δύο διαδοχικών δεσμών στάσιμου κύματος τα σημεία του ελαστικού μέσου

α . έχουν το ίδιο πλάτος ταλάντωσης

β. έχουν την ίδια φάση

γ. διαδίδονανται στο κενό με την ίδια ταχύτητα

δ. είναι διαμήκη (Μονάδες 5)

Α4. Διακρότημα δημιουργείται κατά τη σύνθεση δύο απλών αρμονικών ταλαντώσεων οι οποίες πραγματοποιούνται

στην ίδια διεύθυνση και γύρω από την ίδια θέση ισορροπίας, όταν οι δύο ταλαντώσεις έχουν

α. ίσα πλατη και ίσες συχνότητες

β. άνισα πλάτη και ίσες συχνότητες

γ. ίσα πλάτη και παραπλήσιες συχνότητες

δ. ίσα πλάτη και συχνότητες εκ των οποίων η μία είναι πολλαπλάσια της άλλης (Μονάδες 5)

Α5. Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα τη λέξη Σωστό, για τη σωστή απάντηση και τη λέξη Λάθος, για τη λανθασμένη.

α. Ο δείκτης διάθλασης ενός υλικού δεν εξαρτάται από την ταχύτητα του φωτός στο υλικό αυτό

β. Στα άκρα της χορδής μιας κιθάρας δημιουργούνται πάντα κοιλίες στάσιμου κύματος

γ. Το φαινόμενο του συντονισμού παρατηρείται μόνο σε εξαναγκασμένες ταλαντώσεις

δ. Οι ακτίνες Χ έχουν μικρότερες συχνότητες από τις συχνότητες των ραδιοκυμάτων

ε. Η ροπή ζεύγους είναι ίδια ως προς οποιοδήποτε σημείο. (Μονάδες 5)

ΘΕΜΑ Β

Β1. Στην ελεύθερη επιφάνεια ενός υγρού δύο σύγχρονες πηγές αρμονικών κυμάτων εκτελούν κατακόρυφες ταλαντώσεις με συχνότητα f και δημιουργούν εγκάρσια κύματα ίδιου πλάτους Α . Ένα σημείο Σ της επιφάνειας τουυγρού ταλαντώνεται εξ αιτίας της συβολής των δύο κυμάτων με πλάτος 2Α . Αν οι δύο πηγές εκτελέσουν ταλάντωση με συχνότητα 2f και το ίδιο πλάτος Α, τότε το σημείο Σ θα α. ταλαντωθεί με πλάτος 2Α . β. ταλαντωθεί με πλάτος 4 Α γ. παραμένει ακίνητο

Να επιλέξετε τη σωστή απάντηση ( μονάδες 2 )

Να δικαιολογήσετε την επιλογή σας ( μονάδες 6 ) Μονάδες 8

Β2. Δίσκος μάζας Μ είναι στερεωμένος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, και ισορροπεί

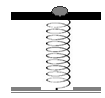( όπως στο σχήμα ) . Το άλλο άκρο του ελατηρίου είναι στερεωμένο στο έδαφος.

Στον δίσκο τοποθετούμε χωρίς αρχική ταχύτητα σώμα μάζας m.

Το σύστημα εκτελεί απλή αρμονική ταλάντωση. Η ενέργεια της ταλάντωσης είναι :

α. ½ m²g²/k β. ½ Μ²g²/k γ. ½ (m+Μ)2g² /k

Να επιλέξετε τη σωστή απάντηση ( μονάδες 2)

Να δικαιολογήσετε την επιλογή σας ( μονάδες 6) Μονάδες 8

Β3. Δύο σώματα με μάζες m₁ = 2 kg και m₂ = 3 kg κινούνται χωρίς τριβές στο ίδιο οριζόντιο 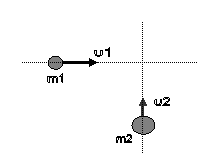επίπεδο και σε κάθετες διευθύνσεις με ταχύτητες υ ₁ = 4 m/s και υ₂ = 2 m/s ( όπως στο σχήμα ) και συγκρούονται πλαστικά.

Η κινητική ενέργεια του συσσωματώματος είναι :

α. 5 J β. 10 J γ. 20 J

Να επιλέξετε τη σωστή απάντηση ( μονάδες 2)

Να δικαιολογήσετε την επιλογή σας ( μονάδες 7) Μονάδες 9

ΘΕΜΑ Γ

Στο κύκλωμα του σχήματος δίνονται : πηγή ηλεκτρεγερτικής δύναμης Ε = 5 V μηδενικής εσωτερικής αντίστασης, πυκνωτής χωρητικότητας C = 8. 10^-6 F ,πηνίο με συντελεστή 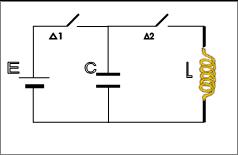αυτεπαγωγής L = 2.10^-2 H .

Αρχικά ο διακόπτης Δ₁ είναι κλειστός και ο διακόπτης Δ₂ ανοιχτός.

Γ1. Να υπολογίσετε το φορτίο του Q πυκνωτή Μονάδες 6

Ανοίγουμε τον διακόπτη Δ₁ και τη χρονική στιγμή t = 0 κλείνουμε τον διακόπτη Δ2. Το κύκλωμα LC αρχίζει να εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις .

Γ2. Να υπολογίσετε την περίοδο των ηλεκτρικών ταλαντώσεων Μονάδες 6

Γ3. Να γράψετε την εξίσωση σε συνάρτηση με τον χρόνο για την ένταση του ηλεκτρικού ρεύματος που διαρρέει το πηνίο. Μονάδες 6

Γ4. Να υπολογίσετε το ηλεκτρικό φορτίο του πυκνωτή τη χρονική στιγμή κατά την οποία η ενέργεια του μαγνητικού πεδίου είναι τριπλάσια απο την ενέργεια του ηλεκτρικού πεδίου στον πυκνωτή . Μονάδες 7

Θέμα Δ

Θέλουμε να μετρήσουμε πειραματικά την άγνωστη ροπή αδράνειας δίσκου μάζας m = 2 kg και ακτίνας r = 1 m .

Για το σκοπό αυτό αφήνουμε τον δίσκο να κυλίσει χωρίς ολίσθηση σε κεκλιμένο επίπεδο γωνίας φ = 30⁰ ξεκνώντας από την ηρεμία. Διαπιστώνουμε ότι ο δίσκος διανύει την απόσταση x = 2 m σε χρόνο t = 1 s .

Δ1. Να υπολογίσετε τη ροπή αδράνειάς του ως προς τον άξονα που διέρχεται από το κέντρο μάζας του και είναι κάθετος στο επίπεδό του. Μονάδες 7

Δ2. Από την κορυφή του κεκλιμένου επιπέδου αφήνονται να κυλίσουν ταυτόχρονα δίσκος και δακτύλιος ίδιας μάζας Μ και ίδιας ακτίνας R. Η ροπή αδράνειας του δίσκου είναι Ι₁ = ½MR ² και του δακτυλίου Ι₂ = MR² ως προς τους άξονες που διέρχονται από τα κέντρα μάζας του και είναι κάθετοι στα επίπεδά τους. Να υπολογίσετε ποιο από τα σώματα κινείται με τη μεγαλύτερη επιτάχυνση. Μονάδες 4

Συνδέουμε με κατάλληλο τρόπο τα κέντρα μάζας των δύο στερεών, όπως φαίνεται και στο σχήμα, με ράβδο αμελητέας μάζας, η οποία δεν εμποδίζει την περιστροφή τους και δεν ασκεί τριβές. Το σύστημα κυλίεται στο κεκλιμένο επίπεδο χωρίς να ολισθαίνει

Δ3. Να υπολογίσετε τον λόγο των κινητικών ενεργειών Κ₁/Κ₂, όπου Κ₁ η κινητική ενέργεια του δίσκου και Κ₂ η κινητική ενέργεια του δακτυλίου. Μονάδες 6

Δ4. Αν η μάζα κάθε στερεού είναι Μ = 1,4 kg, να υπολογίσετε τις δυνάμεις που ασκεί η ράβδος σε κάθε σώμα.

Μεταφέρετε το σχήμα στο τετράδιό σας και σχεδιάστε τις πιο πάνω δυνάμεις.

Να μην χρησιμοποιήσετε το χαρτί μιλιμετρέ που βρίσκεται στο τέλος του τετραδίου

Δίνεται : g = 10 m/s² , ημ 30^ο = ½ Μονάδες 8