ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ΄ΤΑΞΗΣ

ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΛΑΟ Γ΄ ΤΑΞΗΣ ΕΠΑΛ ( ΟΜΑΔΑ Β΄)

ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ

Τα πρώτα σχόλια

Θέμα Α.

Διαβάζουμε :

Α4 . Μία ηχητική πηγή πλησιάζει με σταθερή ταχύτητα προς έναν ακίνητο παρατηρητή και εκπέμπει ήχο συχνότητας f_s

και μήκους κύματος λ. Τότε ο παρατηρητής αντιλαμβάνεται τον ήχο α. με συχνότητα μικρότερη της f_s .

β. με συχνότητα ίση με την f_s γ. με μήκος κύματος μικρότερο του λ δ. με μήκος κύματος ίσο με λ

Σχολιάζουμε:

Στις φράσεις «εκπέμπει ήχο μήκους κύματος λ» και «αντιλαμβάνεται ήχο με κάποιο μήκος κύματος»

υπάρχει κάποιο μικρό εννοιολογικό πρόβλημα το οποίο ωστόσο εκτιμώ ότι

δεν θα δημιουργήσει προβλήματα στη βαθμολόγηση των γραπτών.

Το εννοιολογικό πρόβλημα σχετίζεται με ερωτήματα του τύπου «τι ακριβώς σημαίνει μήκος κύματος ήχου ;»

Τα διατυπώνω όσο πιο διακριτικά γίνεται:

Το μήκος κύματος ενός ήχου είναι ποσότητα η οποία νοηματοδοτείται μέσα από τη μέτρησή της από έναν παρατηρητη ;

Το μήκος κύματος ενός ήχου είναι εξ ορισμού η απόσταση στην οποία διαδίδεται η διαταραχή σε χρόνο μιας περιόδου ;

Είναι η απόσταση της ηχητικής πηγής από το μέτωπο μέγιστης διαταραχής (το δημιουργούμενο από εκπομπή t = 0) τη χρονική στιγμή t = T;

Το μήκος κύματος ενός ήχου είναι η απόσταση δύο διαδοχικών μετώπων ( μέγιστης διαταραχής ) κατά τη διεύθυνση

μιας κυματικής ακτίνας διάδοσης ;

Προτείνω να δεχθούμε ότι η φράση ήχος μήκους κύματος λ παραπέμπει κυρίως στο « σε πόση απόσταση ταξίδεψε ο ήχος – ως προς

κάποιο σύστημα αναφοράς - σε χρόνο μιας περιόδου»

ενώ η φράση αντιλαμβάνεται τον ήχο με κάποιο μήκος κύματος να θεωρηθεί – με κάποιο ζόρι ίσως –

ως το μήκος κύματος ήχου από κινούμενη πηγή το οποίο μετρά ο ακίνητος ως προς το σύστημα αναφοράς παρατηρητής-ερευνητής,

την απόσταση δηλαδή δύο διαδοχικών μετώπων ( μέγιστης διαταραχής ) κατά τη διεύθυνση μιας κυματικής ακτίνας διάδοσης

Διότι, ενώ τη μεταβολή της συχνότητας την ΑΝΤΙΛΑΜΒΑΝΕΤΑΙ με το αυτί – ως ύψος του ήχου –

δεν συμβαίνει το ίδιο με το μήκος κύματος. Στην προκειμένη δηλαδή περίπτωση ο παρατηρητής είναι

σκεπτόμενος ερευνητής και όχι ΑΚΡΟΑΤΗΣ όπως συμβαίνει στο ζήτημα της συχνότητας .

Αυτή είναι η άποψή μου, αλλά δέχομαι και αντίλογο.

http://users.sch.gr/kassetas/zzzDoppler1.htm

http://users.sch.gr/kassetas/zzzDoppler2.htm

ΘΕΜΑ Β.

Β1. Δύο όμοια ιδανικά ελατήρια κρέμονται από δύο ακλόνητα σημεία. Στα κάτω άκρα των ελατηρίων

δένονται σώματα Σ₁ μάζας m₁ και Σ₂ μάζας m₂. Κάτω από το σώμα Σ₁ δένουμε

μέσω αβαρούς νήματος άλλο σώμα μάζας m₂ , ενώ κάτω από το Σ₂, σώμα μάζας m₁ (m₁ ≠ m₂), όπως φαίνεται

στο σχήμα. Αρχικά τα σώματα είναι ακίνητα. Κάποια στιγμή κόβουμε τα νήματα και τα σώματα Σ₁ και Σ₂

αρχίζουν να ταλαντώνονται . Αν η ενέργεια της ταλάντωσης του Σ₁ είναι Ε₁ και του Σ₂ είναι Ε₂ , τότε :

α. Ε₁/Ε₂ = m₂/m₁ β. Ε₁/Ε₂ = m₂²/m₁² γ. Ε₁/Ε₂ = 1

Να επιλέξετε τη σωστή απάντηση ( Μονάδες 2 ) Να δικαιολογήσετε την επιλογή σας ( Μονάδες 6 )

Σχολιάζουμε 1:

Οι δύο μονάδες που δίνονται για την επιλογή της σωστής απάντησης, αναρωτιέσαι γιατί δίνονται.

Το να επιλέξει την Ε₁/Ε₂ = m₂²/m₁² ανάμεσα σε τρεις απαντήσεις χωρίς κανένα έλλογο στοιχείο δεν σημαίνει τίποτα

και αυτό ισχύει και για τις αντίστοιχες «2 μονάδες» στα θέμα Β2 και Β3

Αντίθετα αυτό που πρέπει να αξιολογηθεί είναι οι γνώσεις του και οι δεξιότητές του στην προσπάθεια να «δικαιολογήσει»

την επιλογή.

Σχολιάζουμε 2:

Για να καταλήξει σε μία τεκμηριωμένη «δικαιολόγηση» απαιτείται από τον εξεταζομενο :

Να γνωρίζει ότι η ενέργεια μιας αρμονικής ταλάντωσης είναι ίση με ½ DA² , όπου Α το πλάτος και D η σταθερά επαναφοράς

Να γνωρίζει ότι σε αρμονικό ταλαντωτή στο άκρο ελατηρίου η τιμή της D είναι ίση με τη σταθερά k του ελατηρίου

Να μπορεί να διακρίνει ότι το πλάτος μιας αρμονικής ταλάντωσης είναι ίσο με την απόσταση από τη θέση

στην οποία έχει μηδενική ταχύτητα μέχρι τη θέση στην οποία ισορροπούν οι δυνάμεις

Να γνωρίζει και να μπορεί να εφαρμόζει τον νόμο του Hooke

Να είναι σε θέση να εφαρμόζει την εξίσωση ισορροπίας υλικού σημείου σε τέσσερεις διαφορετικές περιπτώσεις

Να χειρίζεται τον αλγεβρικό λογισμό

Σχολιάζουμε 3:

Δεν είναι καθόλου λίγες οι απαιτούμενες γνώσεις και δεξιότητες για ΘΕΜΑ Β.

Β2. Ηχητική πηγή εκπέμπει ήχο σταθερής συχνοτητας f. Mε μια δεύτερη ηχητική πηγή δημιουργούμε ταυτόχρονα ήχο

τη συχνότητα του οποίου μεταβάλλουμε. Σε αυτήν τη διαδικασία δημιουργούνται διακροτήματα ίδιας συχνότητας

για δύο διαφορετικές συχνότητες f₁ και f₂ της δεύτερης πηγής. Η τιμή της f είναι

α. (f₁ + f₂ )/2 β. f₁f₂ /(f₁ +f₂ ) γ. (f₁ -f₂ )/2

Να επιλέξετε τη σωστή απάντηση (μονάδες 2). Να δικαιολογήσετε την επιλογή σας ( μονάδες 6 )

Σχολιάζουμε 1

Για να επιλέξει τη σωστή απάντηση δεν απαιτείται τίποτα εκτός από τη βοήθεια της θεάς Τύχης

Για να καταλήξει όμως σε μία έλλογη δικαιολόγηση απαιτείται από τον εξεταζομενο :

α. Να κατανοήσει τι ακριβώς συμβαίνει, διαβάζοντας το κείμενο. ( Εγώ και όχι μόνο χρειάστηκα κάποιο χρόνο ) .

Να κατανοήσεί σε τι ακριβώς αναφέρεται καθένα από τα τρία σύμβολα f, f₁, f₂ .

β. Να γνωρίζει ότι η συχνότητα ενός διακροτήματος είναι ίση με την απόλυτη τιμή της διαφοράς των συχνοτήτων.

γ. Να εισάγει ένα σύξμβολο ( ας υποθέσουμε το f_δ ) για τη συχνότητα του διακροτήματος

δ. Είτε στο ότι μπορεί να ανταποκριθεί στον μαθηματικό χειρισμό της f_δ = | f₁ -f₂ |

είτε στο ότι έχει κατανοήσει το τι συμβαίνει –και χωρίς να καταφύγει στη συγκεκριμένη σχέση με την απόλυτη τιμή –

μπορεί και προτείνει μία λύση του τύπου:

Εάν f₁ > f₂ , για το ένα διακρότημα η συχνότητα είναι f₁- f και για το άλλο η συχνότητα είναι f -f₂

Εφόσον οι δύο συχνότητες είναι ίσες f₁- f = f -f₂ άρα f = f₁ + f₂ )/2 .

Σε παρόμοιο συμπέρασμα καταλήγω εάν f₂ > f₁ οπότε f₂- f = f -f₁ άρα f = f₁ + f₂ )/2

Σχολιάζουμε 2

Από τη σκοπιά των γνώσεών του στη Φυσική, αξιολογείται μόνο στο εάν γνωρίζει τη σχέση ανάμεσα

στη συχνότητα ενός διακροτήματος και στις δύο συχνότητες των κυμάτων που το δημιούργησαν f_δ = |f₁ -f₂ | .

Άλλοι αξιολογούνται στο ζήτημα των αλγεβρικών τους δεξιοτήτων και άλλοι στο κατά πόσον έχουν κατανοήσει την όλη κατάσταση

και μπορούν να παρουσιάσουν μία λύση όπως αυτή που προτείναμε

Σχολιάζουμε 3

Η γλωσσική διατύπωση χωρίς να έχει κάποιο καταφέρνει να είναι

ο ΔΥΣΚΟΛΟΤΕΡΟΣ τρόπος για να περιγραφεί αυτό που περιγράφεται

Προτείνουμε εναλλακτικά ( αν και μπορούν να προταθούν και άλλες διατυπώσεις που να σου δίνουν να καταλάβεις αμέσως)

Β2. Ηχητική πηγή Α εκπέμπει ήχο σταθερής συχνοτητας f. Με την ηχητική πηγή Β δημιουργούμε ήχο τη συχνότητα

του οποίου μπορούμε και μεταβάλλουμε. Ενεργοποιούμε και τις δύο ηχητικές πηγές ταυτόχρονα

και διαπιστώνεται πως όταν η συχνότητα της Β γίνεται f₁ δημιουργείται διακρότημα συχνότητας f_δ.

Διαπιστώνεται στη συνέχεια πως όταν η συχνότητα της Β γίνεται f₂ δημιουργείται και πάλι διακρότημα

ίσης συχνότητας ( f_δ) με το προηγούμενο . Η τιμή της f είναι :

Β3. Δύο σώματα, το Α με μάζα m₁ και το Β με μάζα m₂ , είναι διαρκώς σε επαφή

και κινούνται σε λείο οριζόντιο επίπεδο με την ίδια ταχύτητα υ.

Τα σώματα συγκρούονται κεντρικά με σώμα Γ μάζας 4 m₁

το οποίο αρχικά είναι ακίνητο. Μετά την κρούση το Α σταματά ενώ το Β κολλάει στο Γ

και το συσσωμάτωμα κινείται με ταχύτητα υ/3 .

Τότε θα ισχύει : α. m₁/m₂ = 2 β. m₁/m₂ = ½ γ. m₁/m₂ = 1

Να επιλέξετε τη σωστή απάντηση (μονάδες 2). Να δικαιολογήσετε την επιλογή σας ( μονάδες 7 )

Σχολιάζουμε 1

Για να επιλέξει τη σωστή απάντηση δεν απαιτείται τίποτα εκτός από τη βοήθεια της «θεάς».

Για να καταλήξει όμως σε μία έλλογη δικαιολόγηση απαιτείται από τον εξεταζόμενο τα παρακάτω με βάση και τα οποία αξιολογείται:

Να μπορεί να επιλέγει – για το συγκεκριμένο φαινόμενο – από το σύνολο των νομων την Αρχή της διατήρησης της ορμής

Να γνωρίζει και να μπορεί να χειρίζεται τις έννοιες «ορμή σώματος σε μεταφορική κίνηση» και « ορμή συστήματος σωμάτων»

Να μπορεί να εφαρμόζει την Αρχή της διατήρησης της ορμής για το σύστημα των δύο σωμάτων

Να χειρίζεται σωστά την αλγεβρική σχέση m₁υ + 0 = ( m₂ + 4m₁) υ/3 + 0

Σχολιάζουμε 2

Στη φράση « με την ίδια ταχύτητα υ» το σύμβολο υ σημαίνει ίσως το μέτρο της ταχύτητας, ίσως και την αλγεβρική της τιμή.

Μια πανάρχαια αμαρτία των Προγραμμάτων Σπουδών και των αντίστοιχων σχολικών εγχειριδίων είναι ότι

ουσιαστικά αδιαφόρησαν για το ζήτημα. Στην εξίσωαη λόγου χάρη υ = αωημωt για μία αρμονική ταλάντωση το υ αναφέρεται

και πάλι ωςταχύτητα ενώ πρόκεται για αλγεβρική τιμή ως προς συγκεκριμένο άξονα

Σχολιάζουμε 3. Η όλη διατύπωση πάντως κάνει το θέμα Β3 άμεσα κατανοητό

ΘΕΜΑ Γ.

Στην επιφάνεια ενός υγρού που ηρεμεί, βρίσκονται δύο σύγχρονες σημειακές πηγές Π₁ και Π₂, που δημιουργούν

στην επιφάνεια του υγρού εγκάρσια επιφανειακά κύματα ίσου πλάτους. Οι πηγές αρχίζουν να ταλαντώνονται

τη χρονική στιγμή t₀ = 0 ξεκινώντας από τη θέση ισορροπίας τους και κινούμενες προς την ίδια κατεύθυνση,

την οποία θεωρούμε θετική . Η χρονική εξίσωση της ταλάντωσης ενός σημείου Μ, που βρίσκεται

στη μεσοκάθετο του ευθύγραμμου τμήματος Π₁Π₂, μετά τη συμβολή των κυμάτων δίνεται στο SI

από τη σχέση y_M = 0,2ημ2π(5t – 10).

Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι υ = 2 m/s .

Έστω Ο το μέσο του ευθυγράμμου τμήματος Π₁Π₂ και d = 1 m η απόσταση μεταξύ των δύο πηγών.

Να βρείτε : Γ1. Την απόσταση ΜΠ₁ Μονάδες 5

Γ2. Τη διαφορά φάσης των ταλαντώσεων των σημείων Ο και Μ Μονάδες 6

Γ3. Πόσα σημεία του ευθύγραμμου τμήματος Π₁Π₂, ταλαντώνονται με μέγιστο πλάτος Μονάδες 7

Γ4. Να σχεδιάσετε τη γραφική παράσταση της απομάκρυνσης του σημείου Μ

σε συνάρτηση με τον χρονο t για 0 ≤ t ≤ 2,5 s Μονάδες 7

Διαβάζουμε :

Οι πηγές αρχίζουν να ταλαντώνονται τη χρονική στιγμή t₀ = 0 ξεκινώντας από τη θέση ισορροπίας τους

και κινούμενες προς την ίδια κατεύθυνση, την οποία θεωρούμε θετική.

Σχολιάζουμε :

Το ξεκινώντας είναι του ρήματος ξεκινώ, σε λόγια διατύπωση «εκκινώ».

Πρόκειται για εκκίνηση, όπως εκείνη του δρομέα και σημειολογικά παραπέμπει σε μηδενική αρχική ταχύτητα

η οποία είναι αδύνατον να γίνει ακαριαία μέγιστη ταχύτητα μιας ταλάντωσης.

Όταν ένας ακίνητος ταλαντωτής ΞΕΚΙΝΑΕΙ σημαίνει ότι βρίσκεται στο άκρο της ταλάντωσης.

Ένας ταλαντωτής που βρίσκεται σε θέση ευσταθούς ισορροπίας θα εκτελέσει αρμονική ταλάντωση εάν ΕΝΕΡΓΟΠΟΙΗΘΕΙ κατάλληλα.

Προτείνουμε ( αν και θα μπορούσαν να διατυπωθουν και καλύτερες προτάσεις ) :

Οι δύο πηγές ενεργοποιούνται ταυτόχρονα τη χρονική στιγμή t₀ = 0 και καθεμία εκτελεί κατακόρυφη αρμονική ταλάνωση.

Κατά τη χρονική στιγμή t₀ = 0 θεωρούμε ότι και οι δύο βρίσκονται στη θέση ισορροπίας τους κινούμενες προς την ίδια κατεύθυνση,

την οποία θεωρούμε θετική .

Διαβάζουμε τις λύσεις που προτείνονται και σχολιάζουμε :

Κεντρικό γνωστικό αντικείμενο για τη λύση της άσκησης

είναι η συνάρτηση y = 2Aσυν2π(r₁-r₂)/2λ ημ2π[t/T - (r₁+r₂)/2λ] .

Αν ένας μαθητής τη χρησιμοποιήσει, γράφοντάς την, διότι τον έχουν πείσει να την «ξέρει απέξω»

θα πάρει τον ίδιο βαθμό με έναν μαθητή ο οποίος βασιζόμενος

στη μαθηματική περιγραφή του αρμονικού κύματος,

στην αρχή της superposition - υπέρθεσης και

στο να μετατρέπει ένα άθροισμα ημιτόνων σε γινόμενο

θα καταλήξει σε αυτήν.

Και ο μαθητής που έχει αποστηθίσει τη συνάρτηση δικαιώνεται, μαζί και ο καθηγητής του σχολείου

ή ο φροντιστής που τον έπεισε να αποστηθίζει και του έχει μεταδώσει το ότι «η Φυσική είναι κάποιοι τύποι»

Γιατί εάν κρίνω από την ποιότητα των απαντήσεων στα θέματα, στις εφημερίδες και στην τηλεόραση

η επίσημη εκδοχή είναι τελικά αυτή. Να έχουν απομνημονεύσει οι μαθητές

μία συνάρτηση χωρίς να εμφανιζεται στο σχολικό βιβλίο έστω σε κάποιο πλαίσιο

Αναρωτιέται κανείς: Τι ακριβώς αξιολογούμε ως αποτέλεσμα της διδασκαλίας μας ;

Το να ξέρουν οι μαθητές απέξω ότι y = 2Aσυν2π(r₁-r₂)/2λ ημ2π[t/T - (r₁+r₂)/2λ];

Είναι άραγε αυτός ένας από τους στόχους της διδασκαλίας μας ;

Είναι άραγε αυτή μία απαντήσεις στο ερώτημα «Γιατί διδάσκουμε Φυσική;» .

Υπάρχει στο Αναλυτικό μας Πρόγραμμα ο στόχος « Να γνωρίζουν οι διδασκόμενοι τη συνάρτηση

y = 2Aσυν2π(r₁-r₂)/2λ ημ2π[t/T - (r₁+r₂)/2λ]». Και ξέρω καλά ότι δεν υπάρχει.

Αντίθετα το πνεύμα του Αναλυτικού Προγράμματος είναι «να γνωρίζει ορισμένα θεμελιακά

στοιχεία και να είναι σε θέση να τα χρησιμοποιεί ώστε να ερμηνεύει και να προβλέπει ένα φαινόμενο» όπως, στην προκειμένη περίπτωση η συμβολή των κυμάτων.

Και η συνάρτηση y = 2Aσυν2π(r₁-r₂)/2λ ημ2π[t/T - (r₁+r₂)/2λ] δεν είναι, σε καμία

περίπτωση, θεμελιακό στοιχείο της Φυσικής.

Το συγκεκριμένο ζήτημα είναι ενδεικτικό της όλο και πιο χαμηλής ποιότητας που έχει αρχίσει να κυριαρχεί

στη διδασκαλία του μαθήματος. Βασικό χαρακτηριστικό η εκφρασμένη άρνηση μεγάλου μέρους

των μαθητών στο να διδαχθούν ότιδήποτε δεν έχει άμεση σχέση με εξετάσεις και στη διαμόρφωση μιας

σκληρής πεποίθηση ότι «η Φυσική είναι κάτι τύποι, αν τους μάθεις ξέρεις Φυσική».

Μολονότι είναι κάπως σχηματοποιημένο και θέλω να αποφεύγω τις σχηματοποιήσες,

νομίζω όμως ότι η υπόθεση «διδασκαλία Φυσικής στην Τρίτη Λυκείου» έχει φθάσει στο τέλος της.

Πρέπει να ετοιμάζουμε τη διαφορετική πρόταση για το μέλλον.

Διαβάζουμε

Γ2. Τη διαφορά φάσης των ταλαντώσεων των σημείων Ο και Μ

Γ3. Πόσα σημεία του ευθύγραμμου τμήματος Π₁Π₂, ταλαντώνονται με μέγιστο πλάτος

Σχολιάζουμε και θέτουμε το ερώτημα «το γεωμετρικό σημείο έχει κινητική ενέργεια;»

Τι ακριβώς είναι «αυτό που εκτελεί ταλάντωση κατά τη συμβολή των κυμάτων;»

Η απάντηση βέβαια που δίνει η εκφώνηση είναι ότι «αυτό που εκτελεί ταλάντωση είναι ένα ΣΗΜΕΙΟ.

Και εξυπακούεται ότι λέγοντας ΣΗΜΕΙΑ ΤΟΥ ΕΥΘΥΓΡΑΜΜΟΥ ΤΜΗΜΑΤΟΣ εννοεί ΓΕΩΜΕΤΡΙΚΑ ΣΗΜΕΙΑ.

Είναι γεγονός ότι ένα γεωμετρικό σημείο – το άκρο μιας σκιάς ή το κέντρο μάζας μιας ράβδου - μπορεί να εκτελεί ταλάντωση,

μπορεί να έχει θέση, ταχύτητα ακόμα και επιτάχυνση. ΔΕΝ ΜΠΟΡΕΙ ΟΜΩΣ ΝΑ ΕΧΕΙ ΟΡΜΗ ΚΑΙ ΕΝΕΡΓΕΙΑ

και κύμα σημαίνει πριν απόλα «μεταφορά ενέργειας».

Το υποκειμενο σε ταλάντωση στην περίπτωση ενός κύματος είναι οπωσδήποτε ένα ΥΛΙΚΟ ΣΗΜΕΙΟ - μπορούμε

να το λέμε και ΣΗΜΕΙΑΚΟ ΑΝΤΙΚΕΙΜΕΝΟ - ένα «κομμάτι Σύμπαντος» με αδράνεια, με ορμή, με ενέργεια .

Διαβάζουμε

Γ2. Τη διαφορά φάσης των ταλαντώσεων των σημείων Ο και Μ

Σχολιάζουμε

Μία διαφορά φάσης θα μπορούσε, εκτός τοωνάλων, να αναφέρεται

α. σε ΈΝΑ ταλαντούμενο υλικό σημείο και σε ΔΥΟ χρονικές στιγμές ( ως διαφορά φάσης των τιμών θέσης-απομάκρυνσης )

β. Σε ΔΥΟ υλικά σημεία κάποιου κύματος και σε ΜΙΑ χρονική στιγμή ( ως διαφορά φάσης των τιμών θέσης-απομάκρυνσης )

Η συγκεκριμένη διατύπωση οδηγεί βέβαια τη σκέψη προς το δευτερο. Η συγκεκριμένη διατύπωση θα μπορούσε να είναι σαφέστερη

αποδίδοντας έμφαση στο ότι πρόκειται για ΜΙΑ χρονική στιγμή

Προτείνουμε

Τη διαφορά φάσης των ταλαντώσεων ( ή θέσεων ) δύο υλικών σημείων του μέσου τα βρίσκονται στις θέσεις Ο και Μ,

σε μια τυχαία χρονική στιγμή κατά την οποια και τα δύο υλικά σημεία έχουν ενεργοποιηθεί

Σκεφτόμαστε ότι :

Η λύση απαιτεί από τον εξεταζόμενο επάρκεια στα παρακάτω, με βάση τα οποία και αξιολογείται:

1. Να έχει εξοικειωθεί με τις έννοιες πλάτος ταλάντωσης και συχνότητα ταλάντωσης,

2. Να αναγνωρίζει τις έννοιες μήκος κύματος, ταχύτητα διάδοσης και συχνότητα κύματος καθώς και τη σχέση που συνδέει τις τιμές τους

3. Να γνωρίζει ότι η απόσταση x στην οποία διαδίδεται μία κυματική διαταραχή σχετίζεται με το αντίστοιχο χρονικό διάστημα t με τη

σχέση x = υt ή να καταλήγει λογικά στο με βάση το ότι «η τιμή της ταχύτητας 2m/s υποδηλώνει ότι σε κάθε δευτερόλεπτο

η διαταραχή διαδίδεται 2 m» και με Αριθμητικη να καταλήγει στο ζητούμενο .

4. Να έχει κατανοήσει το πώς εξελίσσεται το φαινόμενο «συμβολή κυμάτων στην επιφάνεια υγρού»

5. Να είναι σε θέση να αποδείξει ή να «ξέρει απέξω» τη συνάρτηση y = 2Aσυν2π(r₁-r₂)/2λ ημ2π[t/T - (r₁+r₂)/2λ]

6. Να έχει κατανοήσει ότι η εμφανιζόμενη στο πρόβλημα «διαφορά φάσης αναφέρεται

α. σε ΔΥΟ υλικά σημεία του ελαστικού μέσου β. σε ΜΙΑ ορισμένη χρονική στιγμή

7. Να γνωρίζει με τι είναι ίση η τιμή μιας φάσης

8. Να γνωρίζει ότι τα υλικά σημεία που εκδηλώνεται ενίσχυση της συμβολής – ταλαντώνονται με το μεγαλύτερο πλάτος- είναι εκείνα

για τα οποία η διαφορά των αποστάσεων από τις δύο πηγές είναι ακέραιο πολλαπλάσιο του μήκους κύματος

9. Να μπορεί να διακρίνει απλά χωρικά ζητήματα, όπως ότι για κάθε γεωμετρικό σημείο του τμήματος Π₁ Π₂ ισχύει r₁+r₂ = d

10. Να μπορεί να χειρίζεται αλγεβρικές εξισώσεις, ανισώσεις αλλά και τριγωνομετρικές συναρτήσεις

11. Να μπορεί να αποδίδει σε γραφική παράσταση μία συνάρτηση y = 0,2 ημ( 10πt- 20π) για ορισμένες τιμές του t

ΘΕΜΑ Δ.

Αβαρής ράβδος μήκους 3 d ( d = 1m ) μπορεί να στρέφεται γύρω από οριζόντιο άξονα, που είναι κάθετος σε αυτή

και διέρχεται από το Ο. Στο άκρο

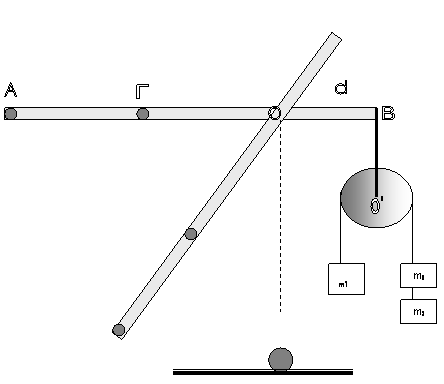
Στο άκρο Α που βρίσκεται σε αποσταση 2d από το Ο υπάρχει σημειακή μάζα m_A = 1 kg και στο σημείο Γ,

που βρίσκεται σε απόσταση d από το Ο, έχουμε επίσης σημειακή μάζα m_Γ = 6 kg. Στο άλλο άκρο της ράβδου,

στο σημείο Β, είναι αναρτημένη τροχαλία μάζας Μ = 4 kg από την οποία κρέμονται οι μάζες m₁ = 2 kg

και m₂ = m₃ = 1 kg . Η τροχαλία μπορεί να περιστρέφεται γύρω από άξονα Ο΄.

Δ1. Αποδείξτε ότι το σύστημα ισορροπεί με τη ράβδο στην οριζόντια θέση. Μονάδες 4

Κόβουμε το ϴ που συνδέει την τροχαλία με τη ράβδο στο σημείο Β.

Δ2. Βρείτε τη γωνιακή επιτάχυνση της ράβδου, όταν αυτή σχηματίζει γωνία 30^ο με την κατακόρυφο. Μονάδες 7

Όταν η σημειακή μάζα m_A φτάνει στο κατώτατο σημείο,

συγκρούεται πλαστικά με ακίνητη σημειακή μάζα m₄ = 5 kg.

Δ3. Βρείτε τη γραμμική ταχύτητα του σημείου Α αμέσως μετά την κρούση Μονάδες 6

Στην αρχική διάταξη, όταν η τροχαλία με τα σώματα είναι δεμένη στο Β, κόβουμε το νήμα που συνδέει

μεταξύ τους τα σώματα m₂ και m₃ και αντικαθιστούμε την m_A με μάζα m_.

Δ4. Πόση πρέπει να είναι η μάζα m, ώστε η ράβδος να διατηρήσει την ισορροπία της κατά τη διάρκεια

της περιστροφής της τροχαλίας. Μονάδες 8

Τα νήματα είναι αβαρή, τριβές στους άξονες δεν υπάρχουν και το νημα δεν ολισθαίνει στην τροχαλία. Δίνεται g = 10m/s2, ημ30^ο = ½ ,

Η ροπή αδράνειας της τροχαλίας ως προς άξονα που διέρχεται από το κέντρο της Ι = ½ ΜR².

Ενστάσεις σχετικά με ορισμένες διατυπώσεις

Η φράση «Στο άκρο Α που βρίσκεται σε αποσταση 2d από το Ο υπάρχει σημειακή μάζα m_A = 1 kg και στο σημείο Γ,

που βρίσκεται σε απόσταση d από το Ο, έχουμε επίσης σημειακή μάζα m_Γ = 6 kg»

δεν εκφράζει ότι και τα δύο σημειακά αντικείμενα είναι συγκολλημένα με τη ράβδο. Ούτε το «υπάρχει σημειακή μάζα» ούτε

το «έχουμε σημειακή μάζα» σημαίνουν ότι πρόκειται για αντικείμενα συγκολλημένα στη ράβδο

Δύο σημειακά αντικείμενα είναι συγκολλημένα με τη ράβδο. Το ένα μάζας m_A = 1 kg βρίσκεται στο άκρο Α σε απόσταση 2d από το Ο

ενώ το άλλο μάζας m_Γ = 6 kg σε απόσταση d από το Ο

Διαβάζουμε : τροχαλία μάζας Μ = 4 kg από την οποία κρέμονται οι μάζες m₁ = 2 kg και m₂ = m₃ = 1 kg

Σχολιάζουμε

Η φράση συρρικνώνει τη γλωσσική περιγραφή - τα αντικείμενα m₁ και m₂ συνδέονται με νήμα που περιβάλλει τηντροχαλία –

και την αναθέτει στο σχήμα

Προτείνουμε :

τα αντικείμενα μαζών m₁ = 2 kg και m₂ = 1 kg συνδέονται με νήμα που περιβάλλει την τροχαλία

ενώ ένα κατακόρυφο νήμα συνδέει το αντικείμενο μάζας m₂ με αντικείμενο μάζας m₃ = 1 kg

Διαβάζουμε :

Κόβουμε το ϴ που συνδέει την τροχαλία με τη ράβδο στο σημείο Β

Σχολιάζουμε

Με τη φράση αυτή γίνεται αναφορά σε κάποιο αντικείμενο ϴ για τη μάζα του οποίου δεν αναφέρεται τίποτα. Το σχήμα

το παρουσιάζει ιδιαίτερα παχύ για να είναι νήμα αλλά «η άνεση με την οποία το κόβουμε» οδηγεί τη σκέψη

στο ότι πρόκειται για κάποιο νήμα παχύτερο από τα άλλα νήματα, άρα αντικείμενο αμελητέας μάζας.

Προτείνουμε :

Κόβουμε το νήμα ϴ που συνδέει την τροχαλία με τη ράβδο στο σημείο Β

Διαβάζουμε :

Όταν η σημειακή μάζα m_A φτάνει στο κατώτατο σημείο, συγκρούεται πλαστικά με ακίνητη σημειακή μάζα»

Σχολιάζουμε :

Με τη φράση αυτή τα πράγματα είναι πιο σοβαρά.

Η κρούση συνιστά φαινόμενο κατά το οποίο συγκρούονται δύο συγκεκριμένα αντικείμενα. Καθένα από αυτά τα δύο αντικείμενα έχει

συγκεκριμένα χαρακτηριστικά αδράνειας και συγκεκριμένη κινητική κατάσταση.

Στην προκειμένη περίπτωση τα δύο αντικείμενα είναι

α. η ράβδος με τα συγκολλημένα σημειακά αντικείμενα ως ένα σώμα κα β. το σημειακό αντικείμενο μάζας m₄ .

Ή διατύπωση όταν η σημειακή μάζα m_A φτάνει στο κατώτατο σημείο, συγκρούεται πλαστικά με ακίνητη σημειακή μάζα m₄ εκτός του ότι είναι ατυχέστατη γλωσσικά δημιουργεί και παρανόηση ότι πρόκειται για κρούση

δύο σημειακών αντικειμένων και παραπλανεί, οδηγώντας τη σκέψη του εξεταζόμενου στο να θεωρήσει ότι το σύστημα των συγκρουομένων σωμάτων είναι το « μάζα m_A και μάζα m₄ » και «δικαιολογημένα» να καταφύγει στη διατήρηση της ορμής του συστήματος « μάζα m_A και μάζα m₄ »

Προτείνουμε :

Όταν η ράβδος γίνεται κατακόρυφη, συγκρούεται πλαστικά με το ακίνητο σημειακό αντικείμενο μάζας m₄ = 5 kg

Διαβάζουμε :

Δίνεται g = 10m/s2, ημ30ο = ½ , ροπή αδράνειας της τροχαλίας ως προς άξονα που διέρχεται από το κέντρο της Ι = ½ ΜR².

Προτείνουμε :

Δίνονται η τιμή της βαρυτικής επιτάχυνσης g = 10m/s², ότι ημ30ο = ½ και η σχέση Ι = ½ΜR² για τη ροπή αδράνειας Ι της τροχαλίας

– R η ακτίνα της - ως προς οριζόντιο άξονα που διέρχεται από το κέντρο της.

Σκεφτόμαστε ότι :

Η λύση απαιτεί από τον εξεταζόμενο επάρκεια στα παρακάτω, με βάση τα οποία και αξιολογείται:

1. Να έχει εξοικειωθεί με τις έννοιες δύναμη και ροπή δύναμης ως προς σημείο .

2. Να μπορεί να χειρίζεται τις γεωμετρικές έννοιες «απόσταση σημείου» από «ευθεία και απόσταση σημείου από επίπεδο»

3. Να μπορεί να υπολογίζει την αλγεβρική ποσότητα « αλγεβρικό άθροισμα των ροπών»

ή «αλγεβρική τιμής της ολικής ροπής - ενός συνόλου δυνάμεων

4. Να γνωρίζει τις συνθήκες ισορροπίας ενός στερεού στρεπτού περί άξονα

και να μπορεί να εφαρμόζει και να χειρίζεται αλγεβρικά τη σχέση «ολική ροπή ως προς συγκεκριμένο σημείο = μηδέν »

5. Να έχει εξοικειωθεί με τις έννοιες ταχύτητα υλικού σημείου και σώματος σε μεταφορική κίνηση

και γωνιακή ταχύτητα υλικού σημείου και στρρφομένου στερεού

6. Να έχει εξοικειωθεί με τις έννοιες γωνιακή επιτάχυνση υλικού σημείου και στρεφομένου στερεού και ροπή αδράνειας ως προς άξονα,

7. Να μπορεί να υπολογίζει την τιμή της ροπής αδράνειας μιας διάταξης

ως άθροισμα των ροπών αδράνειας των επι μέρους τμημάτων της

8. Να είναι σε θέση να εφαρμόζει τον θεμελιώδη νόμο για τη στροφική κίνηση σε συγκεκριμένη χρονική στιγμή

κατά τη στροφική κίνηση μιας ράβδου και να διαχειρίζεται την προκύπτουσα αλγεβρική σχέση

9. Να γνωρίζει και να χειρίζεται τις έννοιες κινητική ενέργεια στρεφομένου στερεού και

βαρυτική δυναμική ενέργεια ενός συστήματος ως προς οριζόντια επιφάνεια αναφοράς

10. Να είναι σε θέση, κατά την κινηση ενός σώματος σε διατηρητικό περιβάλλον, να εφαρμόζει τη Διατήρηση της ενέργειας ενός συστήματος (ή το θεώρημα έργου – ενέργειας) και να διαχειρίζεται την αλγεβρική εξίσωση που προκύπτει

11. Να έχει εξοικειωθεί με τις έννοιες «στροφορμή υλικού σημείου», «στροφορμή στρεφομένου στερεού και «στροφορμή συστήματος»

και να γνωρίζει ότι καθεμία αναφέρεται σε ορισμένο γεωμετρικό σημείο

12. Να είναι σε θέση, προκειμένου να ερευνήσει ένα φαινόμενο κρούσης και να αναζητήσει συσχετισμούς, να εφαρμόζει

τη Αρχή της διατήρηση της στροφορμής του συστήματος, ως προς ορισμένο σημείο ως προς το οποίο η ολική ροπή είναι μηδέν,

και να διαχειρίζεται την προκύπτουσα αλγεβρική σχέση

13. Να έχει εξοικειωθεί με τις έννοιες επιτάχυνση υλικού σημείου ( ή σώματος σε μεταφορικη κίνηση ) και επιτρόχια ( εφαπτομενική) επιτάχυνση υλικού σημείου σε κυκλική κίνηση.

14. Να γνωρίζει ότι η επιτρόχια επιτάχυνση των σημείων της περιφέρειας ενός τροχού σχετίζεται με τη γωνιακή επιτάχυνση του τροχού με την α = α_γR , όπου R η ακτίνα του τροχού

15. Να είναι σε θέση να εφαρμόζει τον δεύτερο νευτωνικό νόμο της κίνησης σε ένα υλικό σημείο κάθε φορά

και να διαχειρίζεται τις προκύπτουσες αλγεβρικές σχέσεις.

16. Να είναι σε θέση να εφαρμόζει τον θεμελιώδη νόμο για τη στροφική κίνηση

κατά τη στροφική κίνηση μιας τροχαλίας και να διαχειρίζεται την προκύπτουσα αλγεβρική σχέση

17. Να γνωρίζει ότι εφόσον ένα νήμα έχει αμελητέα μάζα, η δύναμη που ασκείται στο νήμα από το σώμα που βρίσκεται

στο ένα άκρο του είναι ίση με τη δύναμη που ασκεί το νήμα στο σώμα που βρίσκεται στο άλλο άκρο

18. Να μπορεί να περιγράφει τη δύναμη που ασκεί ένα νήμα σε τροχαλία με ορισμένη μάζα

19. Να διαθέτει δεξιότητες στο να λύνει ένα συστήμα εξισώσεων

Οι απαιτήσεις είναι πάρα πολλές και για να ανταποκριθεί ο μαθητής ή η μαθήτρια οι οποίοι έχουν τις σχετικές δεξιότητες απαιτείται χρόνος και ο χρόνος δεν φαίνεται να είναι αρκετός

Το βασικό στοιχείο των φετεινών θεμάτων είναι ο ΧΡΟΝΟΣ που απαιτήθηκε για να αντιμετωπιστούν ιδιαίτερα τα δύο τελευταία θέματα. Δημιουργήθηκε με άλλα λόγια ένα θέμα «ποσότητας», ενώ η «ποιότητα»διατηρήθηκε σε κάποιο επίπεδο σχετικά αξιοπρεπές, μαζί με τις ενστάσεις που υποβάλλαμε .

Θα επανέλθω και για να συμπληρώσω αλλά και για να διορθώσω κάποια σφάλματα που ενδεχομένως έκανα, δεδομένης της βίασης και της βιάσης

Ανδρέας Ιωάννου Κασσέτας

Σάββατο 21 Μαίου ώρα 13.50