Ανδρέας Ιωάννου Κασσέτας

Η ΑΡΧΗ ΤΗΣ ΑΝΕΞΑΡΤΗΣΙΑΣ

των ταυτόχρονων κινήσεων

1. Galileo Galilei και μια «Αλήθεια» αναντίρρητη

Μια από τις αναντίρρητες «αλήθειες», που επί αιώνες κυριαρχούσε χωρίς ουσιαστικό αντίπαλο ήταν

η ιδέα ότι «η Γη είναι το ακίνητο κέντρο του Σύμπαντος.

Είχε αποκρυσταλλωθεί στις συνειδήσειςτων ανθρώπων ως ένα είδος ΑΥΤΟΝΟΗΤΟΥ,

όχι μόνο επειδή ήταν μια αλήθεια της Αγίας Γραφής. Βασιζόταν και σε δύο «λογικά» επιχειρήματα- ερωτήματα στα οποία δεν μπορούσε να δοθεί ικανοποιητική απάντηση ακόμα κι όταν ο Κοπέρνικος πρότεινε το ηλιοκεντρικό μοντέλο . Και τα δύο οδηγούσαν «λογικά» στο «είναι αδύνατον να κινείται

ο πλανήτης μας».

Το πρώτο ήταν το «αδιανότητο» να κινείται η Γη με τόσο μεγάλη ταχύτητα και οι άνθρωποι να διατηρούνται και να κοιμούνται ήσυχοι πάνω της.

Το δεύτερο ήταν το χωρίς απάντηση ερώτημα « εάν η Γη στρέφεται, γιατί μια πέτρα που πέφτει από την κορυφή ενός κατακόρυφου πύργου δεν πέφτει μακριά από τον τοίχο ή πάνω στον τοίχο του πύργου ; »

Ευρισκόμενος από καιρό στο επίκεντρο της σύγκρουσης με τους αριστοτελικούς φυσικούς, οι οποίοι υποστήριζαν το γεωκεντρικό μοντέλο του Πτολεμαίου, ο Γαλιλαίος θα προτείνει δύο βασικές αρχές

( principia ) για τη Νέα Επιστήμη της κίνησης. Το βασικό του κίνητρο ήταν η στήριξη του

ηλιοκεντρικού μοντέλου του Κοπέρνικου.

2. Η αρχή της σχετικότητας

Η πρώτη από τις δύο αρχές είναι η κλασική, όπως χαρακτηρίστηκε αργότερα, αρχή της σχετικότητας. Αναφέρεται στη λεγόμενη ΣΧΕΤΙΚΗ ΚΙΝΗΣΗ, στο «πώς βλέπει την κίνηση ενός αντικειμένου ένας κινούμενος παρατηρητής».

Με την αρχή αυτή, ο Γαλιλαίος, θέλει, εκτός των άλλων, να δείξει ότι «είναι δυνατόν στους κατοίκους της Γης να διατηρούνται σε σχετική ισορροπία πάνω στη Γη παρά τη μεγάλη ταχύτητα της Γης » και κατά συνέπεια ότι το ηλιοκεντρικό μοντέλο είναι συμβατό με τα γεγονότα .

Η γαλιλαιική αρχή της σχετικότητας, εμπλουτισμένη από τις νευτωνικές θεωρήσεις για «απόλυτο χρόνο» ότι ένα, δηλαδή χρονικό διάστημα έχει τιμή ανεξάρτητη από την κίνηση του παρατηρητή και για απόλυτο χώρο, ότι δηλαδή η απόσταση δύο σημείων είναι επίσης ανεξάρτητη από την κίνηση του παρατηρητή , θεωρήθηκε επί αιώνες περίπου προφανής, ελάχιστοι στοχαστές ασχοληθηκαν με το ζήτημα , μέχρι τις αρχές του 20^ου αιώνα, οποτε ο Αϊνστάιν εστίασε σε αυτήν, δίνοντας στη μαθηματική της περιγραφή το όνομα «Μετασχηματισμοί του Γαλιλαίου» και στη συνέχεια, αμφισβητώντας τις νευτωνικές παραδοχές για απόλυτο χρόνο και χώρο, έκανε μια πρόταση διαφορετική.

Η πρωταρχική ΙΔΕΑ είναι του Γαλιλαίου, αλλά η διατύπωση που σφράγισε

τα όσα ακολουθησαν στη Μηχανική έγινε από τον Isaac Newton .

PRINCIPIA MATHEMATICA . CORROLLARΙUM V. Corporum dato spatio inclusorum iidem sunt motus inter se,

sive spatium illud quiescat, sive moveatur idem uniformiter in directum absque motu circulari.

CORROLLARY V. The motion of bodies included in a given space are the same among themselves ,

whether the space is at rest, or moves uniformly forwards in a right line whitout any circular motion .

Πόρισμα 5. Η σχετική κίνηση σωμάτων σε ένα δεδομένο χώρο είναι ίδια,

είτε ο χώρος ακινητεί είτε κινείται ομαλά σε ευθεία γραμμή χωρίς οποιαδηποτε κυκλική κίνηση

Η πρόταση αυτή θα εξελιχθεί στην λεγόμενη νευτωνική αρχή της σχετικότητας

Οι νόμοι της Μηχανικής είναι ίδιοι για όλα τα αδρανειακά συστήματα αναφοράς.

Στην αυγή του 20^ου αιώνα, ο Albert Einstein θα την επεκτείνει για όλη τη Φυσική.

Οι νόμοι της Φυσικής είναι ίδιοι για όλα τα αδρανειακά συστήματα αναφοράς.

Αρχή της σχετικότητας, σύμφωνα με τον Einstein

O ίδιος ο Einstein γράφει « οι νόμοι της Ηλεκτροδυναμικής και της Οπτικής

ισχύουν για όλα τα συστήματα αναφοράς, στα οποία ισχύουν οι νόμοι της Μηχανικής»

3. Η αρχή της ανεξαρτησίας

των ταυτόχρονων κινήσεων.

Από τον Galileo στον Newton.

α. Ο Γαλιλαίος

Η δεύτερη αρχή που προτείνει ο Γαλιλαίος αναφέρεται στη ΣΥΝΘΕΣΗ ΚΙΝΗΣΕΩΝ ενός σώματος . Στη γλωσσική παράδοση των Ιταλών χαρακτηρίζεται

Il Principio di composizione ( o di indipendenza ) dei moti simultanei, di Galileo

- Η αρχή της σύνθεσης ( ή της ανεξαρτησίας ) των ταυτόχρονων κινήσεων.

Σύμφωνα με αυτήν

« Σε μια κίνηση, την οποία η σκέψη μας μπορεί να θεωρήσει σύνθετη,

οι συνιστώσες κινήσεις λαμβάνουν χώρα ανεξάρτητα η μία από την άλλη». Η εξέλιξη της μιας κίνησης δεν αλλοιώνεται από την ύπαρξη της ταυτόχρονης άλλης κίνησης ».

Η αρχή αυτή θεωρείται μεγάλης σημασίας για την οικοδόμηση της Νέας Επιστήμης δεδομένου ότι ο Γαλιλαίος, βασιζόμενος σε αυτήν, θα απορρίψει πειστικά το άλλο ισχυρό επιχείρημα των αριστοτελικών και θα δώσει απάντηση στο μέχρι τότε αναπάντητο ερώτημα « εάν η Γη κινείται, γιατί μια πέτρα που πέφτει από την κορυφή ενός κατακόρυφου πύργου δεν πέφτει μακριά από τον τοίχο ή πάνω στον τοίχο του πύργου ; »

Η εμπειρία ενίσχυε την ιδέα. Αφήνοντας ένα βαρύ αντικείμενο από την κορυφή ενός καταρτιού κινούμενου ιστιοφόρου, το αντικείμενο έφθανε ακριβώς στη βάση του καταρτιού. Μία ερμηνεία του εμπειρικού δεδομένου ότι το αντικείμενο, όταν αφηνόταν ελεύθερο από ψηλά, «είχε» και την οριζόντια ταχύτητα του σκάφους και στη συνέχεια η κίνησή του προς τα κάτω του γινόνταν ΑΝΕΞΑΡΤΗΤΑ από την ταχύτητα αυτή .

Έφθανε στη βάση στον ίδιο χρόνο που θα έφθανε αν δεν είχε την οριζόντια ταχύτητα .

Ο ίδιος ο Γαλιλαίος, βασιζόμενος

στην αρχή αυτή,

έλυσε το άλυτο μέχρι τότε

πρόβλημα

της κίνησης των βλημάτων.

DISCORSI E DIMOSTRAZIONI MATEMATICHE INTORNO A DUE NUOVE SCIENZE
Διάλογοι και μαθηματικές αποδείξεις γύρω από δύο νέες επιστήμες

TEOREMA I PROPOSIZIONE I

Un proietto, mentre si muove di moto composto orizzontale equabilee di moto deorsum naturalmente accelerato, descrive nel suo movimento una linea semiparabola

ΘΕΩΡΗΜΑ Ι ΠΡΟΤΑΣΗ Ι

Ένα βλήμα ενώ κινείται με κίνηση συντιθέμενη από οριζόντια ομαλή κίνηση και από κίνηση deorsum (;) φυσικά επιταχυνομενη, διαγράφει κατά την κίνησή του μια γραμμή ημιπαραβολική

β. Γαλιλαίος και Καρτέσιος .

Το 1637, ο Καρτέσιος – Descartes, πεπεισμένος ότι τα φαινόμενα θα μπορούσαν να περιγραφούν

στη γλώσσα ΜΑΘΗΜΑΤΙΚΩΝ, στο Discourse de la Methode - Περί Μεθόδου Λόγος- καταθέτει την ιδέα ότι η ΘΕΣΗ ενός γεωμετρικού σημείου θα μπορούσε να περιγραφεί με τρεις αριθμούς,

τις καρτεσιανές συντεταγμένες όπως λέμε σήμερα.

Ο συνδυασμός της εντυπωσιακής πρότασης του Καρτέσιου για κάθετους άξονες , με την ιδέα του Γαλιλαίου για ανεξαρτησία των ταυτόχρονων κινήσεων, στον πυρήνα της οποίας υπάρχει το « η ισότητα των χρόνων στους οποίους θα έκανε καθεμιά από τις άλλες κινήσεις», οδήγησε και στην επόμενη ιδέα ότι «οι δύο ανεξάρτητες κινήσεις του υλικού σημείου αντιστοιχούν στις κινήσεις των γεωμετρικών σημείων, τα οποία είναι οι προβολές των θέσεων του υλικού σημείου στους άξονες», οδήγησε με άλλα λόγια στην αναλυτική περιγραφή της επίπεδης κίνησης με σύστημα καθέτων αξόνων x , y και στις δύο χρονικές συναρτήσεις, οι οποίες στην περίπτωση μιας οριζόντιας βολής είναι η

x = υ₀t και y = ½αt², με το t να είναι ΚΟΙΝΟ.

Οι φυσικοί του μέλλοντος μπορούσαν να περιγράφουν την κίνηση με τον αναλυτικό τρόπο των δύο συναρτήσεων και ισοδύναμα να προβλέπουν τη θέση του κινητού στο μέλλον μέσα από τη σύνθεση δύο διανυσμάτων θέσης, εκείνης στην οποία θα βρισκόταν εκτελώντας μόνο τη μία κίνηση επί χρόνο t και εκείνης στην οποία θα βρισκόταν εκτελώντας μόνο την άλλη επί τον ίδιο χρόνο t. Αυτά όλα όμως εφόσον οι δύο κινήσεις - στην περίπτωση της βολής, η οριζόντια ευθύγραμμη ομαλή και η κατακόρυφη ομαλά επιταχυνόμενη - είναι ΑΝΕΞΑΡΤΗΤΕΣ, η εξέλιξη δηλαδή της «μιας» δεν αλλοιώνεται από την ύπαρξη της ταυτόχρονης «άλλης».

γ. Ο Νεύτων

Σύνθεση δύο δυνάμεων και ανεξaρτησία κινήσεων

Για τη συνισταμένη δύο δυνάμεων οι οποίες ασκούνται την ίδια στιγμή στο ίδιο υλικό σημείο ισχύει ο λεγόμενος κανόνας του παραλληλογράμμου. Στο σχολικό εργαστήριο μπορούμε να δείξουμε πειραματικά ότι ο κανόνας ισχ ύει, μέσα από την ισορροπία ενός σώματος στο οποίο ασκούνται οι δύο δυνάμεις.

Την, μέσα από τη «στατική» αυτή θεώρηση,

επιβεβαίωση του κανόνα,

την είχε προτείνει ο Φλαμανδός Simon Stevin,

εκατό περίπου χρόνια, πριν ασχοληθεί

με αυτό το ζήτημα ο Νεύτων.

Ο Νεύτων εισηγήθηκε για την έννοια ΔΥΝΑΜΗ μια νέα «δυναμική» θεώρηση, σχετίζοντας την με την κίνηση των σωμάτων και θέτοντας το ερώτημα « τι σημαίνει συνισταμένη δύο δυνάμεων;» σε μια βάση διαφορετική.

Για να το πετύχει εμπιστεύτηκε και την ιδέα του Γαλιλαίου για ανεξαρτησία των ταυτόχρονων κινήσεων, στον πυρήνα της οποίας υπάρχει το . . . « στον ΙΔΙΟ ΧΡΟΝΟ στον οποίο θα έκανε καθεμιά από τις άλλες κινήσεις» και υποστηρίζει ότι εάν δύο δυνάμεις ασκούνται ταυτόχρονα στο ίδιο αρχικά ακίνητο σώμα, το σώμα, σε ορισμένο χρόνο θα διαγράψει τη διαγώνιο ενός παραλληλογράμμου, στον ίδιο χρόνο που θα διέγραφε τις πλευρές, εάν κάθε δύναμη δρούσε ανεξάρτητα από την άλλη.

Φαντάζεται, δηλαδή , δύο κινήσεις που δεν είναι παρατηρήσιμες - μία κίνηση την οποία θα έκανε το σώμα, σε χρόνο t, εαν δρούσε μόνο η μία δύναμη, και μιαν άλλη κίνηση την οποία θα έκανε το ίδιο σώμα, στον ίδιο χρόνο t, εάν δρούσε μόνο η άλλη- , παρατηρεί και καταγράφει την κίνηση που τελικά εκτελεί το σώμα και προτείνει το πόρισμα Ι .

Principia Mathematica . COROLLARIUM I. Corpus viribus conjunctis diagonalem parallelogrammi eodem tem pore describere, quo latera separatis

Στην αγγλική μετάφραση του Andrew Motte

COROLLARY I . A body, acted on by two forces simultaneously, will describe the diagonial of a parallelogram in the same time as 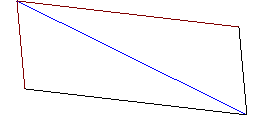it would describe the sides by those forces separately.

ΠΟΡΙΣΜΑ Ι . Ένα σώμα στο οποίο ασκούνται ταυτόχρονα δύο δυνάμεις, θα διαγράψει τη διαγώνιο ενός παραλληλογράμμου στον ίδιο χρόνο που θα διέγραφε τις πλευρές αν οι δυνάμεις αυτές δρούσαν χωριστά.

Συνδυάζοντας, με άλλα λόγια, την, τότε, 100 ετών πρόταση του Stevin, με τη σχετικά νεώτερη ιδέα του Γαλιλαίου και με τη δική του «δυναμική» θεώρηση για την έννοια δύναμη οδηγείται στον κανόνα του παραλληλογράμμου,

ο οποίος, στο μέλλον, θα αποτελέσει και το θεμελιο για τη σύνθεση δύο οποιωνδήποτε διανυσματικών μεγεθών.

Όταν αναζητούμε τη συνισταμένη δύο δυνάμεων δεν πρέπει να ξεχνάμε, ότι καθεμιά από αυτές είναι παράγωγος κάποιας στιγμιαίας ορμής αναφέρεται δηλαδή σε μια κίνηση την οποία ΘΑ ΕΚΑΝΕ το σώμα εάν δρούσε μόνον αυτή

Στα χρόνια που ακολούθησαν, η αρχή της ανεξαρτησίας των ταυτόχρονων κινήσεων οδήγησε τη σκέψη των φυσικών στη λεγόμενη αρχή της υπέρθεσης η οποία είναι ευρύτερη και δεν περιορίζεται μόνο στο φαινόμενο «κίνηση υλικού σημείου».

Η αρχή της ανεξαρτησίας μέσα από τα βιβλία