Ανδρέας Ιωάννου Κασσέτας

Η ΑΡΧΗ ΤΗΣ ΑΝΕΞΑΡΤΗΣΙΑΣ

των ταυτόχρονων κινήσεων Ε.

Ανεξαρτησία των κινήσεων

και μεταβιβαζόμενη ενέργεια

Επιστρέφουμε στο Πόρισμα Ι του Νεύτωνα

Isaac Newton Principia Mathematica

COROLLARY I . A body, acted on by two forces simultaneously, will describe the diagonial of a parallelogram in the same time as it would describe the sides by those forces separately.

ΠΟΡΙΣΜΑ Ι . Ένα σώμα στο οποίο ασκούνται ταυτόχρονα δύο δυνάμεις, θα διαγράψει τη διαγώνιο ενός παραλληλογράμμου στον ίδιο χρόνο που θα διέγραφε τις πλευρές αν οι δυνάμεις αυτές δρούσαν χωριστά.

Θεωρούμε δύο χρονικά σταθερές δυνάμεις την F₁ και την F₂ να ασκούνται ταυτόχρονα σε στο ίδιο, αρχικώς ακίνητο, υλικό σημείο Σ , μάζας m, υπό γωνία 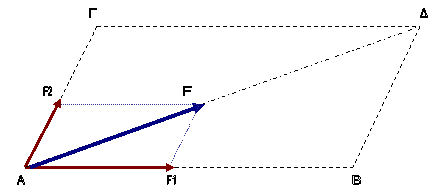θ και τη συνισταμένη τους F.

Σύμφωνα με όσα μας λέει ο Νεύτων, το Σ will describe the diagonial of a parallelogram in the same time as it would describe the sides by those forces separately «θα διαγράψει τη διαγώνιο ενός παραλληλογράμμου στον ίδιο χρόνο που θα διέγραφε τις πλευρές αν οι δυνάμεις αυτές δρούσαν χωριστά»

Ας εστιάσουμε λοιπόν στη νευτωνική επισήμανση «στον ίδιο χρόνο» και ας προσδιορίσουμε την ενέργεια που

θα μεταβίβαζε το περιβάλλον στο Σ στον χρόνο αυτό, έστω t,

α. αν δρούσε μόνο η F₁ , οπότε η μετατόπιση στον χρόνο αυτό θα ήταν ΑΒ = x₁ . W₁ = F₁x₁ . W₁ = F₁.½ α₁t² . Σύμφωνα και με τον δεύτερο νευτωνικό νόμο της κίνησης W₁ = ½F₁²t²/m

β. αν δρούσε μόνο η F₂ οπότε η μετατόπιση στον ίδιο χρόνο θα ήταν ΑΓ = x₂ . το το περιβάλλον θα μεταβίβαζε στο Σ

W₂ = ½F₂²t²/m

Ας προσδιορίσουμε και την ενέργεια που τελικά μεταβιβάζει το περιβάλλον στο Σ με τη δράση της συνισταμένης F στον ίδιο χρόνο κατά τον οποίο το Σ μετατοπίζεται κατά την ΑΔ = x . W = ½F²t²/m.

Διαπιστώνεται ότι το άθροισμα

«ενέργεια που θα μεταβίβαζε η δράση μόνο της F₁ + ενέργεια που θα μεταβίβαζε η δράση μόνο της F₂ » είναι ίσο με «την ενέργεια που τελικά μεταβιβάζεται από την F» , ΜΟΝΟ ΑΝ ΟΙ ΔΥΟ ΣΥΝΙΣΤΩΣΕΣ ΕΙΝΑΙ ΚΑΘΕΤΕΣ ΜΕΤΑΞΥ ΤΟΥΣ.

Στη γενικότερη περίπτωση, δεδομένου ότι F₁² = 2W₁m/t² , F ₂² = 2W₂m/t² , F² = 2Wm/t² και βάσει της Γεωμετρίας F² = F₁² + F₂² + 2 F₁F₂συνθ ,

η σχέση ανάμεσα στις μεταβιβαζόμενες αυτές ποσότητες ενέργειας είναι W = W₁ + W₂ + 2√(W₁ W₂) συνθ .

Αν για τη γωνία θ ισχύει 0≤ < θ < ½π θα είναι W > W₁ + W₂ , η ενέργεια δηλαδή που τελικά μεταβιβάζεται σε χρονικό διάστημα t είναι περισσότερη από το άθροισμα των ενεργειών οι οποίες θα μεταβιβάζονταν αν κάθε μία από τις συνιστώσες δρούσε μόνη της επί το ίδιο χρονικό διάστημα t .

Αν για τη γωνία θ ισχύει π ≧ θ > ½π θα είναι W < W₁ + W₂ στο χρονικό δηλαδή διάστημα t τελικά μεταβιβάζεται λιγότερη ενέργεια από το άθροισμα των ενεργειών οι οποίες θα μεταβιβάζονταν αν κάθε μία από τις συνιστώσες δρούσε μόνη της επί το ίδιο χρονικό αυτό διάστημα t .

Ας δούμε τι συμβαίνει στην ειδική περιπτωση που οι ασκούμενες συνιστώσες δυνάμεις έχουν ίδια κατεύθυνση. Ας υποθέσουμε ότι η συνισταμένη τους είναι F και οι δύο δυνάμεις είναι F₁ = ρF

και F₂ = (ρ-1)F, με 0 < ρ < 1 .

α . Η ενέργεια που θα μεταβίβαζε το περιβάλλον στο Σ σε χρόνο t,

αν δρούσε μόνο η F₁ , οπότε η μετατόπιση, στον χρόνο αυτό, θα ήταν

ΑΒ = x₁ είναι W₁ = F₁ x₁ = ½F₁²t²/m W₁ = F₁ x₁ = ½F²ρ²t²/m

α . Η ενέργεια που τελικά μεταβιβάζεται από το περιβάλλον στο Σ σε χρόνο t, λόγω της δράσης της F₁ , η οποία συνεργάζεται με την F₂ και η μετατόπιση είναι x

είναι W₁ = F₁ x = ½F₁ F t²/m = ½Fρ²t²/m W₁ = ρW₁

Τι σημαίνει αυτό ; Αν μια δύναμη F₁ = F/5 (ρ = 1/5) «συνομωτεί» με μια άλλη δύναμη F₂= 4F/ 5 έτσι ώστε η συνισταμένη τους να είναι F, η ενέργεια W₁

η οποία τελικά μεταβιβάζεται λόγω της δράσης της F₁ θα είναι 5 φορές περισσότερη από όση θα μεταβιβαζόταν εάν η F₁ δρούσε χωρίς την άλλη δύναμη.

Επίλογος . Όταν – δίνοντας έμφαση στην ισότητα των χρόνων – αναλύουμε μια κίνηση σε συνιστώσες κινήσεις ή όταν αναλύομε μια δύναμη σε δύο συνιστώσες, ούτε η αρχή της ανεξαρτησίας των ταυτόχρονων κινήσεων, ούτε η θεωρία – κανόνας του παραλληλογράμμου - για τη σύνθεση των δυνάμεων δεν καλύπτουν το «τι γίνεται με τα ενεργειακά πάρε δώσε του σώματος». Δεν μας λένε, λόγου χάρη, ότι κατά την ανάλυση αυτή «η ενέργεια που μεταβιβάζεται στο κινούμενο υλικό σημείο είναι το άθροισμα των ενεργειών που θα μεταβιβάζονταν στον ίδιο χρόνο αν καθεμιά από τις κινήσεις εκδηλωνόταν χωρίς την άλλη ή αν καθεμιά από τις δυνάμεις δρούσε μόνη της» .

Αντίστοιχα και η - μετά χρόνο t - κινητική ενέργεια του αρχικώς ακίνητου υλικού σημείου, δεν είναι, στη γενική περίπτωση, άθροισμα των κινητικών ενεργειών που θα αποκτούσε εάν έκανε καθεμιά κίνηση ξεχωριστά , επί χρόνο t

Βασιζόμενοι βέβαια στις θεωρίες αυτές και στο εννοιολογικό περιεχόμενο της έννοιας μεταβιβαζόμενη ενέργεια – με μηχανισμό έργου δύναμης - μπορούμε να οδηγηθούμε σε απαντήσεις σε σχετικά ερωτήματα.

Στο συγκεκριμένο ζήτημα ( ανάλυση μιας κίνησης - σύνθεση κινήσεων και ενεργειακό «πάρε δώσε» ) έχει εδώ και μερικά χρονια παρουσιαστεί η - κατά την άποψή μου- ενδιαφέρουσα εργασία του Δημήτρη Τσαούση. Έχει επίσης κάνει αξιοσημείωτες παρατηρήσεις και ο Πάνος Μουρούζης.

Η δική μου, καθυστερημένη, παρέμβαση γίνεται διότι πολλοί εκπαιδευτικοί εξακολουθούν να θέτουν ερωτήματα όπως το

«αν ένα αρχικώς ακίνητο υλικό σημείο συμμετέχει σε δύο κινήσεις ανεξάρτητες, η κινητική του ενέργεια θα είναι ή δεν θα είναι ΑΘΡΟΙΣΜΑ των κινητικών ενεργειών τις οποίες θα αποκτούσε εάν εκτελούσε κάθε κίνηση χωριστά ;» και επειδή αυτό στη γενική περίπτωση ΔΕΝ ισχύει, συμβαίνει να αποδίδουν ευθύνες στην αρχή της ανεξαρτησίας, ενίοτε και να την καταγγέλουν .

Χρειάζεται ίσως να θυμίσω ότι η αρχή της ανεξαρτησίας διακηρύσσοντας ότι «η εξέλιξη μιας ΚΙΝΗΣΗΣ κίνησης δεν αλλοιώνεται από την ύπαρξη μιας άλλης ταυτόχρονης» μας προτείνει, σε περιπτώσεις ανεξάρτητων κινήσεων, τρόπο να προβλέπουμε – μέσα από υπέρθεση - στοιχεία που περιγραφουν την κινητική κατάσταση – όπως η ΘΕΣΗ, η ΤΑΧΥΤΗΤΑ και η ΕΠΙΤΑΧΥΝΣΗ του σώματος Δεν μας προτείνει να εφαρμόσουμε ΥΠΕΡΘΕΣΗ ΜΕ ΚΙΝΗΤΙΚΕΣ ΕΝΕΡΓΕΙΕΣ.

Η αρχή της ανεξαρτησίας των κινήσεων

και το ΟΝΟΜΑ της