Ανδρέας Ιωάννου Κασσέτας

η Στατική τριβή

Στη Φυσική υπάρχουν δύο δυνάμεις με το όνομα ΤΡΙΒΗ.

Η περισσότερο γνωστή είναι η ΤΡΙΒΗ ολίσθησης η οποία αναφέρεται και ως ΤΡΙΒΗ ( χωρίς δηλαδή άλλο προσδιορισμό ).

Η λιγότερο γνωστή είναι η λεγόμενη ΣΤΑΤΙΚΗ ΤΡΙΒΗ η οποία κακώς αναφέρεται ως «ΤΡΙΒΗ».

Τι είναι η ΣΤΑΤΙΚΗ ΤΡΙΒΗ ;

Για τη Φυσική η ΣΤΑΤΙΚΗ ΤΡΙΒΗ είναι ΔΥΝΑΜΗ η οποία δεν έχει σχέση

με την εμπειρία του «δυο σώματα τρίβονται »

Πότε εμφανίζεται ;

Εμφανίζεται στην επαφή δύο σωμάτων τα οποία βρίσκονται σε σχετική ΙΣΟΡΡΟΠΙΑ ενώ συγχρόνως αλληλοσυμπιέζονται

Ποιος είναι ο ρόλος της ;

Περιγράφει το γεγονός ότι τα δύο αντικείμενα ΓΑΝΤΖΩΝΟΝΤΑΙ και εξαιτίας αυτού ακινητούν το ένα ως προς το άλλο.

Μερικοί λένε πως η στατική τριβή δεν είναι τριβή. Τι εννοούν ;

Εννοούν ότι τα δύο σώματα ΔΕΝ ΤΡΙΒΟΝΤΑΙ, ούτε και θερμαίνονται άρα ο όρος στατική ΤΡΙΒΗ δεν εναρμονίζεται με τις αναπαραστάσεις των μαθητών . Το «στατική τριβή» δεν είναι παρά ένας όρος τον οποίο χρησιμοποιεί η Φυσική για μία ΔΥΝΑΜΗ που περιγράφει το «γάντζωμα» των δύο σωμάτων

Πώς είναι η ΚΑΤΕΥΘΥΝΣΗ της ;

Υπάρχει κάποιος κανόνας για να την προσδιορίζουμε ;

1. Η κατεύθυνσή της ι στατικής τριβής είναι ΕΤΣΙ ΩΣΤΕ ΝΑ ΙΣΧΥΟΥΝ ΟΙ ΝΟΜΟΙ.

2. Η ασκούμενη σε ένα σώμα Σ στατική τριβή έχει κατεύθυνση ΑΝΤΙΘΕΤΗ προς εκείνη της ΤΑΧΥΤΗΤΑΣ ΤΗΝ ΟΠΟΙΑ ΘΑ ΑΠΟΚΤΟΥΣΕ ΤΟ Σ εάν η επαφή ήταν λεία

Πιο αυστηρά

Η κατεύθυνση της στατικής τριβής την οποία ασκεί ένα σώμα Σ’ σε ένα σώμα Σ με το οποίο βρίσκεται σε επαφή, συμπιέζεται από αυτό και ακινητεί ως προς αυτό, είναι αντίθετη της κατεύθυνσης που θα είχε η σχετική ταχύτητα την οποία θα αποκτούσε το Σ

( ως προς το Σ’ ) εάν η επαφή ήταν λεία.

Με τον κανόνα αυτόν μπορούμε να βασιστούμε για να εξηγήσουμε πώς γίνεται το περπάτημα

Ο άνθρωπος πιέζει το έδαφος με το πόδι του. Το έδαφος του ασκεί κάθετη αντίδραση και στατική τριβή, αρκεί να «γαντζωθεί» στιγμιαία το πόδι του και να μη γλιστράει.

Ποια είναι η ΤΙΜΗ της στατικής τριβής ;

Το βαρύ κιβώτιο βρίσκεται στο τραπέζι και δεν το πειράζει κανείς.

Οι δυνάμεις που ασκούνται στο κιβώτιο είναι το βάρος και η κάθετη αντίδραση

Αν κάποιος θελήσει να μετακινήσει το κιβώτιο ασκώντας μία μικρή οριζόντια δύναμη F₁ και αποτύχει. για να ερμηνεύσουμε το φαινόμενο ΙΣΟΡΡΟΠΙΑ δεχόμαστε ότι το τραπέζι ασκεί στο κιβώτιο ΣΤΑΤΙΚΗ ΤΡΙΒΗ ίση κατά μέτρο με τη δύναμη F₁ και σε αντίθετη κατεύθυνση. Αν ο «κάποιος» επιμείνει με μεγαλύτερη δύναμη F₂ και το κιβώτιο διατηρηθεί ακίνητο δεχόμαστε ότι το τραπέζι ασκεί στο κιβώτιο ΣΤΑΤΙΚΗ ΤΡΙΒΗ ίση κατά μέτρο με την F₂. Εφόσον το κιβώτιο διατηρείται ακίνητο η στατική τριβή θα είναι ίση κατά μέτρο με την οριζόντια δύναμη

Ναι αλλά θα έρθει κάποια στιγμή που το κιβώτιο θα μετακινηθεί. Για να περιγράψουμε την εμπειρία έτσι ώστε να ισχύουν οι νόμοι δεχόμαστε ότι η επιφάνεια του τραπεζιού μπορεί να ασκεί στατική τριβή και να συγκρατεί το κιβώτιο μέχρις ενός σημείου. Υπάρχει δηλαδή ένα ΜΕΓΙΣΤΟ στην τιμή της στατικής τριβής που μπορεί να ασκεί η επιφάνεια του τραπεζιού.

Οι μετρήσεις δείχνουν ότι η ΜΕΓΙΣΤΗ ΑΥΤΗ ΤΙΜΗ είναι ίση με το γινόμενο της κάθετης αντίδρασης επί ένα συντελεστή μ_σ., τον λεγόμενο «συντελεστή στατικής τριβής» .

T_{σ, max} = μ_σΝ

Για τις τιμές που μπορεί να έχει η στατική τριβή ισχύει 0 ≤ T_{σ, max} ≤ μ_σΝ

Η σχέση T_{σ, max} ≤ μ_σΝ περιγράφει – μαζί με τις εξισώσεις ισορροπίας – το φαινόμενο «σχετική ισορροπία»

Η σχέση T_{σ, max} = μ_σΝ ισχύει όταν «επίκειται ολίσθηση»

Πώς μπορούμε να μετρήσουμε τον συντελεστή στατικής τριβής ;

Μια καλή λύση είναι το ΤΡΙΒΟΜΕΤΡΟ

Βάζουμε το αντικείμενο πάνω στη σανίδα και αρχίζουμε αργά να τη στρέφουμε μέχρι τη στιγμή που το αντικείμενο

θα αρχίσει να γλιστρά προς τα κάτω. Προσδιορίζουμε τη γωνία θ που σχηματίζει εκείνη τη στιγμή η επιφάνεια της σανίδας με το οριζόντιο επίπεδο.

Εφαρμόζουμε τον νόμο της αδράνειας ( mgημθ= Τ_σ και mgσυνθ = Ν )

και τη σχέση T_σ,_max = μ_σ Ν

Καταλήγουμε στη σχέση μ_σ = εφθ.

Με τη γωνία θ στην οποία αρχίζει η ολίσθηση μπορούμε να υπολογίσουμε τον συντελεστή στατικής τριβής καθώς και τη μέγιστη στατική τριβή

Το ξύλινο αντικείμενο γλιστρά όταν η γωνία γίνει 22⁰

και εφόσον εφ22⁰ = 0,4

ο συντελεστής στατικής τριβής είναι 0,4

Η ΣΤΑΤΙΚΗ ΤΡΙΒΗ μπορεί να είναι επιταχύνουσα δύναμη ;

Αν πάνω σε ένα φύλλο χαρτί βάλεις ένα νόμισμα και το τραβήξεις όχι πολύ απότομα, το χαρτί θα συμπαρασύρει το νόμισμα σε μια επιταχυνόμενη κίνηση και η οριζόντια δύναμη που θα ασκείται στο χαρτί θα είναι η ΣΤΑΤΙΚΗ ΤΡΙΒΗ η οποία θα περιγράφει το «γάντζωμα» και θα έχει την κατεύθυνση της επιτάχυνσης σύμφωνα με τον δεύτερο νόμο της κίνησης . Και η τιμή της στατικής τριβής θα είναι ίση με το γινόμενο «μάζα νομίσματος επί την επιτάχυνση». Γι αυτό αν το τραβήξεις το χαρτί ΑΠΟΤΟΜΑ , η στατική τριβή δεν θα μπορέσει να ανταποκριθεί γιατί θα πρέπει να ξεπεράσει το μέγιστο της τιμής της και αυτό απαγορεύεται. Έτσι εξηγείται και το «γιατί» με το ΑΠΟΤΟΜΑ το νόμισμα δεν θα ακολουθήσει το χαρτί.

Γι αυτό κι όταν τραβήξει κανείς ΑΠΟΤΟΜΑ το τραπεζομάντηλο, μπορεί το ποτήρι το πιάτο και το κηροπήγιο να μείνουν στη θέση τους .

Τι εννοούμε λέγοντας ότι «η τιμή και η κατεύθυνση

της στατικής τριβής είναι έτσι ώστε να ισχύουν οι νόμοι» ;

Όταν κυλάει μια μπίλια, χωρίς να γλιστράει το σημείο που κάθε φορά αγγίζει το έδαφος έχει ταχύτητα μηδέν. Η δύναμη που ενδεχομένως θα ασκείται στη μπίλια θα είναι στατική τριβή. Και τόσο η τιμή της όσο και η κατεύθυνσή της θα διαμορφώνονται ΕΤΣΙ ΩΣΤΕ ΝΑ ΙΣΧΥΟΥΝ ΟΙ ΝΟΜΟΙ του φαινομένου ΚΥΛΙΣΗ.

Εάν κατά την κύλιση σε οριζόντιο απόλυτα στερεό έδαφος ασκείται οριζόντια δύναμη F στο ψηλότερο σημείο της σφαίρας, οι νομοι οδηγούν στο συμπέρασμα ότι η στατική τριβή θα έχει την κατεύθυνση της επιτάχυνσης του κέντρου μάζας και μέτρο ίσο με 3F/7

Εάν η κύλιση γίνεται σε οριζόντιο απόλυτα στερεό έδαφος χωρίς τη δράση κάποιας άλλης δύναμης, η ταχύτητα του κέντρου μάζας είναι σταθερή και η στατική τριβή σύμφωνα με τους νόμους πρέπει να είναι μηδενική .

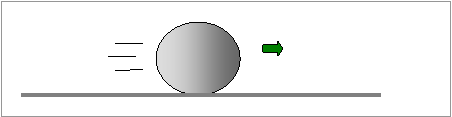
Εάν η μπίλια βρίσκεται σε κεκλιμένο επίπεδο και κυλίεται προς το πάνω, η κατεύθυνση της στατικής τριβής θα είναι προς τα πάνω

Εάν η μπίλια βρίσκεται σε κεκλιμένο επίπεδο και κυλίεται προς το κάτω, η κατεύθυνση της στατικής τριβής θα είναι προς τα πάνω

.

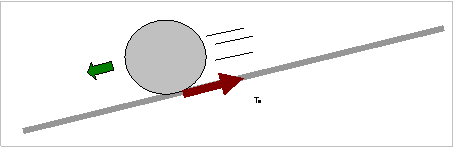
η ΤΡΙΒΗ ολίσθησης

.