ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ΄ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟ

ΚΑΙ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ΄ ΤΑΞΗΣ ΕΠΑΛ ( ΟΜΑΔΑ Β΄)

ΔΕΥΤΕΡΑ 25 ΜΑΙΟΥ 2009

ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ

ΘΕΜΑ 1^Ο

Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1 -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.

1. Σε μια φθίνουσα ταλάντωση της οποίας το πλάτος μειώνεται εκθετικά με τον χρόνο.

α. η ενέργεια του ταλαντωτή είναι συνεχώς σταθερή

β. η συχνότητα αυξάνεται με την πάροδο του χρόνου

γ. Ο λόγος δύο διαδοχικών μεγίστων απομακρύνσεως προς την ίδια κατεύθυνση διατηρείται σταθερός

δ. το πλάτος μειώνεται γραμμικά με τον χρόνο ( Μονάδες 5 )

2. Σε μία απλή αρμονική ταλάντωση η απομάκρυνση και η επιτάχυνση την ίδια χρονική στιγμή

α . έχουν πάντα αντίθετο πρόσημο β. έχουν πάντα το ίδιο πρόσημο

γ. θα έχουν το ίδιο ή αντίθετο πρόσημο ανάλογα με την αρχική φάση της απλής αρμονικής ταλάντωσης

δ. μερικές φορές έχουν το ίδιο και άλλες φορές έχουν αντίθετο πρόσημο ( Μονάδες 5 )

3. Σε στάσιμο κύμα δύο σημεία του ελαστικού μέσου βρίσκονται μεταξύ δύο διαδοχικών δεσμών. Τότε τα σημεία αυτά έχουν

α. διαφορά φάσης π β. την ίδια φάση

γ. διαφορά φάσης που εξαρτάται από την απόστασή τους

δ. διαφορά φάσης π/2 ( Μονάδες 5 )

4. Η περίοδος ταλάντωσης ενός ιδανικού κυκλώματος ηλεκτρικών ταλαντώσεων LC είναι Τ. Διατηρώντας το ίδιο πηνίο, αλλάζουμε τον πυκνωτή χωρητικότητας C₁ με άλλον πυκνωτή χωρητικότητας C₂ = 4C₁. Τότε η περίοδος ταλάντωσης του νέου κυκλώματος θα είναι ίση με:

α. Τ/2 β. 3Τ γ. 2Τ δ. Τ/4 ( Μονάδες 5 )

5. Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα τη λέξη Σωστό για τη σωστή απάντηση και τη λέξη Λάθος για τη λανθασμένη

α. Κατά την είσοδο μιας μονοχρωματικής ακτίνας φωτός από τον αέρα στο νερό είναι δυνατόν να επιτευχθεί ολική ανάκλαση

β. Όταν ένας παρατηρητής πλησιάζει με σταθερή ταχύτητα μια ακίνητη ηχητική πηγή, τότε ακούει ήχο μικρότερης συχνότητας (βαρύτερο) από αυτόν που παράγει η πηγή

γ. Στα στάσιμα κύματα, τα σημεία που παρουσιάζουν μέγιστο πλάτος ταλάντωσης ονομάζονται κοιλίες.

δ. Σε μια εξαναγκασμένη ταλάντωση, η συχνότητα της ταλάντωσης ισούται με τη συχνότητα του διεγέρτη

ε. Η ροπή αδράνειας ενός στερεού σώματος δεν εξαρτάται από τον άξονα περιστροφής του σώματος. ( Μονάδες 5 )

ΘΕΜΑ 2^Ο

Να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.

1. Ο δίσκος του σχήματος κυλίεται χωρίς να ολισθαίνει σε οριζόντιο επίπεδο. Η ταχύτητα του κέντρου του Ο είναι υ_ο .

Το σημείο Α βρίσκεται στην περιφέρεια του δίσκου και το ΑΟ είναι οριζόντιο.

Η ταχύτητα του σημείου Α έχει μέτρο α. υ_Α = 2 υ_ο β. υ_Α = √2 υ_ο γ. υ_Α = υ_ο ( Μονάδες 3 )

Να αιτιολογήσετε την απάντησή σας ( Μονάδες 5 )

2. Σώμα μάζας m_A κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα μέτρου υ_Α και συγκρούεται μετωπικά και πλαστικά με ακίνητο σώμα μάζας m_Β = 2m_A . Η μεταβολή της κινητικής ενέργειας του συστήματος τω δύο σωμάτων, η οποία παρατηρήθηκε κατά την κρούση είναι :

α. ΔΚ = - m_Aυ_Α²/6 β. ΔΚ = - m_Aυ_Α²/3 γ. ΔΚ = - 2m_Aυ_Α²/3 ( Μονάδες 3 )

Να αιτιολογήσετε την απάντησή σας ( Μονάδες 5 )

3. Υλικό σημείο Σ εκτελεί απλή αρμονική ταλάντωση πλάτους Α και κυκλικής συχνότητας ω. Η μέγιστη τομή του μέτρου της ταχύτητας είναι υ₀ και του μέτρου της επιτάχυνσής του είναι α₀. Αν x, υ, α είναι τα μέτρα της απομάκρυνσης της ταχύτητας και της επιτάχυνσης του Σ αντίστοιχα, τότε σε κάθε χρονική στιγμή ισχύει :

α. υ² = ω (Α² – x ²) β. x ² = ω² ( α₀² – α ² ) γ. α ² = ω² ( υ₀² – υ ² )

Να αιτιολογήσετε την απάντησή σας ( Μονάδες 6 )

1. Η κίνηση του δίσκου μπορεί να θεωρηθεί προερχόμενη από τη σύνθεση μιας μεταφορικής με την ταχύτητα υ₀ του κέντρου μάζας και 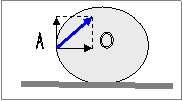μιας στροφικής περί άξονα που διέρχεται από το κέντρο μάζας. Κάθε εξωτερικό σημείο του δίσκου έχει, λόγω στροφικής κίνησης, ταχύτητα υ η οποία είναι και εφαπτόμενη στην κυκλική τροχιά. Εφόσον η κίνηση είναι «κύλιση χωρίς ολίσθηση» τα μέτρα των υ και υ₀ είναι ίσα .

Η λόγω στροφικής κίνησης ταχύτητα του σημείου Α ως εφαπτόμενη στην τροχιά θα είναι κατακόρυφη προς τα πάνω. Εφόσον η κίνηση είναι «κύλιση χωρίς ολίσθηση» τα μέτρα των υ και υ₀ είναι ίσα .

Το σημείο Α έχει συνεπώς ταχύτητα η οποία είναι διανυσματικό άθροισμα της οριζόντιας υ₀ ( ταχύτητας του κέντρου μάζας ) και της ίσου μέτρου κατακόρυφης υ. Άρα υ_Α ² = υ₀²+υ² υ_Α²= 2υ₀ ² υ_Α = √2υ₀

2. Λύση . Αν m_A = m θα είναι m_B = 2m οπότε η μάζα του συσσωματώματος 3m .

Παριστάνουμε με V την κοινή ταχύτητα του συσσωματώματος.

Για το φαινόμενο πλαστική κρούση εφαρμόζουμε τη ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ του συστήματος. mυ + 0 = 3mV άρα V = υ/3

Η μεταβολή της κινητικής ενέργειας θα είναι ΔΚ = ½3mV ² – ½mυ ² . Αν θέσουμε V = υ/3 θα είναι

ΔΚ = ½3mυ ²/9 – ½mυ ² ΔΚ = – mυ²/3

3. Λύση . Οι εξισώσεις της κίνησης είναι οι

υ = υ₀συν(ωt+φ) (1) με υ₀ = ωΑ (2) και α = - ω²Aημ(ωt+φ) (3)

Από τις (1) και (3) , με απαλοιφή του t, ημ²(ωt+φ) = α²/A²ω⁴ συν²(ωt+φ) = υ²/υ₀ ²

προκύπτει η υ²/υ₀² + α²/ω⁴Α² = 1 (4)

Λόγω της (2) θα είναι υ₀² = ω²Α² συνεπώς ω⁴Α² = ω²υ₀². και εάν αντικαταστήσουμε στην (4)

προκύπτει υ²/υ₀² + α²/ ω²υ₀² = 1 οπότε και α ² = ω² ( υ₀² – υ ² )

Το ίδιο βέβαια θα προκύψει και αν βασιστούμε στις υ = υ₀συνωt και α = - ω²Αημωt

Μία λύση αποδεκτή . Η ποσότητα ω (Α² – x ²) δεν έχει διαστάσεις τετραγώνου ταχύτητας. Έχει μονάδα μέτρησης το m²/s

Η ποσότητα ω² ( α₀² – α ² ) δεν έχει διαστάσεις τετραγώνου μήκους. Έχει μονάδα μέτρησης το m²/s⁶

Άρα, εφόσον ένα είναι οπωσδήποτε σωστό, το μόνο που είναι σωστό είναι το α ² = ω² ( υ₀² – υ ² )

Εξάλλου το ω² ( υ₀² – υ ² ) με μονάδα μέτρησης το 1 m²/s⁴ έχει διαστάσεις τετραγώνου επιτάχυνσης

ΘΕΜΑ 3^Ο

Η εξίσωση ενός γραμμικού αρμονικού κύματος που διαδίδεται κατά μήκος του άξονα xx΄είναι y = 0, 4 ημ2π( 2t – 0,5x) ( S.I.)

Να βρείτε α. Το μήκος κύματος λ και την ταχύτητα διάδοσης του κύματος υ. ( Μονάδες 6 )

β. Τη μέγιστη ταχύτητα ταλάντωσης των σημείων του ελαστικού μέσου ( Μονάδες 6 )

γ. Τη διαφορά φάσης που παρουσιάζουν την ίδια χρονική στιγμή δύο σημεία του ελαστικού μέσου, τα οποία απέχουν μεταξύ τους απόσταση ίση με 1,5 m. ( Μονάδες 6 )

δ. Για τη χρονική στιγμή t = 11/8 s να βρείτε την εξίσωση που περιγράφει το στιγμιότυπο του κύματος και στη συνέχεια να τo σχεδιάσετε.

( Το στιγμιότυπο του κύματος να σχεδιαστεί με στυλό ή μολύβι στο μιλιμετρέ ) ( Μονάδες 7 )

α . Η εξίσωση αρμονικού κύματος είναι y = 0, 4 ημ2π(t/T – x/λ) ή y = 0, 4 ημ2π(t/f – x/λ)

Συγκρίνοντας τη δεδομένη y = 0, 4 ημ2π( 2t – 0,5x) με την γενική εξίσωση αρμονικού κύματος y = 0, 4 ημ2π(tf – x/λ)

προκύπτει ότι λ = 2 m και συχνότητα f = 2 Hz άρα σύμφωνα με τη θεμελιώδη εξίσωση των κυμάτων υ = λf η τιμή της ταχύτητας διάδοσης θα είναι 4 m/s.

β. Η μέγιστη ταχύτητα ταλάντωσης είναι ίση με ωΑ ή 2πfA, όπου Α = 0,4 m το πλάτος της ταλάντωσης .

Η μέγιστη ταχύτητα είναι συνεπώς ίση με 1,6π m/s ≈ 5 m/s .

γ. Η φάση ενός σημείου είναι 2π(t/f – x/λ). Την ίδια χρονική στιγμή η φάση ενός άλλου σημείου σε απόσταση d στην κατεύθυνση διάδοσης του κύματος είναι η 2π(t/f – (x+d)/λ)

Άρα η διαφορά φάσης είναι ίση με 2πd/λ. Με d = 1,5 m και με λ = 2 m η διαφορά φάσης θα είναι 3π/2 ή 3π/2 rad

δ. Αν στην εξίσωση y = 0, 4 ημ2π( 2t – 0,5x) θέσουμε t = 11/8 s προκύπτει η συνάρτηση y = 0, 4ημ( 11π/2 – πx) ,

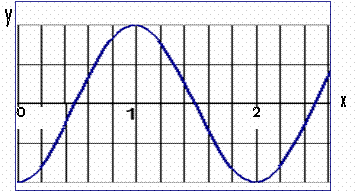
Σχετικά με τα όρια της γραφικής παράστασης υπάρχει ένα πρόβλημα.

Το πρόβλημα υπάρχει εδώ και αρκετά χρόνια αλλά το τρίτο θέμα των φετινών εξετάσεων 2009 το έφερε στην επιφάνεια. Και φαίνεται να οξύνεται από τις κατευθύνσεις προς τους βαθμολογητές «να θεωρήσουν σωστό το στιγμιότυπο κύματος» ΜΟΝΟ εφόσον απεικονίζει το κύμα να υφίσταται από x = 0 μέχρι x=υt = 5,5 m. Το ίδιο ισχύει και για τις λύσεις που προτάθηκαν από διάφορους φροντιστές σε εφημερίδες. Το πρόβλημα

ΘΕΜΑ 4^Ο

Στερεό Π μάζας Μ = 10 kg αποτελείται από δύο κολλημένους ομοαξονικούς κυλίνδρους με ακτίνες R και 2R όπου R= 0,2 m όπως στο σχήμα. Η ροπή αδράνειας του στερεού Π ως προς τον άξονα περιστροφής του είναι Ι = ΜR² . Το στερεό Π περιστρέφεται 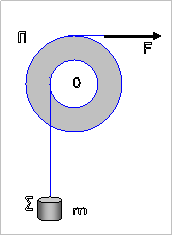χωρίς τριβές γύρω από σταθερό οριζόντιο άξονα Ο΄Ο που συμπίπτει με τον άξονά του. Το σώμα Σ μάζας m = 20 kg κρέμεται από το ελεύθερο άκρο αβαρούς νήματος που είναι τυλιγμένο στον κύλινδρο ακτίνας R. Γύρω από το τμήμα του στερεού Π με ακτίνα 2R είναι τυλιγμένο πολλές φορές νήμα, στο ελεύθερο άκρο Α του οποίου μπορεί να ασκείται οριζόντια δύναμη F.

α. Να βρείτε το μέτρο της αρχικής δύναμης F που ασκείται στο ελεύθερο άκρο Α του νήματος, ώστε το σύστημα που εικονίζεται στο σχήμα να παραμένει ακίνητο. ( Μονάδες 3 )

Τη χρονική στιγμή t₀ = 0 που το σύστημα του σχήματος είναι ακίνητο αυξάνουμε τη δύναμη ακαριαία έτσι ώστε να γίνει F = 115 N

β. Να βρείτε την επιτάχυνση του σώματος Σ . ( Μονάδες 5 )

Για τη χρονική στιγμή που τα σώμα Σ έχει ανέλθει κατά h = 2 m, να βρείτε

γ. το μέτρο της στροφορμής του στερεού Π ως προς τον άξονα περιστροφής του ( Μονάδες 6 )

δ. Τη μετατόπιση του σημείου Α από την αρχική του θέση ( Μονάδες 6 )

ε. Το ποσοστό του έργου της δύναμης F που μετατράπηκε σε κινητική ενέργεια του στερεού Π κατά τη μετατόπιση του σώματος Σ κατά h. ( Μονάδες 5 )

Δίνεται g = 10 m /s² Το συνολικό μήκος κάθε νήματος παραμένει σταθερό

a. Το φαινόμενο ΙΣΟΡΡΟΠΙΑ του συστήματος. Θεωρούμε το σύστημα «στερεό Π, νήματα και σώμα Σ» . Σημειώνουμε τις εξωτερικές δυνάμεις . Είναι η F, η βάρος mg του Σ, η βάρος του Π και δυνάμεις στήριξης ασκούμενες στον άξονα. Εφόσον ισορροπεί η ολική ροπή των δυνάμεων αυτών ως προς οποιοδήποτε σημείο είναι ίση με μηδέν. Επιλέγουμε βέβαια το σημείο Ο. Στ_ο = 0 +F.2R – mg.R =0 F = ½mg F = 100 N .

β. Το φαινόμενο «ανοδική κατακόρυφη ευθύγραμμη κίνηση» του Σ ( θεωρείται υλικό σημείο). Οι ασκούμενες στο Σ δυνάμεις είναι η βάρος mg και μια δύναμη F_ν2 από το τεντωμένο νήμα Ν2 . Εφαρμόζουμε τον δεύτερο νόμο του Νεύτωνα για ευθύγραμμη κίνηση υλικού σημείου. ΣF = ma. F_ν2 - mg = ma (1), όπου α η επιτάχυνση του Σ

Το φαινόμενο «στροφική κίνηση του Π». Οι ασκούμενες στο Σ δυνάμεις είναι η βάρος Μg, μια δύναμη από το και μια δύναμη μέτρου F_ν2 από το κατακόρυφο τεντωμένο νήμα Ν2 και η δύναμη F, ασκούμενη μέσω του νήματος Ν1 . Ασκούνται επίσης δυνάμεις στήριξης με μηδενική ροπή ως προς Ο . Εφαρμόζουμε τον δεύτερο νόμο του Νεύτωνα για ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ στερεού. Επιλέγουμε το σημείο Ο .

Στ_Ο = Ια_γων F.2R - F_ν2 R = Ια_γων . Η επιτάχυνση α του σώματος είναι ίση κατά μέτρο με την επιτρόχια επιτάχυνση των σημείων του στρεφόμενου Π που απέχουν R το οποίο απέχει από τον άξονα.

Ισχύει συνεπώς α = α_γωνR. Με δεδομένο και ότι Ι = ΜR² η σχέση γίνεται F.2R - F_ν2 R = ΜR²α_γων

2F - F_ν2 = ΜRα_γων 2F - F_ν2 = Μα (2), . Από τις (1) και (2) προκύπτει 2F - mg = (Μ+m)α

και α = (2F – mg)/(Μ+m) α = 1 m/s² .

Ορισμένοι από τους εξεταζόμενους – όχι λίγοι – υπολόγισαν τη ζητούμενη τιμή της επιτάχυνσης

με εφαρμογή του δεύτερου νόμου για τη στροφική κίνηση στο ΣΥΣΤΗΜΑ «στερεό Π, νήματα και σώμα Σ» .

Δημιουργήθηκαν διαφωνίες μεταξύ συναδέλφων βαθμολογητών σε πολλά εξεταστικά κέντρα. Άλλοι το θεώρησαν σωστό και άλλοι όχι.

Μπορούμε να το θεωρήσουμε σωστό ;

γ. Η στροφορμή του Π κατά τον άξονα περιστροφής είναι ίση με το γινόμενο Ιω, όπου ω η γωνιακή ταχύτητα.

Ένας τρόπος για να υπολογίσουμε την τιμή της γωνιακής ταχύτητας του Π κατά τη στιγμή που το σώμα Σ έχει ανέβει κατά h είναι να τη συσχετίσουμε με την ταχύτητα του Σ . Ισχύει υ = ω R.

Η ταχύτητα του Σ μπορεί να υπολογιστεί με το θεώρημα έργου ενέργειας στο σώμα Σ .

½ mυ² – 0 = F_ν2 h- mgh ½mυ² = (F_ν2 – mg)h και λόγω του ότι F_ν2 - mg = ma ½mυ² = mah υ = √2αh υ = 2 m/s

( Στην ίδια σχέση υ = √2αh μπορούμε να καταλήξουμε και με το να εφαρμόσουμε εξισώσεις ομαλά επιταχυνόμενης κίνησης για το σώμα Σ υ = αt και h=½ at² . )

Η γωνιακή ταχύτητα του Σ τη στιγμή εκείνη υπολογίζεται από την υ = ωR ω= υ/R ω = 10 rad/s

οπότε η στροφορμή θα είναι L = Iω L = MR²ω L = 4 Js

Μια άλλη λύση. Υπολογίζουμε τη γωνιακή επιτάχυνση του Π . Ισχύει α = α_γωνR άρα α_γων= α/R α_γων= 5 rad/s²

Υπολογίζουμε το χρονικό διάστημα t. h = ½at² άρα t²= 2h/a t =2 s ω = α_γωνt L = MR²α_γωνt L = 4 Js

δ. H ενέργεια W η οποία μεταβιβάζεται στο σύστημα «Π, νήματα, Σ» από τον ασκούντα τη δύναμη F ( ΕΡΓΟ ΤΗΣ F), στη διάρκεια αυτή, είναι η αύξηση της κινητικής ενέργειας και η αύξηση της ( βαρυτικής ) δυναμικής ενέργειας του συστήματος . W = ½mυ² + ½Ιω² + mgh W = 40 J + 20 J + 400 J = 460 J

Η μεταβιβαζόμενη αυτή ενέργεια είναι και ίση και με το γινόμενο Fx , όπου x η ζητούμενη μετατόπιση.

Άρα Fx = W και x = 4 m .

Ισοδύναμος τρόπος είναι το θεώρημα έργου ενέργειας στο σύστημα ½mυ² + ½Ιω² = Fx – mgh και x = 4 m

Μια άλλη λύση. To άκρο Α του νήματος έχει επιτάχυνση α₁ ίση με την επιτρόχια ( γραμμική) επιτάχυνση των σημείων του Π τα οποία απέχουν 2R από τον άξονα. Ισχύει συνεπώς α₁ = α_γων.2R

Το Σ έχει επιτάχυνση α ίση με την επιτρόχια επιτάχυνση των σημείων του Π τα οποία απέχουν R από τον άξονα

α = α_γων.R Άρα η επιτάχυνση του σημείου Α του νήματος είναι διπλάσια από την α του σώματος Σ. Εφόσον σε κινήσεις με σταθερή επιτάχυνση οι μετατοπίσεις -σε ορισμένο χρόνο- είναι ανάλογες προς τις επιταχύνσεις

θα είναι x = 2h και x = 4 m . Αυτό αποτελεί λύση.

Αλλά και με τη χρήση εξισώσεων κίνησης. Για την κίνηση του άκρου Α του νήματος σε χρόνο t x = ½a₁t² .

Η επιτάχυνση α₁ σχετίζεται με τη γωνιακή επιτάχυνση του Π με την α₁ = α_γων.2R

Για την κατακόρυφη επιταχυνόμενη κίνηση του Σ στον ίδιο χρόνο t h = ½at²

Η επιτάχυνση α σχετίζεται με τη γωνιακή επιτάχυνση του Π με την α = α_γων.R

Από τις τέσσερεις αυτές σχέσεις προκύπτει ότι x = 2h και x = 4 m .

ε. Το έργο της δύναμης F υπολογίστηκε W = 460 J

Η κινητική ενέργεια του στρεφόμενου Π ½Ιω² = 20 J

Το % ποσοστό του έργου W που μετετράπη σε κινητική ενέργεια των 20 J 20/460. 100 = 100/23 ≈ 4,38.