Ανδρέας Ιωάννου Κασσέτας

Andreas Ioannou Kassetas

PHILOSOPHIAE NATURALIS

PRINCIPIA MATHEMATICA 3

COROLLARY I

A body, acted on by two forces simultaneously, will describe the diagonial of a parallelogram in the same time as it would describe the sides by those forces separately.

Ένα σώμα στο οποίο σκούνται ταυτόχρονα δύο δυνάμεις, θα διαγράψει τη διαγώνιο ενός παραλληλογράμμου στον ίδιο χρόνο που θα διέγραφε τις πλευρές αν οι δυνάμεις αυτές δρούσαν χωριστά.

Με το ΠΟΡΙΣΜΑ Ι δίνει απάντηση στο ερώτημα «πως θα είναι η κίνηση ενός αρχικά ακίνητου σημειακού αντικειμένου εάν ασκούνται ταυτόχρονα σε αυτό δύο δυνάμεις». Υιοθετεί την παλαιότερη ιδέα του Simon Stevin για το παραλληλόγραμμο των δύο δυνάμεων και την εφαρμόζει στην κίνηση .

COROLLARY II

And hence is explained the composition of any one direct force AD, out of two oblique forces AC and CD;

And, on the contrary, the resolution of any direct force AD into two oblique forces AC and CD ; which composition and resolution re abundantly confirmed from mechanics.

Και έτσι ερμηνεύεται η σύνθεση μιας οποιασδήποτε δύναμης AD από δύο λοξά ασκούμενες δυνάμεις AC και CD.

Και το αντίθετο η ανάλυση μιας δύναμης σε δύο λοξά ασκούμενες δυνάμεις AC και CD.

Για τη σύνθεση και την ανάλυση υπάρχουν άφθονες επιβεβαιώσεις από τη Μηχανική.

Με το ΠΟΡΙΣΜΑ ΙΙ εισάγει τη γενικότερη ιδέα για ΣΥΝΘΕΣΗ οσωνδήποτε δυνάμεων αλλά και την ιδέα για ΑΝΑΛΥΣΗ μιας δύναμης σε δύο συνιστώσες

COROLLARY III

The QUANTITY OF MOTION, which is obtained by taking the sum of MOTIONS directed towards the same parts, and the difference of those that are directed to contrary parts, suffers no change from the action of bodies among themselves.

Η ΟΡΜΗ – ποσότητα κίνησης – η οποία προκύπτει ως άθροισμα δύο ορμών της ίδιας κατεύθυνσης και ως διαφορά ορμών με αντίθετες κατευθύνσεις, δεν υφίσταται μεταβολή από τη δράση – εσωτερικών- δυνάμεων που ασκούνται μεταξύ των σωμάτων

If a spherical BODY A is 3 times greater than the spherical BODY B and has a velocity = 2, and B follows in the same direction with a velocity = 10 , then

the MOTION of A : MOTION of B = 6:10

Εάν ένα σφαρικό σώμα Α είναι 3 φορές μεγαλυτερο από το σφαιρικό σώμα Β και έχει ταχύτητα = 3 και το Β ακολουθεί στην ίδια κατεύθυνση με ταχύτητα = 10, τότε η ΟΡΜΗ του Α : ΟΡΜΗ του Β = 6:10

Με το COROLARY III

α. Πριν απόλα αποσαφηνίζεται το νόημα του όρου MOTION . Με τον όρο MOTUS ο Νεύτων (MOTION o Άγγλος μεταφραστής) υποδηλώνει την έννοια ΟΡΜΗ ενώ για την ορμή ενός συστήματος χρησιμοποιεί το QUANTITY OF MOTION, το αντίστοιχο του γαλλικού quantité de movement το οποίο έχει ήδη χρησιμοποιήσει ο Καρτέσιος και εξακολουθούν να χρησιμοποιούν οι Γάλλοι του σήμερα.

β. Με το CORROLARY III, ο Νεύτων διατυπώνει τη Διατήρηση της ορμής. Την παρουσιάζει βέβαια μόνο για σημειακά αντικείμενα κινούμενα στην ίδια ευθεία ή για σώματα σε μεταφορική κίνηση με τα κέντρα μάζας στην ίδια ευθεία. Η Διατήρηση της ορμής δεν είναι μια ιδέα «δική του» . Κυκλοφορεί ανάμεσα στους Ευρωπαίους στοχαστές ιδίως στου Γάλλους και με περισσή πεποίθηση στο έργο του Καρτέσιου, ο οποίος με αφετηρία το φαινόμενο «κρούση» οδηγήθηκε στη σκέψη ότι είναι αναγκαία η διατήρηση της ορμής.

C'est d'ailleurs l'étude des chocs qui a conduit Descartes à penser qu'une certaine quantité du mouvement était nécessairement conservée.

Ο Νεύτων θα υιοθετήσει τη «Διατήρηση της ορμής» , θα την επεκτείνει σε οποιοδήποτε σύστημα και θα επιχειρήσει να αποδείξει ότι η σχετική «Αρχή» εναρμονίζεται με τους τρεις νόμους της κίνησης. Θα χρησιμοποιήσει μάλιστα τη Διατήρηση της ορμής για να πείσει ότι ισχύει ο τρίτος νόμος της κίνησης.

COROLLARY IV

The common centre of gravity of two or more bodies does not alter its STATE OF MOTION or rest by the actions of the bodies among themselves ; and therefore the common centre of gravity of all bodies acting upon each other ( excluding external actions and its impediments ) is either at rest, or moves uniformly in a right line.

Το κέντρο βάρους δύο ή περισσότερων σωμάτων δεν υφίσταται αλλαγή στην κατάσταση της κίνησης ή της ακινησίας του από τις δράσεις τις ασκούμενες μεταξύ αυτών των σωμάτων. Και γι αυτό το κέντρο βάρους όλων των σωμάτων που αλληλεπιδρούν μεταξύ τους ( εξαιρούνται οι εξωτερικές δράσεις και οι επιβραδύνσεις τους ) είτε είναι ακίνητο είτε εκτελεί ευθύγραμμη ομοιόμορφη κίνηση.

Ο όρος «MOTION of a body» όπως και ο «QUANTITY OF MOTION of a body» παραπέμπει στo ΟΡΜΗ ενός σώματος ενώ

ο όρος STATE OF MOTION of a body παραπέμπει στo φαινόμενο

«ΚΙΝΗΣΗ ενός σώματος».

Με το ΠΟΡΙΣΜΑ IV φωτίζει την ιδιαίτερη σημασία της έννοιας ΚΕΝΤΡΟ ΜΑΖΑΣ για την περίπτωση ενός συστήματος στο οποίο δεν δρουν εξωτερικές δυνάμεις. Βέβαια χρησιμοποιεί τον όρο κέντρο βάρους.

Η εννοιακή διαφορά «κέντρο μάζας – κέντρο βάρους» θα αποσαφηνιστεί λίγες δεκαετίες αργότερα από τον Leonhard Euler στο έργο του Μηχανική

Η χρήση του among – αντί για το between - φανερώνει ότι τα σώματα που συνιστούν το σύστημα δεν είναι υποχρεωτικά μόνο δύο.

COROLLARY V

The motion of bodies included in a given space are the same among themselves, whether the space is at rest, or moves uniformly forwards in a right line without any circular motion

Η κίνηση των σωμάτων που περιέχοντα σε δεδομένο χώρο - Σύστημα αναφοράς - είναι η ίδια, είτε ο χώρος - το Σύστημα αναφοράς- βρίσκεται σε ακινησία, είτε σε ευθύγραμμη ομοιομορφη κίνηση χωρίς καμία κυκλική κίνηση

Με το ΠΟΡΙΣΜΑ V εισάγει την έννοια ΑΔΡΑΝΕΙΑΚΟ ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ.

COROLLARY VΙ

Αναφέρεται στη σχετική κίνηση δύο σωμάτων με ίσες επιταχύνσεις

Για να κλείσει με περίφημο SCHOLIUM με το οποίο επιδιώκει να πείσει για την ισότητα (των μέτρων) δράσης και αντίδρασης (Σελ. 21-28)

PRINCIPIA, p. 25 SCHOLIUM. αγγλική μετάφραση, Andrew Motte	Απόδοση στα ελληνικά Ανδρέας Ιωάννου Κασσέτας	Παρατηρήσεις Ανδρέας Ιωάννου Κασσέτας
In attractions, I briefly demonstrate the thing after this manner. Suppose an obstacle is interposed to hinder the meeting of any two bodies A, B attracting one the other : then if either body, as A, is more attracted towards the other body B, than that other body B is towards the first body A, the obstacle will be more strongly urged by the pressure of the body A than by the pressure of the body B, and therefore will not remain in equilibrium: but the stronger pressure will prevail and will make the system of the two bodies, together with the obstacle, to move directly towards the parts on which B lies ; and in free spaces to go forward in infinitum with a motion continually accelerated ; which is absurd and contrary to the first Law. For, by the first Law the system ought to continue in its state of rest, or of moving uniformly forwards in a right line; and therefore the bodies must equally press the obstacle, and be equally attracted one by the other.	Για ελκτικές δυνάμεις, το αποδεικνύω εν συντομία με τον ακόλουθο τρόπο. Υποθέτουμε ότι ένα εμπόδιο παρεμβάλλεται για να αποτρέψει τη συνάντηση δύο σωμάτων Α και Β τα οποία έλκονται αμοιβαία. Εάν κάποιο από τα δύο σώματα, ας πούμε το Α, έλκεται προς την πλευρά του άλλου σώματος Β ισχυρότερα από όσο το Β έλκεται προς τη μεριά του Α, το εμπόδιο θα σπρώχνεται πιο έντονα από το Α παρά από το Β γι αυτό και δεν θα διατηρηθεί σε ισορροπία. Η ισχυρότερη από τις δύο πιέσεις θα επικρατήσει και θα αναγκάσει το σύστημα των δύο σωμάτων μαζί με το εμπόδιο να κινείται κατευθείαν προς τη μεριά που βρίσκεται το Β και σε ελεύθερο χωρίς δυνάμεις χώρο να προχωρεί επ’ άπειρον, με κίνηση συνεχώς επιταχυνόμενη, το οποίο είναι παράλογο και αντίθετο προς τον πρώτο Νόμο. Διότι, σύμφωνα με τον πρώτο Νόμο, το σύστημα έπρεπε να διατηρείται σε κατάσταση ισορροπίας ή ευθύγραμμης ομοιόμορφης κίνησης. Και γι αυτό τα σώματα πρέπει να πιέζουν εξίσου το εμπόδιο και να έλκονται εξίσου το ένα από το άλλο.	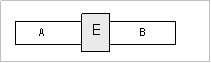Ο Newton παρουσιάζει αρχικά ένα νοητικό πείραμα με δύο σώματα Α και Β και ένα μεταξύ τους εμπόδιο. Τα σώματα έλκονται αμοιβαία και από απόσταση και το Ε εμποδίζει την προσέγγισή τους . 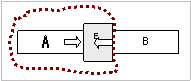εο Β στο Α ΑΠΟΔΕΧΕΤΑΙ ότι ΕΑΝ η έλξη που ασκεί το Β στο Α είναι ισχυρότερη, το εμπόδιο θα σπρώχνεται πιο έντονα από το Α. Από κει και πέρα το εμπόδιο θα εκδήλωνε μετακίνηση και εφόσον αυτό δεν συμβαίνει οδηγείται στην ισότητα FAB = - FBA Αποδέχεται με άλλα λόγια ότι η εξ αποστάσεως δράση του Β στο Α διαβιβάζεται αναλλοίωτη στο σώμα Ε. Η δική μας άποψη είναι ότι η ΑΠΟΔΟΧΗ αυτή εμπεριέχει την ισότητα την οποία θέλει να αποδείξει. Αν έχουμε μια τσιμεντοκολώνα στο πάτωμα – σε αδρανειακό σύστημα – ΑΠΟΔΕΙΚΝΥΕΤΑΙ ότι η δύναμη mg ( βάρος ) που της ασκεί η Γη είναι ίση με τη δύναμη Fτσ, εδ την οποία ασκεί η τσιμεντοκολώνα στο έδαφος αλλά για την απόδειξη θα χρειαστεί να επικαλεστούμε τον νόμο της αδράνειας βάσει του οποίου mg = - Fεδ,τσ και τον τρίτο νόμο βάσει του οποίου Fεδ,τσ = -Fτσ, εδ Η απόδειξη της ισότητας (μέτρων) δράσης και αντίδρασης θα μπορούσε να ΠΡΟΚΥΨΕΙ με βάση τον παρακάτω συλλογισμό: Θεωρούμε την ισορροπία του συστήματος « σώμα Α και εμπόδιο Ε». Οι ασκούμενες εξωτερικές δυνάμεις είναι η ελκτική από το Β ( στο Α ) και η «πιεστική» από το Β στο εμπόδιο FBA = - FΠΒε Θεωρούμε την ισορροπία του συστήματος « σώμα Β και εμπόδιο Ε». Οι ασκούμενες εξωτερικές δυνάμεις είναι η ελκτική από το Α ( στο Β ) και η «πιεστική» από το Α στο εμπόδιο - FAΒ = FΠΑε Θεωρούμε την ισορροπία του εμποδίου Ε . Οι ασκούμενες δυνάμεις είναι η πιεστική FΠΒε από το Β και η πιεστική FΠΑε από το Α . FΠΒε = - FΠΑε Από τις τρεις αυτές ισότητες προκύπτει ότι FBA = - FAΒ Βέβαια εδώ μπορεί να υποβληθεί «ένσταση» για το εάν η ΑΠΟΔΟΧΗ των εξωτερικών και μόνο δυνάμεων σε ένα σύστημα δύο σωμάτων τα οποία αλληλοσυμπιέζονται εμπεριέχει την ισότητα (μέτρων) δράσης αντίδρασης
I made the experiment on the loadstone and iron. If these, placed apart in proper vessels, are made to float by one another in standing water, neither of them will propel the other; but, by being equally attracted, they will sustain each other’ s pressure, and rest at last in equilibrium.	Έκανα το πείραμα με μαγνήτη και σίδερο. Εάν τα δύο αυτά αντικείμενα, τοποθετημένα σε απόσταση πάνω σε κατάλληλα σκάφη είναι φτιαγμένα έτσι ώστε να πλέουν το ένα προς άλλο, σε ακίνητο νερό, κανένα από τα δύο δεν θα μετακινήσει το άλλο, αλλά, ελκόμενα εξίσου, καθένα από αυτά θα υφίσταται την πίεση του άλλου και θα διατηρούνται τελικά σε ισορροπία .	Το πείραμα το οποίο μας λέει ότι πραγματοποίησε αναφέρεται σε μαγνήτη και σίδερο πάνω σε κατάλληλα σκάφη αλλά χωρίς εμπόδιο . Διαπίστωσε ότι τα δύο αντικείμενα διατηρούνται σε ισορροπία μολονότι καθένα από αυτά έλκει το άλλο εξ αποστάσεως και συγχρόνως το σπρώχνει. Η γνώμη μας είναι ότι βασιζόμενοι α. στην εμπειρία της ισορροπίας αλλά και β. στο θεωρητικό δεδομένο ότι η ισότητα (μέτρων) δράσης αντίδρασης ισχύει για πιεστικές δυνάμεις επαφής - όπως έχει δηλώσει στα πρώτα σχόλια για τον νόμο - μπορούμε να οδηγηθούμε στο συμπέρασμα ότι η ισότητα δράσης αντίδρασης ισχύει και για ελκτικές δυνάμεις από απόσταση. Με άλλα λόγια από το συγκεκριμένο πείραμα δεν απορρέει ο νόμος δράσης αντίδρασης. Στο σίδερο ασκείται η ελκτική δύναμη Fμσ από τον μαγνήτη και η μια πιεστική δύναμη FΠμσ με την οποία το σπρώχνει ο μαγνήτης. Εφόσον το σίδερο ισορροπεί Fμσ = - FΠμσ Αντίστοιχα για την ισορροπία του μαγνήτη ισχύει - Fσμ = FΠσμ Αν αποδεχθούμε την ισότητα FΠμσ = - FΠσμ θα οδηγηθούμε και στην ισότητα Fμσ = - Fσμ

Η ΚΙΝΗΣΗ ΤΩΝ ΣΩΜΑΤΩΝ

Βιβλίο1, Βιβλίο 2