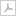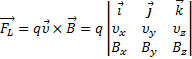Φυσική και Φωτογραφία - 3D κίνηση φορτίου σε μαγνητικό πεδίο

Δημοφιλή

Επιλογές

Αρχική

Φυσική

Γεωγραφία - Χημεία

Πίνακας Περιεχομένων

Φωτογραφικά Αφιερώματα

Πανοραμικές Φωτογραφίες

Τεχνικά Θέματα

Download

Πηγές Ειδήσεων

Σύνδεσμοι Εκπαίδευσης

Αναζήτηση

Τα Δημοφιλέστερα του Μήνα

Σχόλια - Παρατηρήσεις

Για σχόλια, παρατηρήσεις, διορθώσεις, αβλεψίες κλπ μη διστάσετε να επικοινωνήστε μαζί μου. Όσες προσομοιώσεις φέρουν το όνομά μου είναι ελεύθερες προς χρήση και τροποποίηση από όλους, αρκεί να μην αλλαχθούν τα σύμβολα πνευματικής ιδιοκτησίας. Τα αρχεία μπορείτε να τα βρείτε στο menu Download.

Αν θέλετε να χρησιμοποιήσετε τις γραφικές παραστάσεις από τις προσομοιώσεις σε δικές σας εργασίες, να αποθηκεύσετε κάποια προσομοίωση ή να εκτυπώσετε ένα άρθρο κάντε κλικ εδώ για να δείτε την διαδικασία.

Για ενσωμάτωση αρχείων προσομοιώσεων στο Word-Excel-PowerPoint πατήστε εδώ

Σας Ευχαριστώ.

Με δυο λόγια

Τυλίγουμε ένα παγάκι με μάλλινο ύφασμα και το αφήνουμε να λιώσει. Θα λιώσει άραγε πιο γρήγορα επειδή είναι τυλιγμένο σε μάλλινο ύφασμα;

Όχι! Το μάλλινο ύφασμα είναι μονωτής εμποδίζοντας την θερμότητα να μπει αλλά και να βγει. Γι αυτό φοράμε μάλλινα τον χειμώνα. Το ύφασμα λειτουργεί σαν ασπίδα, το απομονώνει από το περιβάλλον του. Έτσι όταν το παγάκι είναι τυλιγμένο με μάλλινο ύφασμα δεν μπορεί να μπεί θερμότητα (από το πιο ζεστό περιβάλλον) με αποτέλεσμα να λιώνει πιο αργά.

Αρχική

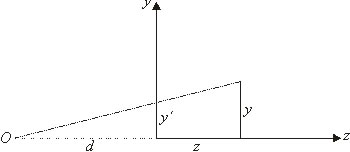
Τεχνικά Θέματα

3D κίνηση φορτίου σε μαγνητικό πεδίο

Ιούλ

2009

3D κίνηση φορτίου σε μαγνητικό πεδίο

(2 ψήφοι)

Το φορτίο q καθώς κινείται μέσα σε μαγνητικό πεδίο

Δέχεται δύναμη Lorentz

που μαζί με την ηλεκτρική δύναμη του προκαλούν επιτάχυνση

Έχοντας τις συνιστώσες της επιτάχυνσης μπορούμε να βρούμε (με την μέθοδο Runge-Kutta) σε κάθε χρονική στιγμή την θέση (x,y,z) του φορτίου. (Να σημειωθεί ότι το μαγνητικό πεδίο δεν χρειάζεται να είναι ομογενές)

Με προοπτική προβολή μπορούμε να προβάλουμε το σημείο αυτό σε σημείο του επιπέδου xy ως εξής :

Από τα όμοια τρίγωνα

όμοια

Αν θέλουμε να δούμε την όλη εικόνα από άλλη οπτική γωνία περιστρέφουμε το σημείο και το προβάλλουμε ξανά στο επίπεδο xy. Για την περιστροφή ενός σημείου (x,y,z) γύρω από το μοναδιαίο διάνυσμα (e₁,e₂,e₃) κατά γωνία θ (τυχαίος άξονας) χρησιμοποιούμε τον παρακάτω πίνακα στροφής.