Τα Μαθήματα του Νέου Λυκείου
- Details
- Category: catlykeio
- Published on 01 September 2014
- Written by Super User
- Hits: 241
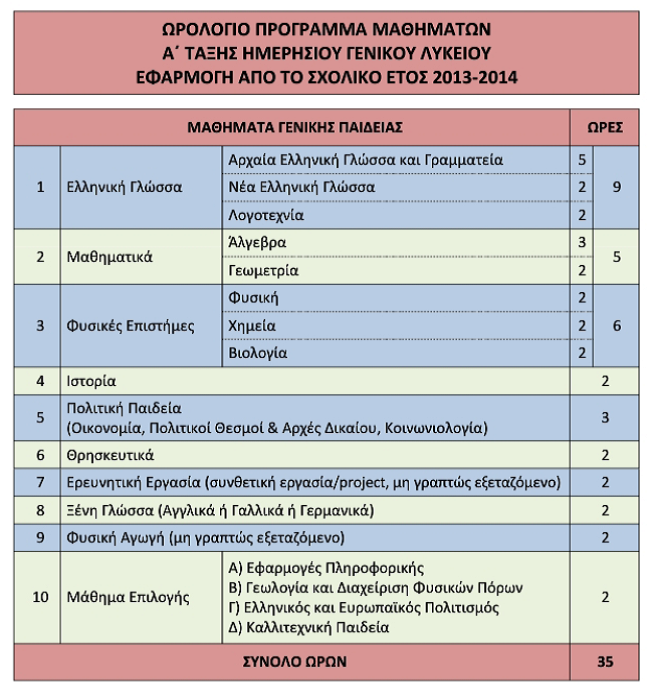

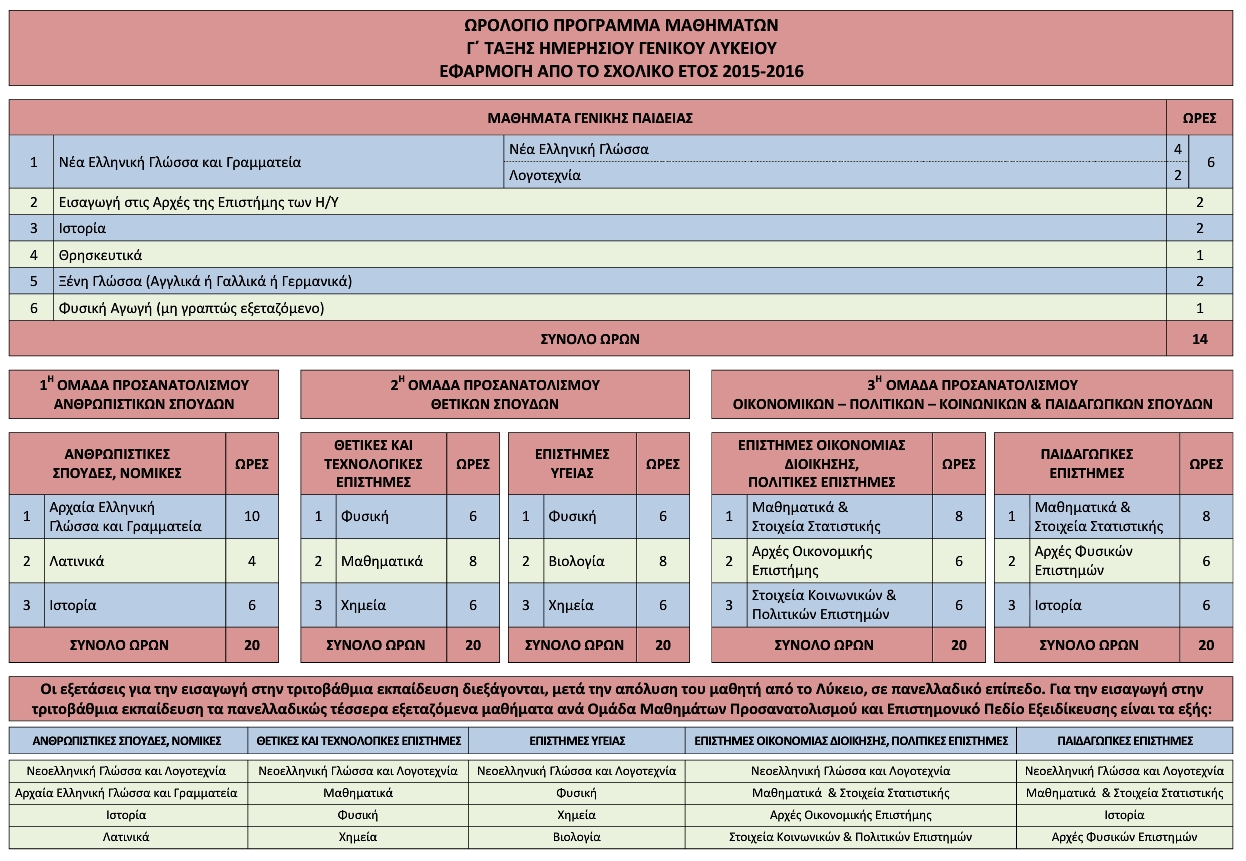
Τα Μαθηματικά στο Νέο Λύκειο περιλαμβάνουν:
 Α΄ Λυκείου. Ισχύει από το Σχολ. Έτος 2013 - 2014
Α΄ Λυκείου. Ισχύει από το Σχολ. Έτος 2013 - 2014
|
Άλγεβρα |
3 ώρες την εβδομάδα |
|
Γεωμετρία |
2 ώρες την εβδομάδα |
| Σύνολο |
5 ώρες την εβδομάδα |
 Β΄ Λυκείου Μαθήματα Γενικής Παιδείας. Ισχύει από το Σχολ. Έτος 2014 - 2015
Β΄ Λυκείου Μαθήματα Γενικής Παιδείας. Ισχύει από το Σχολ. Έτος 2014 - 2015
|
Άλγεβρα |
3 ώρες την εβδομάδα |
|
Γεωμετρία |
2 ώρες την εβδομάδα |
| Σύνολο |
5 ώρες την εβδομάδα |
Β΄ Λυκείου 2η Ομάδα Προσ/μου Θετικών Σπουδών
| Μαθηματικά | 2 ώρες την εβδομάδα |
 Γ΄ Λυκείου. Ισχύει από το Σχολ. Έτος 2015 - 2016
Γ΄ Λυκείου. Ισχύει από το Σχολ. Έτος 2015 - 2016
2η Ομάδα Προσ/μου Θετικών Σπουδών
Επιστημονικό Πεδίο: Θετικές και Τεχνολογικές Επιστήμες
| Μαθηματικά | 8 ώρες την εβδομάδα |
3η Ομάδα Προσ/μου Οικονομικών - Πολιτικών - Κοινωνικών και Παιδαγωγικών Σπουδών
| Μαθηματικά και Στοιχεία Στατιστικής | 8 ώρες την εβδομάδα |
Α' Λυκείου Άλγεβρα
- Details
- Category: catlykeio
- Published on 05 July 2014
- Written by Super User
- Hits: 785
| Σχολικό Βιβλίο | Τίτλος Βιβλίου | Εβδομαδιαίες Ώρες Διδασκαλίας |
 |
Τρείς (3) |
| Περιεχόμενα |
Διδακτέα ύλη 2013 - 2014 | Διαχείριση Διδακτέας ύλης |
|
ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ 1°: Πιθανότητες ΚΕΦΑΛΑΙΟ 2°: Οι Πραγματικοί Αριθμοί ΚΕΦΑΛΑΙΟ 3°: Εξισώσεις ΚΕΦΑΛΑΙΟ 4°: Ανισώσεις ΚΕΦΑΛΑΙΟ 5°: Πρόοδοι ΚΕΦΑΛΑΙΟ 6°: Βασικές Έννοιες των Συναρτήσεων ΚΕΦΑΛΑΙΟ 7°: Μελέτη Βασικών Συναρτήσεων ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ ΥΠΟΔΕΙΞΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ |
Εισαγωγικό κεφάλαιο E.2. Σύνολα Κεφ.1ο: Πιθανότητες 1.1 Δειγματικός Χώρος-Ενδεχόμενα 1.2 Έννοια της Πιθανότητας (εκτός της υποπαραγράφου «Αξιωματικός Ορισμός Πιθανότητας») Κεφ.2ο: Οι Πραγματικοί Αριθμοί 2.1 Οι Πράξεις και οι Ιδιότητές τους 2.2 Διάταξη Πραγματικών Αριθμών (εκτός της απόδειξης της ιδιότητας 4) 2.3 Απόλυτη Τιμή Πραγματικού Αριθμού 2.4 Ρίζες Πραγματικών Αριθμών (εκτός των αποδείξεων των ιδιοτήτων 3 και 4) Κεφ.3ο: Εξισώσεις 3.1 Εξισώσεις 1ου Βαθμού 3.2 Η Εξίσωση xv=α 3.3 Εξισώσεις 2ου Βαθμού Κεφ.4ο: Ανισώσεις 4.1 Ανισώσεις 1ου Βαθμού 4.2 Ανισώσεις 2ου Βαθμού Κεφ.5ο: Πρόοδοι 5.1 Ακολουθίες 5.2 Αριθμητική πρόοδος (εκτός της απόδειξης για το Sν) 5.3 Γεωμετρική πρόοδος (εκτός της απόδειξης για το Sν) Κεφ.6ο: Βασικές Έννοιες των Συναρτήσεων 6.1 Η Έννοια της Συνάρτησης 6.2 Γραφική Παράσταση Συνάρτησης (εκτός της υποπαραγράφου «Απόσταση σημείων») 6.3 Η Συνάρτηση f(x)= αx+β (εκτός της κλίσης ευθείας ως λόγος μεταβολής) Κεφ.7ο: Μελέτη Βασικών Συναρτήσεων 7.1 Μελέτη της Συνάρτησης : f(x)= αx2 7.3 Μελέτη της Συνάρτησης : f(x)= αx2+βx+γ
|
Εισαγωγικό Κεφάλαιο ( 2 ώρες) Κεφάλαιο 1ο (Προτείνεται να διατεθούν 8 διδακτικές ώρες) Κεφάλαιο 2ο (Προτείνεται να διατεθούν 16 διδακτικές ώρες) Κεφάλαιο 3ο (Προτείνεται να διατεθούν 12 διδακτικές ώρες) Κεφάλαιο 4ο (Προτείνεται να διατεθούν 8 διδακτικές ώρες) Κεφάλαιο 5ο (Προτείνεται να διατεθούν 12 διδακτικές ώρες) Κεφάλαιο 6ο (Προτείνεται να διατεθούν 9 διδακτικές ώρες) Κεφάλαιο 7ο (Προτείνεται να διατεθούν 9 διδακτικές ώρες) ΣύνολαΣΥΝΟΛΑ: 76 ΩΡΕΣ ΕΒΔΟΜΑΔΕΣ: 26 ΜΗΝΕΣ ΚΑΤΑ ΠΡΟΣΕΓΓΙΣΗ: 6,5
|
| Περιεχόμενα |
Διδακτέα ύλη 2014 - 2015 | Διαχείριση Διδακτέας ύλης |
|
ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ 1°: Πιθανότητες ΚΕΦΑΛΑΙΟ 2°: Οι Πραγματικοί Αριθμοί ΚΕΦΑΛΑΙΟ 3°: Εξισώσεις ΚΕΦΑΛΑΙΟ 4°: Ανισώσεις ΚΕΦΑΛΑΙΟ 5°: Πρόοδοι ΚΕΦΑΛΑΙΟ 6°: Βασικές Έννοιες των Συναρτήσεων ΚΕΦΑΛΑΙΟ 7°: Μελέτη Βασικών Συναρτήσεων ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ ΥΠΟΔΕΙΞΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ |
Εισαγωγικό κεφάλαιο E.2. Σύνολα Κεφ.1ο: Πιθανότητες 1.1 Δειγματικός Χώρος-Ενδεχόμενα 1.2 Έννοια της Πιθανότητας (εκτός της υποπαραγράφου «Αξιωματικός Ορισμός Πιθανότητας») Κεφ.2ο: Οι Πραγματικοί Αριθμοί 2.1 Οι Πράξεις και οι Ιδιότητές τους 2.2 Διάταξη Πραγματικών Αριθμών (εκτός της απόδειξης της ιδιότητας 4) 2.3 Απόλυτη Τιμή Πραγματικού Αριθμού 2.4 Ρίζες Πραγματικών Αριθμών (εκτός των αποδείξεων των ιδιοτήτων 3 και 4) Κεφ.3ο: Εξισώσεις 3.1 Εξισώσεις 1ου Βαθμού 3.2 Η Εξίσωση xv=α 3.3 Εξισώσεις 2ου Βαθμού Κεφ.4ο: Ανισώσεις 4.1 Ανισώσεις 1ου Βαθμού 4.2 Ανισώσεις 2ου Βαθμού Κεφ.5ο: Πρόοδοι 5.1 Ακολουθίες 5.2 Αριθμητική πρόοδος (εκτός της απόδειξης για το Sν) 5.3 Γεωμετρική πρόοδος (εκτός της απόδειξης για το Sν) Κεφ.6ο: Βασικές Έννοιες των Συναρτήσεων 6.1 Η Έννοια της Συνάρτησης 6.2 Γραφική Παράσταση Συνάρτησης (εκτός της υποπαραγράφου «Απόσταση σημείων») 6.3 Η Συνάρτηση f(x)= αx+β (εκτός της κλίσης ευθείας ως λόγος μεταβολής) Κεφ.7ο: Μελέτη Βασικών Συναρτήσεων 7.1 Μελέτη της Συνάρτησης : f(x)= αx2 7.3 Μελέτη της Συνάρτησης : f(x)= αx2+βx+γ
|
Εισαγωγικό Κεφάλαιο (2 ώρες) Κεφάλαιο 1ο (Προτείνεται να διατεθούν 8 διδακτικές ώρες) Κεφάλαιο 2ο (Προτείνεται να διατεθούν 16 διδακτικές ώρες) Κεφάλαιο 3ο (Προτείνεται να διατεθούν 12 διδακτικές ώρες) Κεφάλαιο 4ο (Προτείνεται να διατεθούν 8 διδακτικές ώρες) Κεφάλαιο 5ο (Προτείνεται να διατεθούν 12 διδακτικές ώρες) Κεφάλαιο 6ο (Προτείνεται να διατεθούν 9 διδακτικές ώρες) Κεφάλαιο 7ο (Προτείνεται να διατεθούν 9 διδακτικές ώρες) ΣύνολαΣΥΝΟΛΑ: ΩΡΕΣ 76 ΕΒΔΟΜΑΔΕΣ: 26 ΜΗΝΕΣ ΚΑΤΑ ΠΡΟΣΕΓΓΙΣΗ: 6.5
|
Α' Λυκείου Γεωμετρία
- Details
- Category: catlykeio
- Published on 05 July 2014
- Written by Super User
- Hits: 342
| Σχολικό Βιβλίο | Τίτλος Βιβλίου | Εβδομαδιαίες Ώρες Διδασκαλίας |
 |
Δύο (2) |
| Περιεχόμενα - Σελίδες |
Διδακτέα ύλη 2013 - 2014 | Διαχείριση Διδακτέας ύλης |
|
|
Κεφ.1ο: Εισαγωγή στην Ευκλείδεια Γεωμετρία 1.1 Το αντικείμενο της Ευκλείδειας Γεωμετρίας 1.2 Ιστορική αναδρομή στη γένεση και ανάπτυξη της Γεωμετρίας Κεφ.3ο: Τρίγωνα 3.1 Είδη και στοιχεία τριγώνων 3.2 1ο Κριτήριο ισότητας τριγώνων (εκτός της απόδειξης του θεωρήματος) 3.3 2ο Κριτήριο ισότητας τριγώνων 3.4 3ο Κριτήριο ισότητας τριγώνων 3.5 Ύπαρξη και μοναδικότητα καθέτου (εκτός της απόδειξης του θεωρήματος) 3.6 Κριτήρια ισότητας ορθογώνιων τριγώνων 3.7 Κύκλος - Μεσοκάθετος ? Διχοτόμος 3.8 Κεντρική συμμετρία 3.9 Αξονική συμμετρία 3.10 Σχέση εξωτερικής και απέναντι γωνίας (εκτός της απόδειξης του θεωρήματος) 3.11 Ανισοτικές σχέσεις πλευρών και γωνιών 3.12 Tριγωνική ανισότητα 3.13 Κάθετες και πλάγιες 3.14 Σχετικές θέσεις ευθείας και κύκλου 3.15 Εφαπτόμενα τμήματα 3.16 Σχετικές θέσεις δύο κύκλων 3.17 Απλές γεωμετρικές κατασκευές 3.18 Βασικές κατασκευές τριγώνων Κεφ.4ο: Παράλληλες ευθείες 4.1. Εισαγωγή 4.2. Τέμνουσα δύο ευθειών - Ευκλείδειο αίτημα 4.3. Κατασκευή παράλληλης ευθείας 4.4. Γωνίες με πλευρές παράλληλες 4.5. Αξιοσημείωτοι κύκλοι τριγώνου 4.6. Άθροισμα γωνιών τριγώνου 4.7. Γωνίες με πλευρές κάθετες 4.8. Άθροισμα γωνιών κυρτού ν-γώνου Κεφ.5ο: Παραλληλόγραμμα - Τραπέζια 5.1. Εισαγωγή 5.2. Παραλληλόγραμμα 5.3. Ορθογώνιο 5.4. Ρόμβος 5.5. Τετράγωνο 5.6. Εφαρμογές στα τρίγωνα 5.7. Βαρύκεντρο τριγώνου (εκτός της απόδειξης του θεωρήματος) 5.8. Το ορθόκεντρο τριγώνου 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου 5.10. Τραπέζιο 5.11. Ισοσκελές τραπέζιο 5.12. Αξιοσημείωτες ευθείες και κύκλοι τριγώνου Κεφ.6ο: Εγγεγραμμένα σχήματα 6.1. Εισαγωγικά ? Ορισμοί 6.2. Σχέση εγγεγραμμένης και αντίστοιχης επίκεντρης 6.3. Γωνία χορδής και εφαπτομένης 6.4. Βασικοί γεωμετρικοί τόποι στον κύκλο. 6.5 Το εγγεγραμμένο τετράπλευρο 6.6 Το εγγράψιμο τετράπλευρο (εκτός της απόδειξης του θεωρήματος)
|
Κεφάλαιο 1ο (Προτείνεται να διατεθούν 1 διδακτική ώρα) Κεφάλαιο 2ο Δεν θα διδαχθεί Κεφάλαιο 3ο (Προτείνεται να διατεθούν 19 διδακτικές ώρες) Κεφάλαιο 4ο (Προτείνεται να διατεθούν 10 διδακτικές ώρες) Κεφάλαιο 5ο (Προτείνεται να διατεθούν 17 διδακτικές ώρες) Κεφάλαιο 6ο (Προτείνεται να διατεθούν 3 διδακτικές ώρες)
ΣύνολαΣΥΝΟΛΑ: 50 ΩΡΕΣ ΕΒΔΟΜΑΔΕΣ: 25 ΜΗΝΕΣ ΚΑΤΑ ΠΡΟΣΕΓΓΙΣΗ: 6,5
|
| Περιεχόμενα - Σελίδες |
Διδακτέα ύλη 2014 - 2015 | Διαχείριση Διδακτέας ύλης |
|
|
Κεφ.3ο: Τρίγωνα 3.1 Είδη και στοιχεία τριγώνων 3.2 1ο Κριτήριο ισότητας τριγώνων (εκτός της απόδειξης του θεωρήματος) 3.3 2ο Κριτήριο ισότητας τριγώνων (εκτός της απόδειξης του θεωρήματος) 3.4 3ο Κριτήριο ισότητας τριγώνων (εκτός της απόδειξης του θεωρήματος) 3.5 Ύπαρξη και μοναδικότητα καθέτου (εκτός της απόδειξης του θεωρήματος) 3.6 Κριτήρια ισότητας ορθογώνιων τριγώνων(εκτός της απόδειξης των θεωρημάτων Ι και ΙΙ). 3.7 Κύκλος - Μεσοκάθετος ? Διχοτόμος 3.8 Κεντρική συμμετρία 3.9 Αξονική συμμετρία 3.10 Σχέση εξωτερικής και απέναντι γωνίας (εκτός της απόδειξης του θεωρήματος) 3.11 Ανισοτικές σχέσεις πλευρών και γωνιών(εκτός της απόδειξης του θεωρήματος) 3.12 Tριγωνική ανισότητα (εκτός της απόδειξης του θεωρήματος) 3.13 Κάθετες και πλάγιες (εκτός της απόδειξης του θεωρήματος II) 3.14 Σχετικές θέσεις ευθείας και κύκλου (εκτός της απόδειξης του θεωρήματος I) 3.15 Εφαπτόμενα τμήματα 3.16 Σχετικές θέσεις δύο κύκλων 3.17 Απλές γεωμετρικές κατασκευές 3.18 Βασικές κατασκευές τριγώνων Κεφ.4ο: Παράλληλες ευθείες 4.1. Εισαγωγή 4.2. Τέμνουσα δύο ευθειών - Ευκλείδειο αίτημα (εκτός της απόδειξης του Πορίσματος ΙΙ και των προτάσεων Ι , ΙΙ, ΙΙΙ και ΙV) 4.3. Κατασκευή παράλληλης ευθείας 4.4. Γωνίες με πλευρές παράλληλες 4.5. Αξιοσημείωτοι κύκλοι τριγώνου (εκτός της απόδειξης του θεωρήματος που αναφέρεται στον εγγεγραμμένο κύκλο τριγώνου). 4.6. Άθροισμα γωνιών τριγώνου 4.7. Γωνίες με πλευρές κάθετες (εκτός της απόδειξης του θεωρήματος και του πορίσματος) 4.8. Άθροισμα γωνιών κυρτού ν-γώνου (Εκτός της απόδειξης του Πορίσματος) Κεφ.5ο: Παραλληλόγραμμα - Τραπέζια 5.1. Εισαγωγή 5.2. Παραλληλόγραμμα 5.3. Ορθογώνιο 5.4. Ρόμβος 5.5. Τετράγωνο 5.6. Εφαρμογές στα τρίγωνα (εκτός της απόδειξης του Θεωρήματος ΙΙΙ) 5.7. Βαρύκεντρο τριγώνου (εκτός της απόδειξης του θεωρήματος) 5.8. Το ορθόκεντρο τριγώνου (Χωρίς το πόρισμα). 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου 5.10. Τραπέζιο 5.11. Ισοσκελές τραπέζιο 5.12. Αξιοσημείωτες ευθείες και κύκλοι τριγώνου Κεφ.6ο: Εγγεγραμμένα σχήματα 6.1. Εισαγωγικά ? Ορισμοί 6.2. Σχέση εγγεγραμμένης και αντίστοιχης επίκεντρης (Εκτός της απόδειξης του θεωρήματος) 6.3. Γωνία χορδής και εφαπτομένης (Εκτός της απόδειξης του θεωρήματος) 6.4. Βασικοί γεωμετρικοί τόποι στον κύκλο. 6.5 Το εγγεγραμμένο τετράπλευρο 6.6 Το εγγράψιμο τετράπλευρο (εκτός της απόδειξης του θεωρήματος)
|
Κεφάλαιο 1ο
(Προτείνεται να διατεθούν 15 διδακτικές ώρες) Κεφάλαιο 4ο (Προτείνεται να διατεθούν 8 διδακτικές ώρες) Κεφάλαιο 5ο (Προτείνεται να διατεθούν 20 διδακτικές ώρες) Κεφάλαιο 6ο (Προτείνεται να διατεθούν 6 διδακτικές ώρες)
ΣύνολαΣΥΝΟΛΑ: ΩΡΕΣ 50 ΕΒΔΟΜΑΔΕΣ: 25 ΜΗΝΕΣ ΚΑΤΑ ΠΡΟΣΕΓΓΙΣΗ: 6,5
|
Β' Λυκείου Άλγεβρα
- Details
- Category: catlykeio
- Published on 05 July 2014
- Written by Super User
- Hits: 284
Κατά το Σχολικό Έτος 2014 - 2015 η Άλγεβρα αποτελεί μάθημα γενικής παιδείας
και διδάσκεται τρείς (3) ώρες την εβδομάδα.
| Σχολικό Βιβλίο | Τίτλος Βιβλίου | Εβδομαδιαίες Ώρες Διδασκαλίας |
 |
Σχολικό έτος 2013 - 2014 Δύο (2) |
| Περιεχόμενα |
Διδακτέα ύλη 2013 - 2014 | Διαχείριση Διδακτέας ύλης |
|
ΚΕΦΑΛΑΙΟ 1ο : Συστήματα 1.1 Γραμμικά Συστήματα 1.2 Μη Γραμμικά Συστήματα ΚΕΦΑΛΑΙΟ 2ο : Ιδιότητες Συναρτήσεων 2.1 Μονοτονία-Ακρότατα-Συμμετρίες Συνάρτησης 2.2 Κατακόρυφη-Οριζόντια Μετατόπιση Καμπύλης ΚΕΦΑΛΑΙΟ 3ο : Τριγωνομετρία 3.1 Τριγωνομετρικοί Αριθμοί Γωνίας 3.2 Βασικές Τριγωνομετρικές Ταυτότητες 3.3 Αναγωγή στο 1O Τεταρτημόριο 3.4 Οι Τριγωνομετρικές Συναρτήσεις 3.5 Βασικές Τριγωνομετρικές Εξισώσεις 3.6 Τριγωνομετρικοί Αριθμοί Αθροίσματος Γωνιών 3.7 Τριγωνομετρικοί Αριθμοί της Γωνίας 2α 3.8 Μετασχηματισμοί Τριγωνομετρικών Παραστάσεων 3.9 Η Συνάρτηση f(x)=αημx+βσυνx 3.10 Επίλυση Τριγώνου ΚΕΦΑΛΑΙΟ 4ο : Πολυώνυμα-Πολυωνυμικές Εξισώσεις 4.1 Πολυώνυμα 4.2 Διαίρεση Πολυωνύμων 4.3 Πολυωνυμικές Εξισώσεις και Ανισώσεις 5.1 Εκθετική συνάρτηση 5.2 Λογάριθμοι 5.3 Λογαριθμική συνάρτηση |
1.1 Γραμμικά Συστήματα 1.2 Μη Γραμμικά Συστήματα Κεφ.2ο: Ιδιότητες Συναρτήσεων 2.1 Μονοτονία-Ακρότατα-Συμμετρίες Συνάρτησης 2.2 Κατακόρυφη-Οριζόντια Μετατόπιση Καμπύλης Κεφ. 3ο: Τριγωνομετρία 3.1. Τριγωνομετρικοί Αριθμοί Γωνίας 3.4 Οι τριγωνομετρικές συναρτήσεις Κεφ. 4ο: Πολυώνυμα - Πολυωνυ?ικές εξισώσεις 4.1. Πολυώνυμα Κεφ. 5ο: Εκθετική και Λογαριθμική συνάρτηση 5.1. Εκθετική συνάρτηση (να διδαχθούν μόνο οι λογαριθμικές συναρτήσεις με βάση το 10 και το e.). |
Κεφάλαιο 1ο (Προτείνεται να διατεθούν 6 διδακτικές ώρες) Κεφάλαιο 2ο (Προτείνεται να διατεθούν 3 διδακτικές ώρες) Κεφάλαιο 3ο (Προτείνεται να διατεθούν 16 διδακτικές ώρες) Κεφάλαιο 4ο (Προτείνεται να διατεθούν 15 διδακτικές ώρες) Κεφάλαιο 5ο (Προτείνεται να διατεθούν 10 διδακτικές ώρες) ΣύνολαΣΥΝΟΛΑ: 50 ΩΡΕΣ ΕΒΔΟΜΑΔΕΣ: 25 ΜΗΝΕΣ ΚΑΤΑ ΠΡΟΣΕΓΓΙΣΗ: 6,5
|
| Περιεχόμενα |
Διδακτέα ύλη 2014 - 2015 | Διαχείριση Διδακτέας ύλης |
|
ΚΕΦΑΛΑΙΟ 1ο : Συστήματα 1.1 Γραμμικά Συστήματα 1.2 Μη Γραμμικά Συστήματα ΚΕΦΑΛΑΙΟ 2ο : Ιδιότητες Συναρτήσεων 2.1 Μονοτονία-Ακρότατα-Συμμετρίες Συνάρτησης 2.2 Κατακόρυφη-Οριζόντια Μετατόπιση Καμπύλης ΚΕΦΑΛΑΙΟ 3ο : Τριγωνομετρία 3.1 Τριγωνομετρικοί Αριθμοί Γωνίας 3.2 Βασικές Τριγωνομετρικές Ταυτότητες 3.3 Αναγωγή στο 1O Τεταρτημόριο 3.4 Οι Τριγωνομετρικές Συναρτήσεις 3.5 Βασικές Τριγωνομετρικές Εξισώσεις 3.6 Τριγωνομετρικοί Αριθμοί Αθροίσματος Γωνιών 3.7 Τριγωνομετρικοί Αριθμοί της Γωνίας 2α 3.8 Μετασχηματισμοί Τριγωνομετρικών Παραστάσεων 3.9 Η Συνάρτηση f(x)=αημx+βσυνx 3.10 Επίλυση Τριγώνου ΚΕΦΑΛΑΙΟ 4ο : Πολυώνυμα-Πολυωνυμικές Εξισώσεις 4.1 Πολυώνυμα 4.2 Διαίρεση Πολυωνύμων 4.3 Πολυωνυμικές Εξισώσεις και Ανισώσεις 5.1 Εκθετική συνάρτηση 5.2 Λογάριθμοι 5.3 Λογαριθμική συνάρτηση |
Κεφ.1ο: Συστήματα 1.1 Γραμμικά Συστήματα ( χωρίς τις αποδείξεις των συμπερασμάτων της υποπαραγράφου « Λύση-Διερεύνηση γραμμικού συστήματος 2x2) Κεφ.2ο: Ιδιότητες Συναρτήσεων 2.1 Μονοτονία-Ακρότατα-Συμμετρίες Συνάρτησης Κεφ. 3ο: Τριγωνομετρία 3.1. Τριγωνομετρικοί Αριθμοί Γωνίας Κεφ. 4ο: Πολυώνυμα - Πολυωνυ?ικές εξισώσεις 4.1. Πολυώνυμα Κεφ. 5ο: Εκθετική και Λογαριθμική συνάρτηση 5.1. Εκθετική συνάρτηση |
Κεφάλαιο 1ο (Προτείνεται να διατεθούν 7 διδακτικές ώρες) Κεφάλαιο 2ο (Προτείνεται να διατεθούν 6 διδακτικές ώρες) Κεφάλαιο 3ο (Προτείνεται να διατεθούν 20 διδακτικές ώρες) Κεφάλαιο 4ο (Προτείνεται να διατεθούν 18 διδακτικές ώρες) Κεφάλαιο 5ο (Προτείνεται να διατεθούν 18 διδακτικές ώρες) ΣύνολαΣΥΝΟΛΑ: ΩΡΕΣ 69 ΕΒΔΟΜΑΔΕΣ: 23 ΜΗΝΕΣ ΚΑΤΑ ΠΡΟΣΕΓΓΙΣΗ: 6
|