

Για την προέλευση του προβλήματος υπάρχουν δύο σημαντικές μαρτυρίες.
Η πρώτη προέρχεται από τον Ευτόκιο , τον σχολιαστή του Αρχιμήδη, ο οποίος, δίχως να αναφέρει τις πηγές του, παραθέτει μια επιστολή του Ερατοσθένη προς τον βασιλιά Πτολεμαίο. Η έρευνα έχει αποδείξει ότι η επιστολή δεν είναι γνήσια, αλλά δεν υπάρχει λόγος να αμφιβάλλουμε ότι οι πληροφορίες που περιέχει είναι αξιόπιστες.
Η επιστολή αυτή αρχίζει ως εξής.
Λέγεται ότι κάποιος αρχαίος τραγωδοποιός εισήγαγε στη σκηνή τον Μίνωα, ο οποίος είχε διατάξει να κατασκευασθεί τάφος για τον γιο του Γλαύκο και όταν αυτός πληροφορήθηκε ότι ο τάφος ήταν σε όλες του τις διαστάσεις εκατό πόδια, είπε:
«Μικρή παράγγειλες τη χωρητικότητα του βασιλικού τάφου. Να διπλασιαστεί αυτή γρήγορα, αφού διπλασιαστεί κάθε πλευρά χωρίς, όμως, ο τάφος να χάσει το κομψό σχήμα του».
Φαινόταν δε ότι έκανε λάθος. Διότι, όταν διπλασιάζονται οι πλευρές, η μεν επιφάνεια τετραπλασιάζεται, ο δε όγκος οκταπλασιάζεται. Ζητήθηκε δε και από τους γεωμέτρες να βρουν, με ποιον τρόπο, ένα δεδομένο στερεό θα διπλασιαζόταν, χωρίς να χάνει το σχήμα του, και ονομαζόταν αυτό το πρόβλημα διπλασιασμός του κύβου. Διότι, υποθέτοντας ότι το δεδομένο στερεό ήταν κύβος, ζητούσαν να τον διπλασιάσουν. Ενώ δε όλοι επί πολύν χρόνο ήταν σε αμηχανία, πρώτος ο Ιπποκράτης ο Χίος επινόησε ότι αν βρεθούν δύο μέσες ανάλογοι σε συνεχή αναλογία, μεταξύ δύο ευθειών, εκ των οποίων η μία είναι διπλάσια της άλλης , τότε ο κύβος θα διπλασιαστεί. Αλλά με την επινόηση αυτή η αρχική αμηχανία περιέπεσε σε άλλη, όχι μικρότερη αμηχανία.
Λέγεται δε ακόμη ότι μετά πάροδο χρόνου μερικοί Δήλιοι, στους οποίους κάποιος χρησμός επέβαλε να διπλασιάσουν έναν από τους βωμούς τους, αφού περιέπεσαν στην ίδια αμηχανία, απέστειλαν εκπροσώπους και ζήτησαν από τους γεωμέτρες της Ακαδημίας του Πλάτωνα να λύσουν το πρόβλημα. Και αφού αυτοί επιδόθηκαν με ζήλο ζητώντας να κατασκευάσουν δύο μέσες αναλόγους μεταξύ δύο δεδομένων ευθειών, λέγεται ότι ο Αρχύτας ο Ταραντίνος έλυσε το πρόβλημα διά των ημικυλίνδρων και ο Εύδοξος διά των λεγομένων καμπύλων γραμμών.
Η δεύτερη μαρτυρία, προέρχεται από το Θέωνα το Σμυρναίο και βασίζεται σε ένα χαμένο διάλογο με τίτλο Πλατωνικός. Ένα απόσπασμα είναι το
Διότι στο βιβλίο του που επιγράφεται Πλατωνικός, ο Ερατοσθένης αφηγείται ότι , όταν ο θεός ανήγγειλε διά χρησμού στους Δηλίους ότι για να απαλλαγούν από τον λοιμό έπρεπε να κατασκευάσουν βωμό διπλάσιο του ήδη υπάρχοντος, οι αρχιτέκτονες περιέπεσαν σε μεγάλη αμηχανία ζητώντας με ποιον τρόπο μπορεί να διπλασιαστεί ένα στερεό και πήγαν να ρωτήσουν τον Πλάτωνα σχετικά με αυτό. Αυτός τους απάντησε ότι ο θεός έδωσε αυτόν τον χρησμό στους Δηλίους, όχι επειδή είχε ανάγκη ενός διπλάσιου βωμού, αλλά για να κατακρίνει και να επιπλήξει τους Έλληνες; επειδή αμελούν τα μαθηματικά και περιφρονούν τη γεωμετρία
Ο πρώτος γεωμέτρης ο οποίος ασχολήθηκε με το πρόβλημα, είναι ο Ιπποκράτης ο Χίος , ο οποίος απέδειξε ότι αν κατασκευάσουμε δύο τμήματα x και y ώστε να ισχύει :
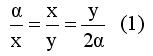
τότε το τμήμα x είναι το ζητούμενο. Πράγματι από τα δύο πρώτα κλάσματα της (1) προκύπτει αy = x
2
(2), και από το πρώτο και το τρίτο xy=2α
2
(3). Πολλαπλασιάζουμε την (3) με α και έχουμε xyα = 2α
3
και λόγω της (2) έχουμε
x
3
= 2α
3
Έτσι αν κατασκευάσουμε ένα κύβο με ακμή το τμήμα x , τότε ο όγκος του, που είναι ίσος με x 3 , θα είναι διπλάσιος του όγκου του κύβου με ακμή το τμήμα α.
Στη σχέση (1) στηρίζονται όλες οι λύσεις που δόθηκαν, όλοι οι γεωμέτρες προσπάθησαν να κατασκευάσουν τμήματα x και y , ώστε να ισχύει
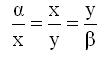
δηλ η (1) στην γενική της περίπτωση και στην προσπάθεια τους αυτή ανακάλυψαν σπουδαίες καμπύλες και μας κληροδότησαν ευφυείς λύσεις. Εμείς στις λύσεις που θα παρουσιάσουμε, για λόγους απλότητας, θα θεωρούμε αμέσως β=2α.
Κατά την ελληνική αρχαιότητα, δόθηκαν λύσεις στο πρόβλημα από: τον Αρχύτα τον Ταραντινό, τον Εύδοξο, τον Μέναιχμο, τον Πλάτωνα, τον Ερατοσθένη, τον Νικομήδη, τον Απολλώνιο, τον Ήρωνα, τον Φίλωνα τον Βυζάντιο, τον Διοκλή, τον Σπορο και τον Πάππο.