[ Home ] [ Up ]

ΤΟ SKETCHPAD KΑΙ ΤΟ ΑΓΑΛΜΑ

 Μπάμπης Τουμάσης

Δρ.Μαθηματικής Παιδείας

Νόρμαν 33, 26223, Πάτρα

 Στο άρθρο αυτό περιγράφουμε μια δραστηριότητα η οποία αναφέρεται στο σχολικό βιβλίο γεωμετρίας Β΄ Λυκείου. Ο βασικός μας σκοπός είναι να χρησιμοποιήσουμε ένα κλασικό πρακτικό πρόβλημα- το πρόβλημα του αγάλματος- στο πλαίσιο ενός δυναμικού λογισμικού περιβάλλοντος για να προσφέρουμε στους  μαθητές μια πλουσιότερη εμπειρία σχετικά με το τι είναι τα μαθηματικά και το τι σημαίνει να γνωρίζουμε και να κάνουμε μαθηματικά.

 

Ζούμε την εποχή της τεχνολογικής επανάστασης, την εποχή της έκρηξης της γνώσης και της πληροφορίας, όπου τα πάντα αλλάζουν με τρομακτικούς ρυθμούς, ακολουθώντας τους ξέφρενους ρυθμούς της επιστήμης. Σε ένα τέτοιο περιβάλλον τα σχολεία έχουν υποχρέωση να αλλάξουν ριζικά σε ανταπόκριση προς την ηλεκτρονική εποχή. Οι computers και τα άλλα υπολογιστικά μέσα γίνονται αργά αλλά σταθερά προεκτάσεις του μυαλού μας, αφού βιώνουμε όλο και πιο έντονα έναν κόσμο όπου οι μηχανές θα εκτελούν την περισσότερη πνευματική εργασία.

Πέρα απ’ αυτό, οι νέες τεχνολογίες στην εκπαίδευση και κυρίως οι computers και οι διάφορες υπολογιστικές μηχανές αλλάζουν τον τρόπο που δημιουργούνται τα μαθηματικά και επομένως είναι σε θέση να αλλάξουν ουσιωδώς τη φύση της μαθηματικής επιστήμης. Νέες τεχνικές, δομές, συμβολισμός και γλώσσα αναπτύσσονται συνεχώς και είναι φυσικό να δημιουργείται η ανάγκη να αναπτυχθούν νέα αντικείμενα, θεματικά πεδία και δραστηριότητες στα σχολικά προγράμματα ( Perkins et al., 1995).

Ειδικά το εκπαιδευτικό λογισμικό που έχει αναπτυχθεί στην περιοχή των μαθηματικών προσφέρει τη δυνατότητα στους μαθητές να προσεγγίσουν κάποιες ενότητες με μεγαλύτερη ευχέρεια, να επεξεργαστούν προβληματικές καταστάσεις με μεγαλύτερη ευκολία και να αισθητοποιήσουν αφηρημένες έννοιες μέσω πειστικών αναπαραστάσεων φαινομένων και καταστάσεων. Το γεγονός αυτό έχει σαν συνέπεια, αφενός μεν να δημιουργεί σημαντικές προοπτικές για εναλλακτικές προσεγγίσεις στη διδασκαλία των μαθηματικών και αφετέρου να βελτιώνει την εννοιολογική κατανόηση, καθώς επίσης και την ικανότητα επίλυσης προβλημάτων, όσο και τις στάσεις των μαθητών απέναντι στα μαθηματικά.

Τα τελευταία χρόνια έχει παγιωθεί στον εκπαιδευτικό κόσμο η αντίληψη της ενεργητικής μάθησης και της οικοδόμησης της γνώσης από το ίδιο το σκεπτόμενο άτομο. Ο μαθητής δεν μαθαίνει δεχόμενος παθητικά τις γνώσεις που του μεταδίδουν, αλλά αντίθετα αναδιοργανώνει ο ίδιος τις ενέργειές του, βοηθούμενος από το δάσκαλο, με στόχο να εξουδετερώσει τα εμπόδια που εμφανίζονται και να επεκτείνει την προγενέστερη γνώση , οικοδομώντας γέφυρες μεταξύ του παλιού και του νέου.

Ο ρόλος του δασκάλου αλλάζει, συνεπώς, ουσιωδώς. Από διανεμητής της γνώσης και εισηγητής, μετατρέπεται σε διευκολυντή της μαθησιακής διαδικασίας, επιδέξιο οργανωτή γόνιμων περιβαλλόντων μάθησης, μέσα από τα οποία καθοδηγεί διακριτικά τη νοητική δραστηριότητα των παιδιών και τα βοηθάει στo ξεδίπλωμα όλων των πτυχών της προσωπικότητας τους.

Την τελευταία δεκαετία έχουν κάνει την εμφάνισή τους αξιόλογα λογισμικά εκπαιδευτικά προγράμματα στο χώρο της Γεωμετρίας, όπως είναι τα Sketchpad (1995) και Cabri (1994).Tα εργαλεία αυτά επιτρέπουν την εξερεύνηση γεωμετρικών εννοιών και προβλημάτων με ένα δυναμικό τρόπο, προσφέροντας στους μαθητές τη δυνατότητα να μετατρέψουν τις στατικές έννοιες των σχολικών βιβλίων σε κινούμενα σχήματα, τα οποία συντίθενται και αποσυντίθενται. Η ικανότητα αυτή προσφέρει την εξαιρετική ευχέρεια να αναλύονται έννοιες και να μελετώνται προβλήματα, θεωρήματα και γενικά γεωμετρικές προτάσεις με παιδαγωγικά ισχυρούς τρόπους, που αλλιώς θα ήταν αδύνατο να πραγματοποιηθούν στο παραδοσιακό πλαίσιο του χαρτιού-και-μολυβιού. Τα λογισμικά αυτά συνδέουν οπτικές αναπαραστάσεις, διαπιστώσεις και εμπειρική σκέψη με υψηλότερα επίπεδα γεωμετρικής σκέψης, τα οποία περιλαμβάνουν δημιουργία συλλογισμών και τυπική απόδειξη (Batista & Clements, 1995).

Παρακάτω θα παρουσιάσουμε μια τέτοια ευκαιρία αξιοποίησης εκπαιδευτικού λογισμικού και συγκεκριμένα του Sketchpad στην εξερεύνηση ενός ιστορικού γεωμετρικού προβλήματος, το οποίο προτείνεται ως δραστηριότητα στο σχολικό βιβλίο Γεωμετρίας Α΄& Β΄ Λυκείου (Θωμαΐδης κ.α. 2000, 228).

Το πρόβλημα του αγάλματος

Το πρόβλημα αυτό, όπως αναφέρουν και οι συγγραφείς στο βιβλίο καθηγητή (Θωμαΐδης κ.α.,1999, 84) αποκαλείται και πρόβλημα του Ρεγκιομοντάνους. Ο Ρεγκιομοντάνους, ψευδώνυμο του Γερμανού μαθηματικού-αστρονόμου Johanes Müller, διατύπωσε το πρόβλημα αυτό γύρω στα 1471(Honsberger, 1970, 89). H διατύπωση του προβλήματος, όπως εμφανίζεται στην προτεινόμενη δραστηριότητα, είναι η εξής:

Υπάρχει ένα άγαλμα ύψους  α , το οποίο είναι στημένο πάνω σ’ ένα βάθρο ύψους  β . Ένας θεατής ύψους  υ , παρατηρεί το άγαλμα. Να βρεθεί η θέση του θεατή ώστε αυτός να βλέπει το άγαλμα με τη μεγαλύτερη δυνατή οπτική γωνία.

Το πρόβλημα θεωρείται αρκετά δύσκολο, γιατί απαιτεί τη σύνθεση πολλών γεωμετρικών εννοιών και γνώσεων, αλλά και τη μαθηματική μοντελοποίηση μιας μαθηματικής κατάστασης που συνθέτει ένα πρακτικό πρόβλημα. Απ’ αυτήν την άποψη, η αυστηρή-κλασική του αντιμετώπιση, όπως προτείνεται στο βιβλίο καθηγητή, είναι πολύ πέρα των δυνατοτήτων των μαθητών οι οποίοι παρακολουθούν ένα πρόγραμμα γενικής παιδείας. Αυτό τουλάχιστον διαβεβαιώνει η σχετική βιβλιογραφία, που αναφέρεται στις δυσκολίες και τα εμπόδια που συναντούν οι μαθητές στο γεωμετρικό-παραγωγικό συλλογισμό και στην τυπική αποδεικτική διαδικασία (Burger & Culpepper, 1993).

Ενώ όμως η φύση του προβλήματος και η απαίτηση για αυστηρή –τυπική επεξεργασία και διερεύνηση τo κάνει σχεδόν απροσπέλαστο για τους μαθητές της Β΄ Λυκείου, οι δυνατότητες που προσφέρει το λογισμικό πακέτο Sketchpad δίνουν την ευκαιρία για μια διαφορετική προσέγγιση και διερεύνησή του, η οποία προκαλεί και κινητοποιεί το ενδιαφέρον, αφού οι ιδέες που αναπτύσσονται με τα περιορισμένα εργαλεία των αρχαίων Ελλήνων παίρνουν τώρα σάρκα και οστά και ζωντανεύουν μπροστά στα μάτια των μαθητών με τη βοήθεια του computer.

Παρακάτω θα περιγράψουμε τα βασικά βήματα που συνθέτουν το σενάριο μιας τέτοιας προσέγγισης σ’ ένα δυναμικό γεωμετρικό περιβάλλον, η οποία ως κύριο στόχο έχει, αφενός μεν να δημιουργήσει τις προϋποθέσεις για μια ουσιαστική κατανόηση των ιδεών και εννοιών που συνθέτουν το παζλ που οδηγεί στη λύση αυτού του πρακτικού προβλήματος και αφετέρου να γεφυρώσει το χάσμα που υπάρχει σήμερα μεταξύ των δραστηριοτήτων που λαμβάνουν χώρα σ’ ένα σχολικό μάθημα γεωμετρίας και των εμπειριών του πραγματικού κόσμου.

 

Ένα διδακτικό σενάριο. 

 Οι μαθητές μπορούν να εργαστούν στην αίθουσα του εργαστηρίου Η/Υ του σχολείου, δουλεύοντας δύο-δύο μπροστά από κάθε υπολογιστή ή σε περίπτωση που δεν υπάρχει αυτή η δυνατότητα, να παρατηρούν τα βασικά βήματα της δραστηριότητας μέσω βίντεο-προβολέα και να απαντούν σε ερωτήματα που θα θέτει ο δάσκαλος των μαθηματικών.

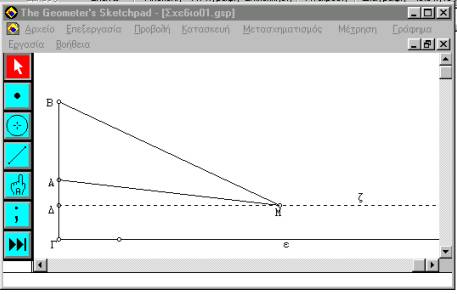
Αρχικά γίνεται προσπάθεια γεωμετρικής μοντελοποίησης του προβλήματος. Χρησιμοποιώντας τα εργαλεία κατασκευών του Sketchpad φτιάχνουμε το σχήμα 1, το οποίο θα χρησιμοποιήσουμε στη συνέχεια ως το γεωμετρικό μοντέλο του προβλήματος.

 Περίπτωση 1.          υ<β

                                        Σχήμα 1.

            Η ημιευθεία ε παριστάνει την ευθεία του εδάφους πάνω στην οποία

κινείται ο θεατής. Η διακεκομμένη ημιευθεία  ζ , παράλληλη της  ε , παριστάνει την ευθεία πάνω στην οποία κινείται το μάτι  Μ  του θεατή. Η ευθεία  ΓΒ , κάθετη στις  ε, ζ ,περιέχει το ευθύγραμμο τμήμα  ΑΒ , που παριστάνει το άγαλμα και το ευθύγραμμο τμήμα ΑΓ που παριστάνει το βάθρο του αγάλματος.

            Κατασκευάζουμε ένα σημείο  Μ πάνω στη  ζ , το οποίο μετακινείται και παριστάνει το μάτι του θεατή. Η γωνία , παριστάνει τη γωνία υπό την οποία ο θεατής βλέπει  κάθε φορά το άγαλμα. Ένα αρχείο εντολών για την κατασκευή του σχήματος 1, περιγράφεται στον πίνακα 1.

 


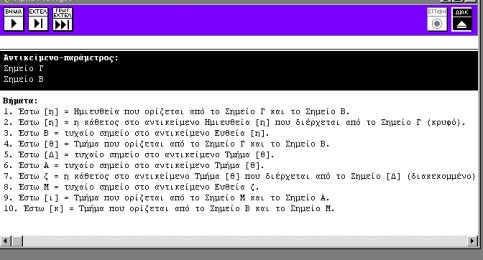
                              Πίνακας 1.

Αρχείο εντολών για την κατασκευή του σχήματος 1.

 

            Επιλέγουμε τις τρεις κορυφές Α,Μ,Β της γωνίας και από το μενού μέτρησης μετράμε τη γωνία. Καθώς μετακινούμε το σημείο Μ πάνω στην ημιευθεία  ζ , το Sketchpad εμφανίζει κάθε φορά και το μέτρο της γωνίας. Στον πίνακα 2 φαίνονται επτά  μετρήσεις γωνιών, όπως τις έχει πινακοποιήσει το ίδιο το Sketchpad.

            Οι μαθητές μπορούν εύκολα να παρατηρήσουν ότι υπάρχει μια θέση του Μ πάνω στη  ζ , όπου η γωνία γίνεται μέγιστη( 37,68ο στο παράδειγμα μας).

            Ο δάσκαλος ερωτά τους μαθητές τι το χαρακτηριστικό μπορεί να έχει αυτή η θέση του Μ. Αφού έχουμε γωνία η οποία «βλέπει» ένα ευθύγραμμο τμήμα, η σκέψη μας πηγαίνει στον κύκλο που ορίζεται κάθε φορά από τα τρία σημεία Α,Μ, Β. Γι’ αυτό κατασκευάζουμε τον κύκλο αυτόν. Επειδή το μενού «κατασκευή» δεν περιέχει κατασκευή κύκλου από τρία σημεία, κατασκευάζουμε τα τόξα και , οπότε εμφανίζεται ο κύκλος.

            Ο κύκλος αυτός φαίνεται πολύ καθαρά ότι πρέπει να εφάπτεται στην ευθεία  ζ. Για να το δούμε αυτό καλύτερα, μετακινούμε πάλι το σημείο Μ πάνω στην ευθεία  ζ, οπότε αλλάζει κάθε φορά και ο κύκλος. Τα σχήματα 3(α,β,γ) δείχνουν τρεις τέτοιες θέσεις του Μ με τον αντίστοιχο κάθε φορά περιγεγραμμένο κύκλο στο τρίγωνο ΜΑΒ.

                                                  Πίνακας 2.

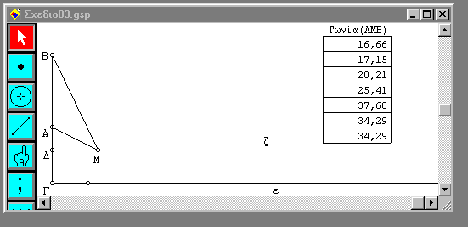
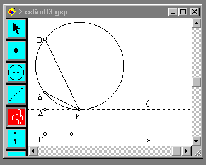
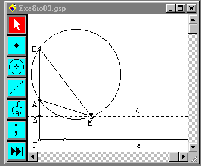
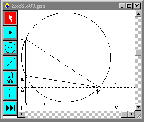
              Μετρήσεις της γωνίας για τις διάφορες θέσεις του Μ

                  (α)                                       (β)                                  (γ)     

                                                    Σχήμα 3.

           

            Στο σημείο αυτό ο δάσκαλος ζητάει από τους μαθητές να διατυπώσουν κάποια εικασία σχετικά με τη θέση του Μ η οποία μεγιστοποιεί τη γωνία .

Εικασία : Το σημείο το οποίο μεγιστοποιεί την γωνία , υπό την οποία ο θεατής βλέπει το άγαλμα ΑΒ, θα είναι το σημείο εκείνο Μ στο οποίο ο κύκλος που διέρχεται από τα Α, Β εφάπτεται στην ευθεία  ζ.

 

            Εδώ κάπου τελειώνει και η αποστολή του Sketchpad. To εργαλείο αυτό βοήθησε στην εξερεύνηση του προβλήματος μέχρι τη διατύπωση της εικασίας, της πρότασης, δηλαδή η οποία θα πρέπει να ελεγχθεί και ή να αποδειχθεί ή να απορριφθεί.

            Στο σημείο αυτό ο δάσκαλος προτρέπει τους μαθητές να εκτυπώσουν το σχήμα 3(α) με τον εφαπτόμενο κύκλο και να εργαστούν από δω και πέρα στο χαρτί, με το μολύβι και τα γεωμετρικά τους όργανα, προσπαθώντας να αποδείξουν την εικασία, διατυπώνοντας τα επιχειρήματα και τους συλλογισμούς τους.

            Η απόδειξη θα πρέπει να είναι αφενός μεν χαλαρή, έτσι ώστε να ταιριάζει στο επίπεδο διανοητικής ωριμότητας των μαθητών και αφετέρου πειστική. Αυτό επιτυγχάνεται με την παράβλεψη της περίπτωσης του κύκλου που διέρχεται από τα Α,Β και τέμνει την ευθεία  ζ , έτσι ώστε η προσπάθεια να επικεντρωθεί στην περίπτωση του εφαπτόμενου κύκλου. Οι μαθητές αρκεί, από παιδαγωγικής απόψεως, να δείξουν ότι εάν Μ1 είναι μια οποιαδήποτε άλλη θέση του ματιού του θεατή τότε < (σχήμ.4)

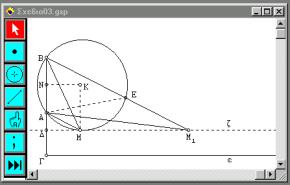Ο δάσκαλος υποδεικνύει στους μαθητές να συγκρίνουν τις γωνίες

,και, οπότε εύκολα διαπιστώνεται ότι.

Το ερώτημα που φυσιολογικά εγείρεται στη συνέχεια είναι με ποιο τρόπο θα κατασκευαστεί ο εφαπτόμενος κύκλος.                                               Σχήμα 4.

            Η λύση που προτείνουν οι συγγραφείς στο βιβλίο καθηγητή βασίζεται στην έννοια της δύναμης σημείου ως προς κύκλο, καθώς και στην έννοια της μέσης αναλόγου, μια κατασκευή, δηλαδή, αρκετά πολύπλοκη για μαθητές γενικής παιδείας. Γι’ αυτό εμείς θα προτείνουμε την πολύ απλούστερη λύση που έδωσε ο μαθηματικός  Α. Lorsch και αναφέρεται στο βιβλίο του H. Dörrie(1965, 369) «100 μεγάλα προβλήματα των στοιχειωδών μαθηματικών».

            Ο δάσκαλος, μέσα από συζήτηση, βοηθάει τους μαθητές να παρατηρήσουν ότι το κέντρο Κ του ζητούμενου κύκλου θα πρέπει :

(α) Να ισαπέχει από τα Α και Β και επομένως να βρίσκεται στη μεσοκάθετο της ΑΒ.

(β) Να απέχει από την ευθεία ζ απόσταση ΜΚ=ΑΚ=ΒΚ=ΝΔ, όπου Ν το μέσο του ΑΒ.

Επομένως το Κ θα είναι το σημείο τομής της μεσοκαθέτου ΝΚ και του κύκλου κέντρου Α ή Β και ακτίνας ΝΔ, που είναι δεδομένη και σταθερή.

            Η δραστηριότητα όμως συνεχίζεται, αφού το πρόβλημα πρέπει να διερευνηθεί και στις άλλες δύο περιπτώσεις:

 

Περίπτωση 2 :   β

               

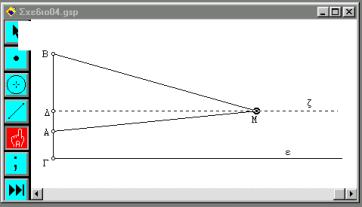
            Πάλι με τη βοήθεια των εργαλείων του Sketchpad κατασκευάζουμε το γεωμετρικό μοντέλο του προβλήματος, όπως φαίνεται στο σχήμα 5.

                                               Σχήμα 5

            Μετράμε τη γωνία και βλέπουμε τις μετρήσεις καθώς μετακινούμε το σημείο Μ πάνω στην ημιευθεία  ζ. Παρατηρούμε ότι όχι μόνο δεν υπάρχει κάποια θέση του σημείου Μ στην οποία η γωνία

να γίνεται μεγίστη, αλλά απεναντίας το μέτρο της αυξάνει συνέχεια, καθώς το Μ προσεγγίζει το Δ, τείνοντας στις 180ο. Στο σχήμα 6 φαίνονται τα πινακοποιημένα αποτελέσματα των μετρήσεων για οκτώ θέσεις του σημείου Μ.

            Διατυπώνεται λοιπόν η εικασία : όταν  δεν υπάρχει μέγιστη γωνία, αλλά όσο πιο κοντά πλησιάζουμε στο άγαλμα τόσο καλύτερα το βλέπουμε.

            Εκτυπώνεται πάλι το σχήμα 5 και ο δάσκαλος προτρέπει τους μαθητές να δουλέψουν με τα γεωμετρικά τους όργανα πάνω στο χαρτί για να αποδείξουν την εικασία.

            Στο σχήμα, η γωνίαείναι το άθροισμα των γωνιών και. Αυτή η παρατήρηση βοηθάει πολύ στην απόδειξη, αφού εύκολα γίνεται αντιληπτό ότι καθώς το Μ πλησιάζει το Δ και οι δύο αυτές γωνίες τείνουν να γίνουν 90ο

.

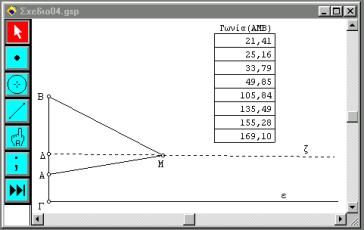
                                                Σχήμα 6

 

Περίπτωση 3 :      υ > α+β

            Η περίπτωση αυτή αντιμετωπίζεται όπως ακριβώς και η πρώτη περίπτωση (σχήμα  7).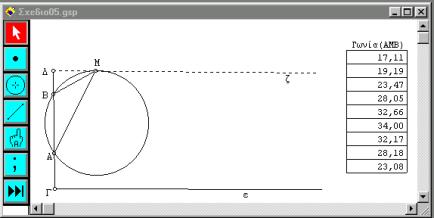

                                                 Σχήμα 7

 Στο σχήμα αυτό φαίνονται εννέα θέσεις του σημείου Μ με τις μετρήσεις της γωνίας , όπου η μέγιστη γωνία(34ο) επιτυγχάνεται όταν το Μ είναι το σημείο επαφής του κύκλου που διέρχεται από τα Α,Β και εφάπτεται στην ημιευθεία  ζ.

 

Συμπερασματικά.

             Η εισαγωγή νέων τεχνολογιών στη διδασκαλία των μαθηματικών, μολονότι περικλείει αρκετές παγίδες (Kaput, 1992), σε ορισμένες περιπτώσεις αποδεικνύεται ισχυρό εργαλείο διερεύνησης και κατανόησης μαθηματικών εννοιών. Στο συγκεκριμένο παράδειγμα που περιγράψαμε παραπάνω, φαίνεται η παιδαγωγική αξία του δυναμικού γεωμετρικού περιβάλλοντος που αναπτύχθηκε με τη βοήθεια του Sketchpad και η δυνατότητα αλλαγής του τρόπου με τον οποίο οι μαθητές μπορούν να προσεγγίσουν παραδοσιακές μαθηματικές ιδέες και να μοντελοποιούν πρακτικά προβλήματα.

            Οι ευκαιρίες για πειραματισμό, εξερεύνηση, διερεύνηση περιπτώσεων, δημιουργία εικασιών, ελέγχου αυτών, αναθεώρησής τους ή τελικής τους απόδειξης, συνιστούν την πεμπτουσία της μαθηματικής δημιουργίας και του μαθηματικού γίγνεσθαι. Προσφέρουν δε σε όλους τους μαθητές τη δυνατότητα να συζητήσουν μαθηματικές ιδέες και να αισθανθούν την ανάγκη να δικαιολογήσουν με συλλογισμούς τις απόψεις τους πέραν «του τι μας λέει ο υπολογιστής ότι φαίνεται να ισχύει».

            Ο βασικός στόχος παρόμοιων δραστηριοτήτων είναι να αξιοποιηθούν κλασικά μαθηματικά προβλήματα, θεωρήματα ή προτάσεις σε συνδυασμό με εκπαιδευτικό λογισμικό, έτσι ώστε να προσφέρουν στους μαθητές πλουσιότερες εμπειρίες γύρω από το τι είναι τα μαθηματικά και το τι σημαίνει να γνωρίζουμε και να κάνουμε μαθηματικά.

 ΒΙΒΛΙΟΓΡΑΦΙΚΕΣ   ΑΝΑΦΟΡΕΣ

 Batista, M.&Douglas,C.(1995). “Connecting Research to Teaching: Geometry and Proof”. Mathematics Teacher, 88, 48-54.

Baulac,Y.,Bellemain,F. and Laborde,J.(Designers),(1994). Dallas, Tex. : Texas Instruments,Software.

Burger,W.& Culpepper,B.(1993). “Restructuring Geometry”. In Patricia, W.(Ed.), Research ideas for the Classroom-High school Mathematics. National Council of Teachers of Mathematics.

Dörrie,H.(1965). “100 Great Problems of Elementary Mathematics”. New York: Dover Publications.

Honsberger,R.(1970). “ Ingenuity in Mathematics”. The Mathematical Association of America.

Θωμαΐδη,Γ. κ.α(1999). «Ευκλείδεια Γεωμετρία. Βιβλίο του καθηγητή», ΟΕΔΒ.

Θωμαΐδη,Γ. κ.α(2000). «Ευκλείδεια Γεωμετρία Α΄ και Β΄ Λυκείου», ΟΕΔΒ.

Kaput,J.(1986). “Technology and Mathematics Education”. In Grouws,D.(Ed), Handbook of Research on Mathematics Teaching and Learning. New York: Macmillan International.

Patricia,W.(Ed.)(1993). “Research Ideas for the Classroom-High School Mathematics” .National Council of Teachers of Mathematics.

Perkins,D. et al.(eds)(1995). “ Software goes to school : Teaching for understanding with new Technology”. New York: Oxford University Press.

Jackiw,N.(designer)(2000). “The Geometer’s Sketchpad.”. Berkeley, Calif.: Key Curriculum Press. Software(Ελληνική Έκδοση).

 

ABSTRACT

 

            In this article we describe an activity which was drawn from a school geometry textbook. Our main goal was to use a classic real situation problem-the statue problem- in the context of a dynamic software environment to connect students to a richer experience of what mathematics is and what it means to know and do mathematics.