[ Home ] [ Up ]

ΤΟ ΠΡΟΒΛΗΜΑ ΤΗΣ ΓΚΑΡΑΖΟΠΟΡΤΑΣ: ΜΙΑ

ΔΡΑΣΤΗΡΙΟΤΗΤΑ ΣΕ ΠΕΡΙΒΑΛΛΟΝ

ΔΥΝΑΜΙΚΗΣ ΓΕΩΜΕΤΡΙΑΣ

Περίληψη

Ένας βασικός σκοπός της διδασκαλίας και μάθησης των μαθηματικών είναι η ανάπτυξη του μαθηματικού δυναμικού όλων των μαθητών. Για την εκπλήρωση αυτού του σκοπού οι δάσκαλοι πρέπει να επιλέγουν ενδιαφέροντα και προκλητικά μαθηματικά προβλήματα, να προάγουν τη διερεύνηση των μαθηματικών ιδεών και να αξιοποιούν την τεχνολογία. Στην εργασία αυτή παρουσιάζουμε μια προβληματική κατάσταση, η οποία αναλύεται σε ένα δυναμικό γεωμετρικό περιβάλλον και προσφέρει στους μαθητές μια πλούσια εμπειρία σχετικά με το «τι είναι μαθηματικά και τι σημαίνει να γνωρίζουμε και να κάνουμε μαθηματικά».

Εισαγωγή

Ένας από τους βασικούς σκοπούς της μαθηματικής εκπαίδευσης είναι η ανάπτυξη και καλλιέργεια των μαθηματικών ικανοτήτων όλων των μαθητών. Ο ρόλος του δασκάλου των μαθηματικών είναι καθοριστικός στην εκπλήρωση αυτού του σκοπού, λαμβανομένου μάλιστα υπόψη ότι ο αφαιρετικός χαρακτήρας και η αυστηρότητα στη δομή των μαθηματικών κάνουν τη διδασκαλία και την κατανόησή τους αρκετά δύσκολη υπόθεση (Hirschhorn & Thompson, 1996). Κάποιες διδακτικές ενέργειες τις οποίες θα μπορούσαν να υιοθετήσουν οι δάσκαλοι για την εκπλήρωση του παραπάνω σκοπού είναι: (NCTM, 1991,1)

•  Επιλογή προβληματικών καταστάσεων οι οποίες θα προκαλούσαν το ενδιαφέρον και την περιέργεια των μαθητών.
•  Δημιουργία ευκαιριών οι οποίες θα βοηθούσαν τους μαθητές να διευρύνουν την κατανόηση των μαθηματικών και των εφαρμογών τους.
•  Προώθηση της εξερεύνησης των μαθηματικών ιδεών.
•  Χρήση της τεχνολογίας για την πραγματοποίηση αυτής της εξερεύνησης.
•  Ανακάλυψη διασυνδέσεων με τις προηγούμενες μαθηματικές γνώσεις.
•  Αξιοποίηση συνεργατικών μεθόδων μάθησης.

Επιλογή προβληματικών καταστάσεων

Αρκετοί δάσκαλοι των μαθηματικών καταβάλουν φιλότιμες προσπάθειες προκειμένου να βρουν εποικοδομητικούς τρόπους να εκπληρώσουν τις παραπάνω διδακτικές ενέργειες μέσω δημιουργικών δραστηριοτήτων. Στην προσπάθειά τους όμως αυτή συναντούν πολλά εμπόδια, τα οποία πηγάζουν κυρίως από το γεγονός ότι τα σχολικά βιβλία δεν αντανακλούν το παραπάνω πνεύμα, ενώ τα αναλυτικά προγράμματα είναι πάρα πολύ εκτεταμένα, σε αντίθεση με τον περιορισμένο διδακτικό χρόνο, έτσι ώστε να μην επιτρέπoυν την εξερεύνηση, τον πειραματισμό και τις εναλλακτικές μαθησιακές εμπειρίες.

Έχουμε όμως την εντύπωση ότι η επιλογή κατάλληλων προβληματικών καταστάσεων και η παρουσίασή τους στην τάξη, σε τακτά έστω χρονικά διαστήματα, μπορεί να σπάσει τη ρουτίνα της καθημερινής διδακτικής πράξης και να προσφέρει στους μαθητές τη δυνατότητα να πάρουν μια γεύση από τη μαγεία της μαθηματικής δημιουργίας και ανακάλυψης.

Τα μαθηματικά προβλήματα που περιέχονται στα σχολικά βιβλία μαθηματικών είναι κατά κανόνα θεωρητικού χαρακτήρα, εφαρμογές μιας συγκεκριμένης θεωρίας και συνήθως αποκομμένα από την πραγματικότητα. Οι δραστηριότητες επίσης που παρουσιάζονται είναι αποκομμένες από το επιστημονικό-ιστορικό πλαίσιο αναφοράς τους με προφανή αρνητικό αντίκτυπο στις σύγχρονες διαδικασίες έρευνας, πειραματισμού, ανάπτυξης εικασιών και επίλυσης προβλημάτων.

Το κακό συνεχίζεται με τη διδασκαλία να βασίζεται στις εντολές και συνταγές του δασκάλου, ο οποίος αποκαλύπτει τα κρίσιμα σημεία του προβλήματος αντί να προκαλέσει την περιέργεια των μαθητών, έτσι ώστε με κατάλληλη υποστήριξη να επινοηθούν από τους ίδιους.

Καλό μαθηματικό πρόβλημα είναι αυτό που όχι μόνο προκαλεί το ενδιαφέρον των μαθητών, αλλά προσφέρει ευκαιρίες για πειραματισμό, εξερεύνηση και γενικά δημιουργική δράση. Είναι ανάγκη να μετατοπιστεί η έμφαση από την επικρατούσα αντίληψη ότι «Εδώ υπάρχει ένα πρόβλημα και λύσε το», στην άποψη ότι «Εδώ υπάρχει μια προβληματική κατάσταση, ας τη διερευνήσουμε».

Ορισμένα χαρακτηριστικά τα οποία πιστεύουμε ότι θα πρέπει να αναζητήσει ο δάσκαλος των μαθηματικών στην προσπάθειά του να επιλέξει μια προβληματική κατάσταση είναι τα παρακάτω:

•  Το πλαίσιο αναφοράς της προβληματικής κατάστασης να αναφέρεται σε έναν οικείο τομέα ή να συνδέεται με φυσικά φαινόμενα, έτσι ώστε να έχει κάποιο νόημα για τους μαθητές.
•  Τα ερωτήματα του προβλήματος, αφενός μεν να μην οδηγούν σε προφανείς απαντήσεις και αφετέρου να μην είναι πολύ μεγάλης δυσκολίας ή να απαιτούν εξεζητημένες γνώσεις και τεχνικές πέρα των δυνατοτήτων των μαθητών.
•  Η δομή του προβλήματος πρέπει να είναι τέτοια ώστε να προσφέρει ευκαιρίες και για πειραματισμό, αναζήτηση, επινόηση, δημιουργία εικασιών, συζήτηση και ανταλλαγή απόψεων και συνεργατική μάθηση.
•  Τα ερωτήματα του προβλήματος, καλό θα είναι να είναι διατυπωμένα με ανοικτή αντίληψη και με τέτοιο τρόπο ώστε να μπορούν να διερευνηθούν σε διαφορετικά επίπεδα κατανόησης.

Ο ρόλος του δασκάλου έχει μεγάλη σημασία, επίσης, για την επιτυχή ολοκλήρωση μιας δραστηριότητας μέσα στην τάξη. Ο δάσκαλος είναι υπεύθυνος για τη δημιουργία κλίματος αναζήτησης, προβληματισμού, καθώς επίσης και κατάλληλων πλαισίων δράσης, έτσι ώστε οι μαθητές να διευκολύνονται στην αναζήτηση, την παρατήρηση, τη μαθηματικοποίηση και τελικά στην κατανόηση του προβλήματος. Για το σκοπό αυτό ο δάσκαλος γίνεται ο ίδιος συνερευνητής, καθοδηγώντας διακριτικά τους μαθητές και προσφέροντάς τους κάθε φορά το απαιτούμενο ποσό πληροφορίας ή τη ελάχιστη δυνατή βοήθεια προκειμένου να εντοπιστούν κρίσιμα σημεία ή να ξεπεραστούν δυσκολίες (kanold, 1990).

Στη συνέχεια θα παρουσιάσουμε ένα πρόβλημα-δραστηριότητα, το οποίο πιστεύουμε ότι πληροί σε ικανοποιητικό βαθμό τις παραπάνω προδιαγραφές και θα προσπαθήσουμε να αναλύσουμε τη διδακτική μας πρόταση για τη διαπραγμάτευσή του σε ένα περιβάλλον δυναμικής γεωμετρίας.

Το εκπαιδευτικό λογισμικό που έχει αναπτυχθεί στην περιοχή των μαθηματικών τα τελευταία δέκα χρόνια προσφέρει τη δυνατότητα κατασκευής κατάλληλων μικρόκοσμων διερεύνησης, καθώς επίσης και εφαρμογής εναλλακτικών διδακτικών προσεγγίσεων. Οι μαθητές έχουν τη δυνατότητα να προσεγγίσουν κάποιες ενότητες με μεγαλύτερη ευχέρεια, να αισθητοποιήσουν αφηρημένες έννοιες μέσω πειστικών αναπαραστάσεων, να διαισθανθούν την κίνηση, να πειραματιστούν, να αναπτύξουν υποθέσεις και να ελέγξουν εικασίες (Αρβανίτης & Τουμάσης, 2003).

Διατύπωση του προβλήματος

Το παρακάτω πρόβλημα αποτελεί παραλλαγή μιας δραστηριότητας που παρουσιάζεται στο βιβλίο του Brian Bolt «Τα Μαθηματικά συναντούν την Τεχνολογία» και αναφέρεται από τους Oldknow & Taylor(2003, 236).

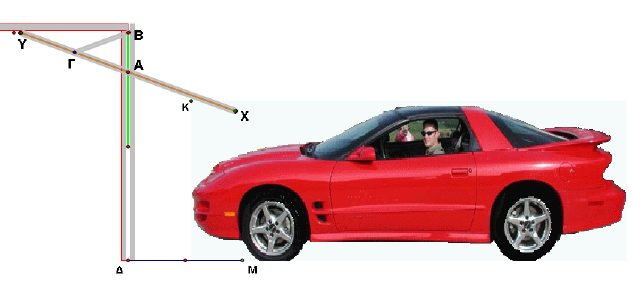
Το πρόβλημα της γκαραζόπορτας

εικόνα 1

Η παραπάνω εικόνα 1 απεικονίζει μια γκαραζόπορτα με τα εξής χαρακτηριστικά:

• Η πόρτα ΧΥ έχει μήκος 2m και ΑΓ=ΓΥ=ΓΒ=0,5m.
• Η πόρτα ανοίγει απ’ έξω τραβώντας το άκρο της Χ προς τα έξω και προς τα πάνω.
• Μια περόνη Α στην πόρτα ολισθαίνει κατά μήκος μιας κάθετης ράβδωσης στον ξύλινο στύλο ΒΔ, ενώ το σημείο Γ είναι κατασκευασμένο να περιστρέφεται γύρω από το Β με τη βοήθεια της ράβδου ΒΓ.
• Υποθέτουμε ότι το κατακόρυφο εμπρόσθιο μέρος του αυτοκινήτου έχει μήκος α=0,58m από το έδαφος.

1. Ποια θα είναι η διαδρομή του σημείου Γ καθώς η πόρτα ανοιγοκλείνει;
2. Ποια θα είναι η διαδρομή του σημείου Υ καθώς η πόρτα ανοιγοκλείνει;
3. Ποια θα είναι η διαδρομή του σημείου Χ καθώς η πόρτα ανοιγοκλείνει;
4. Ποια θα είναι η ελάχιστη απόσταση από το σημείο Δ που ο οδηγός θα πρέπει να σταματήσει το αυτοκίνητο για να μπορέσει να ανοίξει την πόρτα;
5. Ποιο θα πρέπει να είναι το σχήμα του μπροστινού και του πίσω μέρους του αυτοκινήτου προκειμένου να διευκολύνεται η είσοδος και η έξοδός του;

Η διερεύνηση του παραπάνω προβλήματος είναι δυνατόν να γίνει σε δύο επίπεδα κατανόησης. Στο πρώτο επίπεδο, για μαθητές Γυμνασίου, η επεξεργασία του προβλήματος μπορεί να γίνει με πρακτικό-εμπειρικό τρόπο μέσω της αξιοποίησης των εργαλείων και των υπολογιστικών δυνατοτήτων του δυναμικού γεωμετρικού λογισμικού, με συστηματική παρατήρηση και μέτρηση. Στο δεύτερο επίπεδο, για μαθητές Λυκείου, μπορούμε να έχουμε μια πιο ολοκληρωμένη προσέγγιση. Οι μαθητές, δηλαδή, αφού μαντέψουν με τη βοήθεια των εργαλείων του λογισμικού τις απαντήσεις στις ερωτήσεις του προβλήματος, στη συνέχεια με την καθοδήγηση του δασκάλου μπορούν να κατασκευάσουν και τις ανάλογες αποδείξεις. Ένα από τα ζητούμενα στη δεύτερη αυτή περίπτωση είναι ο μαθητής να μάθει να χειρίζεται με ευχέρεια το μαθηματικό συμβολισμό και τις προγενέστερες γνώσεις, προκειμένου να δημιουργεί συλλογισμούς και να συνθέτει μαθηματικές αποδείξεις, οι οποίες θα πιστοποιούν τα συμπεράσματα των παρατηρήσεων του.

Αποτύπωση του προβλήματος σε περιβάλλον δυναμικής γεωμετρίας.

Στη φάση αυτή καταβάλλεται προσπάθεια να δημιουργηθεί ένα γεωμετρικό μοντέλο, το οποίο θα περιγράφει το μηχανισμό κίνησης της γκαραζόπορτας και θα αναπαριστά τα δεδομένα και κυρίως την κίνηση του μηχανισμού της πόρτας και του αυτοκινήτου. Επειδή ο μηχανισμός κίνησης της πόρτας είναι πολύπλοκος και απαιτεί μεγάλη εξοικείωση με τις δυνατότητες ενός δυναμικού γεωμετρικού λογισμικού όπως το Sketchpad και το Cabri, προτείνουμε να δημιουργηθεί το βασικό μοντέλο προσομοίωσης του προβλήματος από το δάσκαλο και να αποτελέσει ένα έτοιμο αρχείο, το οποίο θα χειριστούν αργότερα δυναμικά οι μαθητές προκειμένου να πειραματιστούν.

Παρακάτω περιγράφουμε τα σημαντικότερα στοιχεία κατασκευής ενός τέτοιου αρχείου με το λογισμικό Sketchpad, 4.2, όπως φαίνεται στην εικόνα 2.

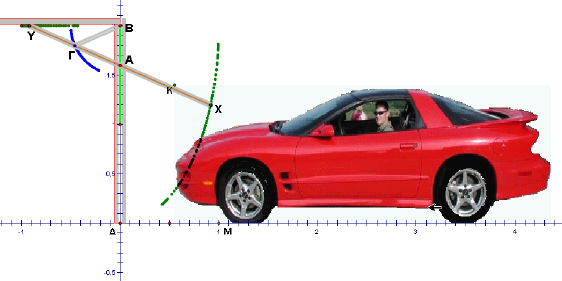
εικόνα 2

Σε ορθογώνιο σύστημα συντεταγμένων θεωρούμε κλίμακα αντιστοίχησης 1μονάδα του συστήματος = 1m. Ορίζουμε σταθερό σημείο Β(0,2) , σταθερό σημείο Ε(0,1) , το μέσον δηλαδή του τμήματος ΒΔ και το τμήμα ΕΒ. Πάνω στο ΕΒ σχεδιάζουμε κινητό σημείο Α, το οποίο αντιστοιχεί στην κινητή περόνη που κινείται πάνω στην κατακόρυφη αυλακωτή δοκό της πόρτας. Σχεδιάζουμε τους κύκλους C(Α,1 m) , F(A, 0,5 m) και L(B, 0,5 m). Οι κύκλοι F και L τέμνονται σε δύο σημεία, ένα από τα οποία είναι το σημείο Γ. Η ευθεία ΑΓ ορίζει κάθε φορά την θέση της γκαραζόπορτας, και αφού η πόρτα θα είναι 2 m, το μήκος και η θέση της θα ορίζονται από την διάμετρο ΥΓΑΧ του κύκλου C.

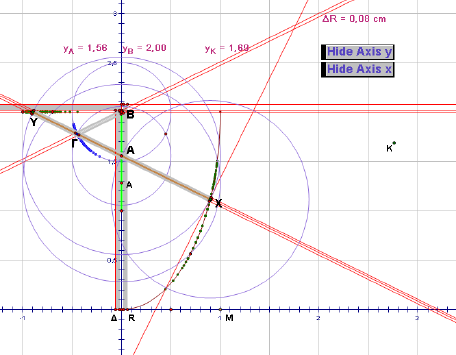
εικόνα 3

Στην εικόνα 3 βλέπουμε μια άποψη του αρχείου κατά την διάρκεια κατασκευής πριν αποκρύψουμε τα περιττά στοιχεία.

Επειδή η πλήρης περιγραφή της κατασκευής του αρχείου δεν είναι εφικτή στην παρούσα εργασία (θα χρειάζονταν 3 ή 4 σελίδες επιπλέον κείμενο και εικόνες), οι ενδιαφερόμενοι μπορούν να το κατεβάσουν (Downloand) από τον σύνδεσμο Το πρόβλημα της γκαραζόπορτας.

Πειραματισμός-δημιουργία εικασιών.

Αρχικά, ενθαρρύνουμε τους μαθητές να χειριστούν δυναμικά το σημείο Χ, προκειμένου να θέσουν σε κίνηση το μηχανισμό της πόρτας και να μαντέψουν την τροχιά των σημείων Υ και Γ. Αφού οι μαθητές διατυπώσουν τις εικασίες τους για τις τροχιές των σημείων Υ, Γ και Χ, γίνεται η σχετική συζήτηση μέσα στην τάξη για ανταλλαγή και αντιπαράθεση απόψεων.

Στη συνέχεια με την ενεργοποίηση της εντολής του Sketchpad «Σχεδίαση ίχνους» γίνεται δυνατή η αποτύπωση των τροχιών των σημείων και επιβεβαιώνονται ή απορρίπτονται και ανασκευάζονται οι αρχικές προβλέψεις.

Τελικά διατυπώνονται οι παρακάτω ισχυρισμοί- εικασίες:

1. Το σημείο Υ κινείται σε μια ημιευθεία κάθετη στη δοκό ΒΔ στο σημείο Β.
2. Το σημείο Γ κινείται σε ένα κύκλο με κέντρο το σταθερό σημείο Β.
3. Το σημείο Χ κινείται σε μια καμπύλη που μοιάζει με το ένα τέταρτο έλλειψης, της οποίας οι εστίες βρίσκονται πάνω και στην προέκταση της δοκού ΔΒ.

εικόνα 4

Προκειμένου να απαντήσουν οι μαθητές στο ερώτημα 4 του προβλήματος, τους προτρέπουμε να χειριστούν δυναμικά την εικόνα του αυτοκινήτου σύροντας με το ποντίκι το σημείο Κ στο πάνω αριστερό μέρος της εικόνας 5.

εικόνα 5

Το σενάριο μπορεί να είναι όπως παρακάτω:

Υποθέτουμε ότι 1 μονάδα στο σύστημα συντεταγμένων αντιστοιχεί σε 1 m μήκος, τότε για το συγκεκριμένο αυτοκίνητο της εικόνας του οποίου το εμπρόσθιο τμήμα έχει ύψος 0,58 m, κάντε τα εξής:

• Εμφανίστε τους άξονες.
• Σύρατε το σημείο Χ για να δείτε την τροχιά του.
• Μετρήστε την τετμημένη του σημείου Κ (αυτή ορίζει την απόσταση του αυτοκινήτου από την πόρτα, αφού βρίσκεται στην κατακόρυφο που περνάει από το εμπρόσθιο σημείο του αυτοκινήτου). Αφού επιλέξετε το σημείο Κ, από το μενού Measure κάντε κλικ στην εντολή Abscissa(χ)
• Όμοια επιλέξτε το σημείο X και σύρατε το έως ότου πλησιάσει το μπροστινό μέρος του αυτοκινήτου. Αν το αυτοκίνητο δεν είναι αρκετά κοντά επιλέξτε το και σύρατε το προς τον τοίχο. Μετρήστε την τεταγμένη του (αυτή ορίζει το ύψος του μπροστινού τμήματος). Από το μενού Measure κάντε κλικ στην εντολή Ordinate(y)
• Ο άξονας χ΄χ είναι ο δρόμος. Πόσο κοντά στον τοίχο πρέπει να φτάσει το αυτοκίνητο για να μπορεί να ανοίξει η πόρτα;

Τελικά διατυπώνεται το συμπέρασμα που προκύπτει από την παρατήρηση: Ο οδηγός πρέπει να σταματήσει το αυτοκίνητο σε απόσταση τουλάχιστον 0,70 μέτρα από την είσοδο Δ της πόρτας.

Η απάντηση στο ερώτημα 5 είναι τώρα εύκολη υπόθεση για τους μαθητές, αφού διευκολύνεται από την εποπτεία που προσφέρει ο δυναμικός χειρισμός του σχήματος. Λόγω της ελλειπτικής τροχιάς του άκρου Χ, θα πρέπει το μπροστινό μέρος του αυτοκινήτου να είναι καμπυλωτό με δεξιά κλίση, ενώ το πίσω μέρος να είναι καμπυλωτό με αριστερή κλίση.

Αποδείξεις

Οι αποδείξεις των παραπάνω συμπερασμάτων, όπως αναφέραμε και παραπάνω μπορεί να ζητηθούν στο ανώτερο επίπεδο διαπραγμάτευσης, εφόσον το γνωστικό επίπεδο των μαθητών το επιτρέπει και θα συνδυάζει την εποπτεία με τη μαθηματική αυστηρότητα και φορμαλισμό. Οι μαθητές πρέπει να καταλάβουν ότι τα αποτελέσματα που προέκυψαν με την παρατήρηση, τον πειραματισμό και την εποπτεία δεν αποτελούν στέρεα μαθηματική γνώση χωρίς την πιστοποίηση της απόδειξης. Αυτό τουλάχιστον υπαγορεύει η έγκυρη μαθηματική πρακτική, η οποία έχει ιστορία και παράδοση 2500 χρόνων. Οι αποδείξεις θα γίνουν με αναφορά σε ένα απλό σχήμα, όπως αυτό της εικόνας 6, το οποίο οι μαθητές θα σχεδιάσουν στο τετράδιο τους.

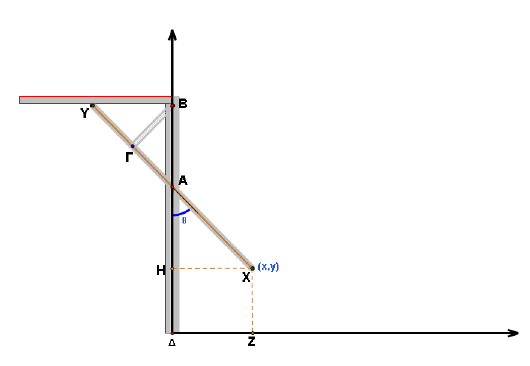
εικόνα 6

1. Επειδή το σημείο Γ απέχει πάντα σταθερή απόσταση ΓΒ=0,5m από το σταθερό σημείο Β, θα διαγράφει περιφέρεια κύκλου με κέντρο Β και ακτίνα ρ=0,5m.
2. Αφού ΒΓ=ΥΓ=ΓΑ=0,5m, το τρίγωνο ΥΒΑ είναι πάντα ορθογώνιο στο Β. Επομένως, το Β θα βρίσκεται πάντα σε μια ημιευθεία ΥΒ κάθετη στη ΒΔ στο σημείο Β.
3. Τοποθετούμε το γεωμετρικό μοντέλο κατάλληλα σε ένα ορθογώνιο σύστημα συντεταγμένων με το σημείο Δ να συμπίπτει με την αρχή των αξόνων και το ΔΒ πάνω στον άξονα y΄y, όπως στην εικόνα 6. Έστω (χ, ψ) οι συντεταγμένες του σημείου Χ και θ η γωνία που σχημα τίζει η πόρτα ΧΥ με την κατακόρυφη δοκό ΒΔ. Όταν κλείσει η πόρτα ΧΥ θα καλύψει εντελώς το ευθύγραμμο τμήμα ΒΔ. Συνεπώς ΒΔ=ΧΥ=2m. Επειδή ΑΥ=1m, θα είναι ΑΧ=ΧΥ-ΑΥ=1m. Άρα θα ισχύει πάντα ότι το Α είναι το μέσο της ΧΥ. Από τα όμοια τρίγωνα ΥΒΑ και ΑΗΧ, το Α θα είναι το μέσο του ΒΗ.. Άρα . Επομένως οι συντεταγμένες του Χ θα είναι χ=ημθ και y=2(1-συνθ). Από τις σχέσεις αυτές προκύπτει ότι και αντικαθιστώντας τα συνθ και ημθ στη βασική τριγωνομετρική ταυτότητα θα έχουμε (1). Η (1) παριστάνει την εξίσωση μιας έλλειψης με κέντρο το σημείο Β(0,2) και εστίες Ε΄(0,2-) και Ε(0,2) πάνω στον άξονα y΄y.
4. Εάν υποθέσουμε ότι το ύψος του κατακόρυφου μπροστινού τμήματος του αυτοκινήτου είναι α > 0, η θέση με την ελάχιστη απόσταση θα είναι εκείνη κατά την οποία το Ζ θα συναντά την έλλειψη. Τότε στη θέση αυτή το σημείο Ζ θα έχει συντεταγμένες έστω (d, α) και αφού βρίσκεται πάνω στην έλλειψη οι συντεταγμένες θα επαληθεύουν την (1). Άρα  και (2). Στην περίπτωσή μας, όπου α= 0,58m, θα έχουμε ότι d=0,7m.

Συμπέρασμα

Οι κατάλληλα επιλεγμένες προβληματικές καταστάσεις που έχουν κάποιο νόημα για τους μαθητές μπορούν να λειτουργήσουν ως εφαλτήριο για την ενεργοποίηση τους και τη δημιουργική ενασχόλησή με το μαθηματικό γίγνεσθαι. Στην παραπάνω δραστηριότητα περιγράψαμε ένα πραγματικό πρόβλημα και αναλύσαμε τη διαδικασία προσέγγισής του σε περιβάλλον δυναμικής γεωμετρίας. Η επιλογή αυτή έδωσε τη δυνατότητα στους μαθητές να πειραματιστούν, να εξερευνήσουν, να διατυπώσουν υποθέσεις, να ελέγξουν εικασίες και να αποδείξουν συμπεράσματα, ενέργειες που συνιστούν την πεμπτουσία της μαθηματικής δημιουργίας (Stanley, 1998).

Tα εκπαιδευτικά λογισμικά προσφέρουν κατάλληλα περιβάλλοντα για τη διερεύνηση προβλημάτων, λειτουργώντας ως εργαλείο στη διάθεση του μαθητή όσο και του δασκάλου. Ο πρώτος χρειάζεται την κατάλληλη δόση τ βοήθειας και υποστήριξης, προκειμένου να «πάρει μπρος» και να αυτενεργήσει, χωρίς να κινδυνεύει από πνευματική ασφυξία κάτω από την πλήρη κηδεμονία και επιτήρηση του δασκάλου. Ο δεύτερος πρέπει να είναι σε θέση να ενεργοποιεί τους μαθητές, σχεδιάζοντας γόνιμα περιβάλλοντα μάθησης και αξιοποιώντας όσο το δυνατόν καλύτερα τις δυνατότητες που προσφέρουν τα σύγχρονα τεχνολογικά εργαλεία.

ΑΝΑΦΟΡΕΣ

• Hirschhorn, D. & Thompson, D. (1996): “Technology and Reasoning in Algebra and Geometry” The mathematics Teacher 89(2), 138-142.
• Kanold, T. (1990): “Effective Mathematics Teaching: One Perspective” in Teaching and Learning Mathematics in 1990s, edited by T. Cooney & C. Hirsch, 76-82. Reston. Va.: NCTM.
• National Council of Teachers of Mathematics (1991): Professional Standards for Teaching Mathematics. Reston. Va.: The Council.
• Oldknow, A. & Taylor, R. : Teaching Mathematics using ICT, 2nd Edition, Continuum, N.York
• Stanley, I. (1998): “Proof in Modern Geometry” The mathematics Teacher 91(8), 718-721.
• Αρβανίτης, Τ. & Τουμάσης Μπ (2003): Διδασκαλία Μαθηματικών με Χρήση Η/Υ, Εκδόσεις Σαββάλας, Αθήνα.

ABSTRACT

A primary goal for teaching and learning mathematics is the development of mathematical power of all students. To accomplish this goal, teachers must select interesting and intellectually mathematical tasks, promote the investigation of mathematical ideas and use technology to pursue these investigations. In this paper we present a problem situation, which is analyzed into a dynamic geometry environment and offers students a rich experience of “what mathematics is, and what it means to know and do mathematics”.