
ΤΟ ΓΕΩΜΕΤΡΙΚΟ ΠΡΟΒΛΗΜΑ: ΚΙΝΗΤΡΑ ΓΙΑ ΑΠΟΔΕΙΞΗ ΣΕ ΕΝΑ ΔΥΝΑΜΙΚΟ ΓΕΩΜΕΤΡΙΚΟ ΠΕΡΙΒΑΛΛΟΝ.
Νόρμαν 33, 262 23, Πάτρα
Τηλ: 2610-455003
Περίληψη
Η αυξανόμενη χρήση των υπολογιστών, τόσο στα μαθηματικά όσο και στη μαθηματική εκπαίδευση, έχει επηρεάσει σημαντικά τη διδασκαλία της γεωμετρίας. Η ανάπτυξη του δυναμικού γεωμετρικού λογισμικού τα τελευταία χρόνια, εκτός του ότι αναζωπύρωσε το ενδιαφέρον για κάποια βασική έρευνα στη γεωμετρία, έχει αναζωογονήσει τη διδασκαλία της γεωμετρίας σε πολλές χώρες. Η χρήση, βέβαια, της δυναμικής γεωμετρίας έχει προκαλέσει επίσης, μια ριζική αλλαγή στη διδασκαλία της απόδειξης. Σ’ αυτήν την εργασία θεωρούμε κάποιες διαφορετικές λειτουργίες της απόδειξης στα μαθηματικά και συζητάμε το σχεδιασμό γεωμετρικών δραστηριοτήτων, οι οποίες θα μπορούσαν να προκαλέσουν το ενδιαφέρον για απόδειξη.
Η αυξανόμενη χρήση των υπολογιστών στα μαθηματικά αυτά καθ’ αυτά, όσο και στη μαθηματική εκπαίδευση με τη δημιουργία κατάλληλου λογισμικού, έχει επηρεάσει την τελευταία δεκαετία σημαντικά τη διδασκαλία των μαθηματικών και ιδιαίτερα της σχολικής γεωμετρίας. Δεν θα ήταν υπερβολή να ισχυριστούμε ότι το δυναμικό γεωμετρικό λογισμικό που έχει αναπτυχθεί πρόσφατα, αποτελεί την πιο σημαντική εξέλιξη στη γεωμετρία από την εποχή του Ευκλείδη.. Εκτός του ότι αναζωπύρωσε το ενδιαφέρον για κάποια βασική έρευνα στη στοιχειώδη Ευκλείδεια γεωμετρία, έχει επίσης αναζωογονήσει τη διδασκαλία της γεωμετρίας σε πολλές χώρες, όπου η Ευκλείδεια γεωμετρία βρισκόταν σε κίνδυνο να ριχτεί στο χρονοντούλαπο της ιστορίας (Davis, 1995. Oldknow, 1995).
Στο παρελθόν, οι περισσότεροι δάσκαλοι απέφευγαν την εμπειρική εξερεύνηση των γεωμετρικών συσχετίσεων επειδή οι κατασκευές με το μολύβι στο χαρτί, όσο και οι μετρήσεις με τα γεωμετρικά όργανα και τη χρήση άλλων μέσων, όπως, για παράδειγμα, διαφανούς χαρτιού, ήταν κουραστικές, χρονοβόρες και δεν παρείχαν μεγάλη ακρίβεια. Ένα άλλο πρόβλημα ήταν ότι τα σχήματα που κατασκευάζονταν με αυτό τον τρόπο ήταν στατικά και έπρεπε, προκειμένου να πειραματιστεί κανείς, είτε να ξανακατασκευάσει το σχήμα, είτε να φανταστεί νοερά πώς θα μπορούσε να αλλάξει μορφή όταν κάποια στοιχεία άλλαζαν θέση.
Όλα αυτά βεβαίως ανήκουν στο παρελθόν από τότε που δημιουργήθηκαν τα δυναμικά γεωμετρικά λογισμικά πακέτα. Δύο από τα πιο διαδεδομένα αυτά πακέτα είναι το Cabri-Geometry (Γαλλικό) και το Geometer’s Sketchpad (Αμερικάνικο). Αυτά τα λογισμικά σχεδιάστηκαν με την προοπτική να προσφέρουν ένα περιβάλλον μικρόκοσμου για την εξερεύνηση της στοιχειώδους επιπεδομετρίας. Τα γεωμετρικά σχήματα είναι δυνατόν να κατασκευαστούν με τη βοήθεια μενού τα οποία χρησιμοποιούν γλώσσα οικεία στο χρήστη από το περιβάλλον του «χαρτιού-και-μολυβιού». Μόλις κατασκευαστούν τα σχήματα αυτά είναι δυνατό να τροποποιηθούν και να αλλάξουν, «σύροντας» με το ποντίκι τα βασικά τους στοιχεία κατ’ ευθείαν από την οθόνη και μετακινώντας τα, ενώ διατηρούνται οι βασικές γεωμετρικές τους ιδιότητες.
Κατ’ αυτόν τον τρόπο κάποιος, για παράδειγμα, μπορεί να αλλάζει συνέχεια ένα τρίγωνο και ταυτόχρονα να παρατηρεί ότι τα ύψη του διέρχονται πάντα από το ίδιο σημείο. Το λογισμικό, επομένως, επιτρέπει σε κάποιον να εκτελεί εύκολα πειράματα, μεταβάλλοντας το σχήμα και να ελέγχει ποιες γεωμετρικές ιδιότητες παραμένουν αμετάβλητες (Τουμάσης & Αρβανίτης, 2003).
Ίσως, το πιο σπουδαίο, από παιδαγωγικής απόψεως, πλεονέκτημα του δυναμικού λογισμικού είναι οι δυνατότητές του να ενθαρρύνει τον πειραματισμό και την ερευνητική προσέγγιση στη μελέτη της γεωμετρίας. Σε μια τέτοιου τύπου προσέγγιση, οι μαθητές εξοικειώνονται νωρίς στην τέχνη της μαθηματικής δημιουργίας και ανακάλυψης, αφού προσφέρονται άφθονες ευκαιρίες για εξερεύνηση, διατύπωση εικασιών, ανασκευής και επαναδιατύπωσης αυτών και τελικού ελέγχου με την κατασκευή αποδείξεων (Τουμάσης 1999).
Στο σημείο αυτό βεβαίως, προκειμένου να μη δημιουργηθεί κάποια παρανόηση, θεωρούμε σημαντικό να τονίσουμε ότι τα μέχρι σήμερα υπάρχοντα λογισμικά, με όλα τα προαναφερθέντα παιδαγωγικά πλεονεκτήματα, δεν είναι σε θέση να αντικαταστήσουν τις αναλυτικές αποδείξεις, μολονότι οι υπηρεσίες που μπορούν να προσφέρουν στην κατασκευή μιας απόδειξης είναι σημαντικές (Bruchkheimer & Arcavi, 2001. Scher, 1999).
Ο ρόλος της απόδειξης σ’ ένα δυναμικό γεωμετρικό περιβάλλον.
Βεβαίως, όπως είναι φυσικό, η εμφάνιση του δυναμικού γεωμετρικού λογισμικού έχει δημιουργήσει τις προϋποθέσεις για μια ριζική αλλαγή στη διδασκαλία της απόδειξης.
Είναι γνωστό ότι η απόδειξη θεωρείται κεντρική για την επιστήμη των μαθηματικών και έχει καθοριστική σημασία για τη μαθηματική δραστηριότητα (Davis & Hersh, 1981). Η καλλιέργεια της έννοιας της απόδειξης, συνιστά επίσης ένα βασικό σκοπό της διδασκαλίας των μαθηματικών στη Δ/θμια εκπαίδευση, κυρίως στις ανώτερες τάξεις (Hirst, 1974. Quadling,1979).
Είναι γνωστό, επίσης, από σχετικές έρευνες, ότι στη συντριπτική πλειοψηφία τους οι μαθητές συναντούν μεγάλα προβλήματα στην κατανόηση της αποδεικτικής διαδικασίας και δεν είναι σε θέση να κατασκευάσουν ακόμα και απλές αποδείξεις γεωμετρικών προτάσεων (Fischbein, 1982. Senk, 1985).
O Schoenfeld (1989), αναφέρει, για παράδειγμα, ότι ακόμη κι όταν οι μαθητές αναπαράγουν μια τυπικά διδαγμένη ευκλείδεια απόδειξη, ένα σημαντικός αριθμός αυτών προτείνει μια λύση στο αντίστοιχο γεωμετρικό πρόβλημα κατασκευής, η οποία παραβιάζει ανοιχτά τα αποτελέσματα που οι ίδιοι έχουν ήδη αποδείξει.
Η τυπική παραδοσιακή προσέγγιση στη διδασκαλία της γεωμετρικής απόδειξης βασιζόταν στην προσπάθεια δημιουργίας αμφιβολιών στο μυαλό των μαθητών γύρω από την αξιοπιστία των εμπειρικών τους παρατηρήσεων, η οποία στη συνέχεια θα δημιουργούσε την ανάγκη και θα προσέφερε το κίνητρο για επιβεβαίωση μέσω μιας παραγωγικής απόδειξης.
Η κύρια, επομένως, λειτουργία της απόδειξης είναι παραδοσιακά αυτή της διαβεβαίωσης-επιβεβαίωσης ότι η ορθότητα μιας γεωμετρικής πρότασης είναι αληθής πέραν κάθε αμφιβολίας. Ο βασικός ρόλος της απόδειξης είναι να προσφέρει την τελική ετικέτα της αποδοχής και να αποτελέσει το εχέγγυο της αλήθειας μιας πρότασης (De Villiers, 1998).
Στο περιβάλλον όμως του δυναμικού γεωμετρικού λογισμικού, οι στρατηγικές αυτές που βασίζονται στη δημιουργία αμφιβολιών προκειμένου να προκληθεί η ανάγκη για μια απόδειξη, δεν φαίνεται να έχουν επιτυχία και αποτελεσματικότητα, αφού οι γεωμετρικές εικασίες έχουν ελεγχθεί εξαντλητικά, μέσω της δυνατότητας για απεριόριστες αλλαγές του γεωμετρικού σχήματος, που το δυναμικό λογισμικό προσφέρει. Είναι πολύ απλό. Όταν οι μαθητές είναι σε θέση να παράγουν αναρίθμητους σχηματισμούς γρήγορα και εύκολα, μέσα από τους οποίους αποκαλύπτονται οι γεωμετρικές ιδιότητες, τότε δεν τους δημιουργείται η ανάγκη για παραπέρα επιβεβαίωση. Έχουν πειστεί ήδη για την αλήθεια μιας πρότασης ή για την ορθότητα ενός ισχυρισμού.
Επομένως, εάν περιοριστούμε στην παραδοσιακή αντίληψη για τον επιβεβαιωτικό – διαπιστωτικό ρόλο της απόδειξης, μοιραία οδηγούμαστε στο συμπέρασμα ότι στα πλαίσια ενός δυναμικού γεωμετρικού περιβάλλοντος η αξία της απόδειξης μειώνεται, μέχρι το σημείο να θεωρηθεί μη αναγκαία, προς όφελος μιας εντελώς εμπειρικής – πειραματικής προσέγγισης για την εξασφάλιση της αλήθειας μιας γεωμετρικής πρότασης. Διαφαίνεται έτσι ο κίνδυνος να καταλήξει κανείς στο συμπέρασμα ότι στα πλαίσια ενός υπολογιστικού περιβάλλοντος εξερεύνησης της μαθηματικής γνώσης, είναι δυνατόν να ελεγχθεί ένας μεγάλος αριθμός περιπτώσεων, ο οποίος λόγω της συνεχούς κίνησης μπορεί να θεωρηθεί άπειρος, έτσι ώστε η αλήθεια να εδραιωθεί πάνω στις παρατηρήσεις που προκύπτουν από άπειρες περιπτώσεις, οι οποίες εξερευνούνται ταχέως με τη βοήθεια ενός computer.
H άποψη αυτή αντανακλά την τάση που παρατηρείται σήμερα μεταξύ κάποιων επαγγελματιών μαθηματικών και μαθηματικών παιδαγωγών, να παρερμηνεύουν την αυξανόμενη χρήση της υπολογιστικής τεχνολογίας στη μαθηματική επιστήμη και να στηρίζουν, έτσι, την πεποίθησή τους ότι μελλοντικά η απόδειξη θα πάψει να συνιστά την κεντρική πλευρά της μαθηματικής θεωρίας και πρακτικής (Τουμάσης, 2000).
Παρ’ όλα αυτά η συντριπτική πλειοψηφία των μαθηματικών αλλά και των δασκάλων που διδάσκουν μαθηματικά θα συμφωνούσε, ασφαλώς, στο ότι οι μαθητές είναι αναγκαίο να συνειδητοποιήσουν ότι η εξερεύνηση και ο πειραματισμός, όσο πολύτιμες διαδικασίες κι αν συνιστούν για το σχηματισμό και τον έλεγχο των εικασιών και υποθέσεων, σε καμιά περίπτωση δεν συνιστούν απόδειξη, ούτε και είναι σε θέση να την αντικαταστήσουν. Θα συμφωνούσαν επίσης, στο ότι η μεγάλη πρόκληση συνίσταται στο να καταφέρουν να παρακινήσουν τους μαθητές να διαμορφώσουν μια απόδειξη ή τουλάχιστον να προσπαθήσουν να παρακολουθήσουν τα βήματα μιας απόδειξης που παρουσιάζεται από το δάσκαλο.
Ακόμη και το πιο ισχυρό δυναμικό λογισμικό δεν είναι σε θέση να προσφέρει το βαθμό της βεβαιότητας που προσφέρει μια αναλυτική απόδειξη. Ακόμη πιο σημαντικό όμως για την εκπαιδευτική διαδικασία μάθησης των μαθηματικών είναι να επιτευχθεί πραγματική κατανόηση μιας έννοιας ή ενός αποτελέσματος. Η πραγματική κατανόηση όμως απαιτεί να «δουν» οι μαθητές και να συνειδητοποιήσουν γιατί ισχύει ένα συμπέρασμα και ακόμη παραπέρα γιατί πρέπει να ισχύει πάντοτε. Ποιοι είναι αυτοί οι λόγοι ή ποιες είναι οι μαθηματικές ιδέες, οι οποίες συνέβαλαν στο να συμβεί κάποιο μαθηματικό γεγονός.
Αν και οι μαθητές σ’ ένα δυναμικό γεωμετρικό περιβάλλον αισθάνονται σίγουροι για την αλήθεια κάποιας εικασίας, ο δάσκαλος έχει καθήκον να τους κεντρίσει παραπέρα την περιέργειά τους, ζητώντας τους να διερευνήσουν για πιο λόγο πιστεύουν ότι το συγκεκριμένο αποτέλεσμα είναι αληθές. Να τους προκαλέσει να προσπαθήσουν να δώσουν μια εξήγηση, η οποία θα ρίχνει φως στον τρόπο με τον οποίο συντίθεται το παζλ και θα κατορθώνει να παρουσιάσει το αποτέλεσμα ως λογική συνέπεια άλλων γνωστών αποτελεσμάτων.
Επομένως, η εμφάνιση της τεχνολογίας, τόσο στα μαθηματικά αυτά καθ’ αυτά όσο και στη μαθηματική εκπαίδευση, μας αναγκάζει να τονίσουμε κάποιες άλλες λειτουργίες της απόδειξης, οι οποίες είχαν επισκιαστεί από την παραδοσιακά κυρίαρχη λειτουργίας της διαβεβαίωσης και επιβεβαίωσης της αλήθειες. Αυτές οι λειτουργίες σύμφωνα με τον De Villiers (1998) συνίστανται:
Στην επεξήγηση (εξηγούν γιατί μια πρόταση είναι σωστή).
Στην ανακάλυψη (ανακάλυψη ή επινόηση των νέων αποτελεσμάτων).
Στη συστηματοποίηση (οργάνωση των αποτελεσμάτων σ’ ένα παραγωγικό σύστημα με αξιωματική θεμελίωση).
Στη διανοητική πρόκληση (η αυτοεπιβεβαίωση – εκπλήρωση που γεννιέται από την κατανόηση μιας από9δειξης).
Στην επικοινωνία (η μεταφορά και η διάδοση της μαθηματικής γνώσης).
Η μεγάλη πρόκληση λοιπόν για το δάσκαλο των μαθηματικών σ’ ένα δυναμικό περιβάλλον διδασκαλίας και μάθησης της γεωμετρίας, συνίσταται στο να βρει τρόπους να προβάλει και τις εξερευνητικές, επεξηγηματικές, οργανωτικές και επικοινωνιακές λειτουργίες της απόδειξης, παράλληλα με την επιβεβαιωτική και διαπιστωτική λειτουργία (Ηoyles and Jones, 1998, p.122). Προς αυτή την κατεύθυνση σημαντικό είναι να εξευρεθούν κατάλληλα προβλήματα ή δραστηριότητες, τα οποία θα βοηθούν το έργο της ανάδειξης των παραπάνω λειτουργιών της απόδειξης και θα παρακινούν ταυτόχρονα τους μαθητές να πειραματιστούν, να εξερευνήσουν, να ανακαλύψουν και να εξηγήσουν γιατί ένα αποτέλεσμα, το οποίο παρατηρούν στην οθόνη του υπολογιστή, πρέπει να είναι αληθές.
Αναζήτηση κατάλληλων γεωμετρικών προβλημάτων.
Τα μαθηματικά προβλήματα ή ασκήσεις, που περιλαμβάνονται παραδοσιακά στα σχολικά βιβλία γεωμετρίας, είναι κλειστού τύπου. Το βασικό τους χαρακτηριστικό συνίσταται στο ότι είναι τόσο καλά διατυπωμένα ώστε επιδέχονται μία μόνο σωστή απάντηση. Τα προβλήματα αυτά ξεκινούν περιγράφοντας μια κατάσταση, η οποία οδηγεί στο σχηματισμό ενός γεωμετρικού σχήματος και ζητείται από τους μαθητές να αποδείξουν κάποιες ιδιότητες αυτού του συγκεκριμένου σχηματισμού. Αναφέρουμε, για παράδειγμα, ένα τέτοιο αντιπροσωπευτικό πρόβλημα, το οποίο περιλαμβάνεται στο σχολικό βιβλίο γεωμετρίας για το Λύκειο (Αργυρόπουλος κ.α., 2001, σελ.100).
Δίνεται τρίγωνο ΑΒΓ. Στις προεκτάσεις των διαμέσων ΒΔ και ΓΕ παίρνουμε τα σημεία Η και Ζ αντίστοιχα, τέτοια ώστε ΔΗ = ΒΔ και και ΖΕ = ΓΕ. Να αποδείξετε ότι i) AH = AZ και ii) tτα σημεία Ζ, Α και Η είναι συνευθειακά.

Η διατύπωση του παραπάνω προβλήματος δεν αφήνει περιθώρια στους μαθητές για πειραματισμό, εξερεύνηση, ανακάλυψη, διατύπωση και έλεγχο εικασιών και γενικά για δημιουργική εργασία η οποία θα καταλήγει φυσιολογικά στην απόδειξη μιας πρότασης. Το αποτέλεσμα είναι προκαθορισμένο, είναι σίγουρο δηλαδή, ότι είναι αληθές και απλώς οι μαθητές διατάσσονται να το αποδείξουν, χωρίς να προσφέρεται κανένα κίνητρο γι’ αυτό.
Έρευνες στη διδακτική των μαθηματικών αποκαλύπτουν ότι προβλήματα διατυπωμένα με τον παραπάνω τρόπο, δηλαδή, «Να αποδείξετε ότι….», σε ορισμένες περιπτώσεις φρενάρουν την ικανότητα των μαθητών για απόδειξη (Boero et al, 1996). Άλλες έρευνες, επίσης, αναδεικνύουν τη σημασία που έχει η επιλογή του πλαισίου ή της διατύπωσης μιας δραστηριότητας μέσα στην τάξη για την ενεργοποίηση της διανοητικής διαδικασίας, η οποία θα θέσει σε λειτουργία τη δυναμική εξερεύνηση μιας προβληματικής κατάστασης με τη δημιουργία υποθέσεων και εικασιών (Αrzarello et al, 1998).
Είναι προφανές ότι η ίδια η διατύπωση του παραπάνω προβλήματος προοιωνίζει από μόνη της δυσκολίες στη μαθησιακή διαδικασία, αφού δεν είναι σε θέση να παρακινήσει ουσιώδεις διανοητικές λειτουργίες στα πλαίσια μιας ανακαλυπτικής προσέγγισης. Εξάλλου, έρευνες στη διδακτική των μαθηματικών αποδεικνύουν ότι τα προβλήματα κλειστού τύπου, όπως το παραπάνω, εγκλωβίζουν τους μαθητές στη θεωρητική φορμαλιστική πλευρά της γεωμετρίας, εμποδίζουν την απελευθέρωση των δημιουργικών τους ικανοτήτων και τελικά υπονομεύουν τη δυνατότητα για απόδειξη (Shimada, 1997).
Απεναντίας, μια ανοιχτή προβληματική κατάσταση θα μπορούσε να προσφέρει περισσότερες ευκαιρίες στους μαθητές για ενεργητική συμμετοχή στη διαδικασία μάθησης και να τους παρακινήσει να εμπλακούν σε δραστηριότητες, οι οποίες θα καλύπτουν όλο το φάσμα της μαθηματικής δημιουργίας και ανακάλυψης (Simon, 1998). Η ιδέα αυτή βασίζεται στην υπόθεση ότι η απόδειξη ενός αποτελέσματος, το οποίο έχει ανακαλυφθεί και διαπιστωθεί από τους ίδιους τους μαθητές ως το προϊόν εμπειρικών παρατηρήσεων και πειραματισμών, τους προξενεί μεγαλύτερη αίσθηση παρά η απόδειξη μιας πρότασης, η οποία τους δίνεται έτοιμη και την οποία τις περισσότερες φορές δεν την καταλαβαίνουν. Επιπροσθέτως, τα ανοιχτά προβλήματα, τα οποία ευνοούν τη δυναμική διερεύνηση μιας κατάστασης, προσφέρουν στους μαθητές τη δυνατότητα να ανακατασκευάσουν μέσα από τις ιδιότητες και συσχετίσεις, όλα τα στοιχεία που είναι απαραίτητα για την απόδειξη.
Η κατασκευή ανοιχτών προβλημάτων, που
θα εξυπηρετούν κάθε φορά συγκεκριμένους διδακτικούς στόχους, δεν είναι μια εύκολη υπόθεση. Απαιτεί επινοητικότητα και φαντασία, καθώς επίσης και άριστη γνώση των συνθηκών διδασκαλίας και μάθησης. Ένας εύκολος τρόπος δημιουργίας μιας δεξαμενής ανοιχτών προβλημάτων είναι η κατάλληλη μετατροπή του κλειστού τύπου προβλημάτων, που αφθονούν στα σχολικά βιβλία, σε ανοικτού τύπου.
Ένα ανοιχτό γεωμετρικό πρόβλημα είναι συνήθως της μορφής :
« Εάν ισχύουν οι προτάσεις P1, P2, …, Pκ, τότε ποιες συσχετίσεις μεταξύ των στοιχείων του σχήματος μπορείς να διακρίνεις; Ποιες ιδιαιτερότητες του σχήματος μπορείς να ανακαλύψεις; Ποιες υποθέσεις μπορείς να κάνεις σχετικά με τις ιδιότητες των στοιχείων που απαρτίζουν το σχήμα;».
Ακολουθώντας, για παράδειγμα, την τεχνική αυτή, το πρόβλημα κλειστού τύπου που παρουσιάσαμε παραπάνω μπορεί να μετασχηματιστεί στο εξής πρόβλημα ανοικτού τύπου, κατάλληλο για επεξεργασία σ’ ένα δυναμικό γεωμετρικό περιβάλλον :
Δίνεται τρίγωνο ΑΒΓ. Στις προεκτάσεις των διαμέσων ΒΔ και ΓΕ παίρνουμε σημεία Η και Ζ αντίστοιχα, τέτοια ώστε ΔΗ = ΒΔ και ΖΕ = ΓΕ. Ποιες συσχετίσεις μπορείτε να βρείτε μεταξύ των σημείων, τμημάτων και γωνιών που απαρτίζουν το σχήμα;
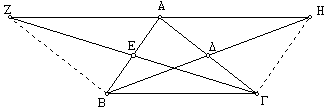
Οι μαθητές αφού ενώσουν κάποια σημεία, μπορούν να αξιοποιήσουν τα μενού των γεωμετρικών λογισμικών (Cabri ή Sketchpad) και να ανακαλύψουν, για παράδειγμα, ότι:
ΒΖ
= ΑΓ, ΓΗ = ΑΒ,
ΖΑ = ΒΓ, ΑΗ
= ΒΓ, ![]()
και ότι Ζ, Α, Η συνευθειακά.
Προκειμένου να λύσουν το παραπάνω πρόβλημα, οι μαθητές πρέπει να πάρουν αποφάσεις για την επιλογή μιας στρατηγικής, αφού πρώτα ανακαλύψουν κάποιο αποτέλεσμα, το οποίο μπορεί να μην είναι το μοναδικό. Είναι ελεύθεροι να θέσουν ερωτήματα αντί να απαντήσουν μόνο σε προκαθορισμένα, να διατυπώσουν εικασίες, να τις αξιολογήσουν και εν τέλει να τις αποδείξουν. Η διαδικασία της λύσης αποκτά έτσι ισοδύναμη αξία με τη λύση αυτή καθ’ αυτή, ενώ ο στόχος δεν είναι μόνο στο να παραχθεί το σωστό αποτέλεσμα, αλλά πώς να παραχθεί ένα οποιοδήποτε αποτέλεσμα. Το κίνητρο για απόδειξη, η οποία θα εξηγεί για ποιο λόγο συνέβη το ένα ή το άλλο γεγονός ή αποτέλεσμα, καθίσταται έτσι ισχυρό.
Αργυρόπουλος, Η. κ.α. (2001): Ευκλείδεια Γεωμετρία Α΄ και Β΄ Ενιαίου Λυκείου. Αθήνα, Ο.Ε.Δ.Β.
Arzarello, F., Micheletti, C., Olivera, F., Robutti, O. and Paola, D. (1998):
“A model for analyzing the transition to formal proofs in Geometry”. Proceedings of the 22nd Conference of the International Group for the Psychology of Mathematical Education. Stellenbosch, South Africa, Vol. 2, 24-31.
Boero, P., Garuti, R. and Marriotti, M.(1996): “ Some dynamical mental processes underlying processing and proving conjectures”. Proceedings of the 20th Conference of the International Group for the Psychology of Mathematical Education. Valencia, Spain, vol.2, 121-128.
Bruckheimer, M. and Arcavi, A. (2001): “A Herrick among mathematicians or dynamic geometry as an aid to proof ”. International Journal of Computers for Mathematical Learning, 6, 113-126.
Davis, P. & Hersh, B. (1981): The mathematical Experience. Boston, MA, Birkhauser.
Davis, P. (1995): “The rise, fall, and possible transfiguration of triangle Geometry”. American Mathematical Monthly, 102(3), 204 – 214.
De Villiers, M. (1998) : “An alternative Approach to Proof in Dynamic Geometry”, In R. Lehrer and D. Chazan (Eds): Designing Learning Enviroments for developing Understanding of Geometry and Space Hillsdale, NJ, Lawrence Erlbaum Associates.
De Villiers, M. (1999) : Rethinking Proof with the Geometer’s Sketchpad. Key curriculum Press.
Hirst, P. H. (1974). Knowledge and the Curriculum. London, Rutledge & Kegan Paul.
Hoyles, C. and Jones, K. (1998): “Proof in Dynamic Geometry Contexts”. In C. Mammana and V. Vilani (Eds), Perspectives on the Teaching of Geometry for the 21st Century. Dordrecht: Kluwer.
Oldknow A. (1995): “Computer aided research into triangle geometry”. The mathematical Gazette, 79(485), 263-274.
Quadling, D. (1979): “Mathematical Education at upper secondary school, college and university transition”, In ICMI, New Trends in Mathematics Teaching, Paris, UNESCO.
Scher, D. (1999): “ Problem solving proof in the age of dynamic geometry”. Micromath, 15(1), 24-30.
Schoenfeld, A. (1989): “Explorations of students’ mathematical beliefs and behavior”. Journal for Research in Mathematics Education, 20(4), 338-355.
Shimada, S. (1997): “The significance of an open-ended approach, In J. Becker and S. Shimada (Eds): The Open-Ended Approach: a new proposal for teaching mathematics, NCTM, Reston, VA.
Simon, M. (1996): “Beyond Inductive and Deductive Reasoning: the search for a sense of Knowing”. Educational studies in mathematics, 30, 197- 210
Τουμάσης Μπ. (1999): Σύγχρονη Διδακτική των Μαθηματικών. Εκδ. Gutenberg.
Τουμάσης Μπ. (2000): «Αλλάζει η φύση της μαθηματικής απόδειξης; παιδαγωγικές συνέπειες». Ευκλείδης Γ΄ , 16(52), 5-25.
Τουμάσης Μπ., Αρβανίτης Τ. (2003): Διδασκαλία μαθηματικών με χρήση Η/Υ. Εκδ. Σαββάλας
ABSTRACT
The increasing use of computers in mathematics education is strongly reflected in the teaching of geometry. The development of dynamic geometry software in recent years besides rekindling interest in some basic research in geometry, it has revitalized the teaching of geometry in many countries. However, the use of dynamic geometry has also necessitated a radical change to the teaching of proof. In this paper we consider some different functions of proof into mathematics and discuss the design of geometrical tasks that could provide the motivation to prove.