Η παρακάτω εργασία παρουσιάστηκε στο 19ο πανελλήνιο συνέδριο Μαθηματικής παιδείας που έγινε στην Κομοτηνή το φθινόπωρο του 2002
Μαθηματικά και τέχνη: Διακοσμητικά σχήματα με χρήση γεωμετρικού λογισμικού
Μπάμπης Τουμάσης Τάσος Αρβανίτης
Στην εργασία αυτή συζητάμε πρώτα ορισμένες πλευρές της μαθηματικής τέχνης. Μολονότι τα μαθηματικά και η τέχνη είναι δυο διακριτά πεδία, σύμφωνα με τις σύγχρονες αντιλήψεις, υπάρχει ένας αριθμός καλλιτεχνών οι οποίοι κάνουν τα μαθηματικά επίκεντρο της δουλειάς τους όπως υπάρχουν επίσης και πολλά θέματα τα οποία έχουν χρησιμοποιηθεί ευρέως από την μαθηματική τέχνη. Μεταξύ αυτών περιλαμβάνονται πολύεδρα ψηφιδωτά, ανέφικτα σχήματα, ταινίες Möbious, ασυνήθιστα προοπτικά συστήματα και fractals. Στη συνέχεια παρουσιάζουμε κάποιες ιδέες για την κατασκευή διαφόρων τύπων ψηφιδωτών αξιοποιώντας κάποιες εντολές του γεωμετρικού λογισμικού Geometer’s Sketchpad όπως μετατόπιση, περιστροφή, ανάκλαση καθώς επίσης και αρχεία εντολών. Όλες αυτές οι ιδέες και υποδείξεις μπορεί να χρησιμοποιηθούν προκειμένου να βοηθήσουν τους μαθητές να δημιουργήσουν δικά τους ψηφιδωτά με την βοήθεια του Geometer’s Sketchpad.
Μαθηματική τέχνη
Τα μαθηματικά και η τέχνη γενικότερα μολονότι, φαινομενικά τουλάχιστον, αποτελούν δυο ξεχωριστά – διακριτά πεδία της ανθρώπινης δραστηριότητας, εντούτοις είναι δυνατόν να συνδυαστούν και να δώσουν δημιουργίες οι οποίες αποτελούν αξιοθαύμαστο μείγμα εντυπωσιακής πολυπλοκότητας και εκπληκτικής ομορφιάς.
Ιστορικά, τα μαθηματικά, μολονότι θεωρούνται κυρίως λογική – αναλυτική επιστήμη, έχουν παίξει σημαντικό ρόλο στην εξέλιξη της τέχνης, η οποία απευθύνεται κυρίως στο συναίσθημα. Δυο αιώνες πριν οι αρχαίοι Έλληνες επεξεργαστούν τις αφηρημένες γεωμετρικές ιδέες, και θεμελιώσουν επιστημονικά τη γεωμετρία, οι Αιγύπτιοι, τους οποίους απασχολούσαν ελάχιστα τα θεωρητικά ζητήματα, χρησιμοποιούσαν τα εργαλεία τους προκειμένου να σχεδιάσουν και οικοδομήσουν τους έξοχους ναούς και τα εκπληκτικά μνημεία τους. Για τους Αιγυπτίους η γεωμετρία ήταν ένα σύνολο εμπειρικών γνώσεων κατάλληλων για τους εξερευνητές της γης, τους καλλιτέχνες, τους αρχιτέκτονες, τους μηχανικούς και τους γλύπτες. Αποτελούσε πρωτίστως ένα εργαλείο που τους προσέφερε την δυνατότητα να εκτελούν πρακτικές και καλλιτεχνικές εργασίες ([5], [10]).
Τα μαθηματικά από τότε μέχρι και σήμερα εξακολουθούν να παίζουν ένα σημαντικό ρόλο στην εξέλιξη των διαφόρων μορφών της τέχνης [12]. Σ’ όλες τις εποχές αναδείχθηκαν εξέχουσες μορφές της τέχνης, οι οποίες χρησιμοποίησαν τα μαθηματικά ως το βασικό συστατικό της τέχνης τους. Είναι προφανές ότι δεν είναι δυνατόν να υπάρξουν κανόνες ή όρια σχετικά με τα θέματα ή τις ιδέες της μαθηματικής τέχνης. Υπάρχουν όμως κάποια θέματα τα οποία έχουν χρησιμοποιηθεί περισσότερο και δείχνουν ότι έχουν κερδίσει την προτίμηση ορισμένων καλλιτεχνών. Μεταξύ αυτών είναι τα πολύεδρα, τα ψηφιδωτά, τα ανέφικτα σχήματα, οι ταινίες Möbious και τα fractals.
Ο Ευκλείδης (300 π.χ.) στο 13ο βιβλίο των «Στοιχείων» του απέδειξε ότι υπάρχουν ακριβώς πέντε τύποι κανονικών πολυέδρων: το τετράεδρο, το οκτάεδρο, ο κύβος, το δωδεκάεδρο και το εικοσάεδρο [2]. Ο Πλάτωνας (427-348 π.χ.) έτρεφε ένα τόσο μεγάλο θαυμασμό απέναντι σ’ αυτά τα σχήματα ώστε τα χρησιμοποίησε στο κοσμολογικό του σύστημα προκειμένου να απεικονίσει τα τέσσερα βασικά στοιχεία του σύμπαντος – τη γη, τον αέρα, τη φωτιά και το νερό. Τα «Πλατωνικά στερεά», όπως είναι γνωστά τα κανονικά αυτά πολύεδρα, έχουν χρησιμοποιηθεί κατά καιρούς σε πολλά και διάφορα έργα τέχνης ως διακοσμητικά στοιχεία.
Ο Leonardo da Vinci (1402-1519) είναι γνωστός για τα επιτεύγματά του τόσο στις επιστήμες όσο και στις καλές τέχνες. Στα έργα του χρησιμοποίησε παραστατική γεωμετρία προκειμένου να δημιουργήσει τα πρώτα παραμορφωμένα πλέγματα, τα οποία όταν ειδωθούν από κάποια συγκεκριμένη γωνία εμφανίζονται κανονικά. Ο Johanes kepler (1580-1630) επίσης πέρα από τη αστρονομία είχε μεγάλο ενδιαφέρον για τη δημιουργία γεωμετρικών ψηφιδωτών.
Όταν όμως αναφερόμαστε στον όρο «μαθηματική τέχνη» ο νους μας πηγαίνει κυρίως στον Ολλανδό καλλιτέχνη Maurits Escher (1898-1972), ο οποίος δικαίως θεωρείται ο πατέρας αυτού του είδους της τέχνης. Η εργασία του αποτελεί μια αστείρευτη πηγή έμπνευσης για πολλούς σύγχρονους σημαντικούς καλλιτέχνες. Οι λιθογραφίες, οι ξυλογλυφίες και οι χαλκογραφίες του βρίσκονται κρεμασμένες στα σπίτια μαθηματικών και επιστημόνων σ’ όλο τον κόσμο. Πολλά έργα του έχουν ως βάση κάποια μαθηματικά θέματα που έχουν κατά καιρούς αναλυθεί σε βιβλία ψυχαγωγικών μαθηματικών, όπως αυτά του Martin Gardner. Ο Escher είναι περισσότερο γνωστός στους κρυσταλλογράφους για την πετυχημένη ψηφιδωτή τεχνική με την οποία χωρίζει το επίπεδο. Χωρίζοντας το επίπεδο με κυματιστές σειρές πουλιών, ψαριών, ερπετών, θηλαστικών και ανθρώπων κατάφερε να δημιουργήσει μεγάλη ποικιλία καταπληκτικών όσο και απροσδόκητων εικόνων, οι οποίες βασίζονται σε νόμους της συμμετρίας, της θεωρίας συνόλων, της προοπτικής, της τοπολογίας και της κρυσταλλογραφίας ([1],[4]).
Ο Salvator Dali (1904-1989) ήταν ένας άλλος διάσημος Ισπανός σουρεαλιστής ζωγράφος ο οποίος χρησιμοποίησε στους πίνακές του σχέδια με έντονα γεωμετρικά-τοπολογικά στοιχεία. Ο Dali απεικόνισε σε πολλά έργα του τον τετραδιάστατο χώρο στο χώρο των δύο διαστάσεων. Για παράδειγμα, στο έργο «Σε αναζήτηση της τέταρτης διάστασης», υπάρχουν στοιχεία τοπολογίας και τετραδιάστατης γεωμετρίας, έτσι που ο πίνακας φαίνεται να κινείται γύρω από μια υπερσφαίρα.
Στα τέλη του 19ου αιώνα – αρχές του 20ου, μια ομάδα μαθηματικών με επικεφαλής τους Peano, Hilbert, Cesaro, Koch και Sierprinski, μεταξύ άλλων, διαμόρφωσαν μια νέα οικογένεια καμπύλων με αλλοπρόσαλλες μαθηματικές ιδιότητες, οι οποίες ξέφευγαν από κάθε άλλο προηγούμενο. Αντίθετα προς την παραδοσιακή γεωμετρία που βασιζόταν στα τρίγωνα, τα τετράγωνα, τους κύκλους, τις ελλείψεις κλπ, αυτή η νέα γεωμετρία περιγράφει περιστρεφόμενες καμπύλες, σπιράλ και ίνες οι οποίες περιτυλίσσονται μεταξύ τους έτσι ώστε να δίνουν περίπλοκα σχήματα, οι λεπτομέρειες των οποίων να χάνονται στο άπειρο.
Το 1977, με τη βοήθεια ενός Computer, ο Γάλλο-Πολωνικής καταγωγής επιστήμονας Benoit Mandelbrot, κατόρθωσε να πάρει την πρώτη εικόνα αυτής της νέας γεωμετρίας, η οποία στη συνέχεια ονομάστηκε Φράκταλ γεωμετρία. Το 1980, η δημοσίευση του βιβλίου του με τίτλο «Η φράκταλ γεωμετρία στη φύση», έκανε δημοφιλή τη γεωμετρία αυτή και είχε ως αποτέλεσμα τη δημιουργία ανάλογων εντυπωσιακών σχημάτων.
Την
τελευταία δεκαετία διαφαίνεται μια τάση
για παραπέρα ανάπτυξη των αποκαλούμενων
μαθηματικώς δημιουργούμενων σχημάτων και
εικόνων, δηλαδή σχημάτων ή εικόνων που
παράγονται από Η/Υ με την κατάλληλη
εφαρμογή κάποιων μαθηματικών τύπων ή
αλγορίθμων. Παράδειγμα τέτοιων σχημάτων με
μεγάλη αισθητική απήχηση αποτελεί το
σύνολο Mandelbrot,
το οποίο προέρχεται από την επαναληπτική
διαδικασία επανεισαγωγής των τιμών στη
συνάρτηση ![]() ,
όπου το z
είναι μιγαδική μεταβλητή που ξεκινάει από
το 0 και το c
ένας τυχαίος μιγαδικός σταθερός αριθμός
που αντιπροσωπεύει το σημείο του επιπέδου
που εξετάζεται. Όταν αναπαρασταθεί στην
οθόνη ενός υπολογιστή το σύνολο αυτό, δίνει
την εικόνα μιας καρδιάς με οίδημα ([8]).
,
όπου το z
είναι μιγαδική μεταβλητή που ξεκινάει από
το 0 και το c
ένας τυχαίος μιγαδικός σταθερός αριθμός
που αντιπροσωπεύει το σημείο του επιπέδου
που εξετάζεται. Όταν αναπαρασταθεί στην
οθόνη ενός υπολογιστή το σύνολο αυτό, δίνει
την εικόνα μιας καρδιάς με οίδημα ([8]).
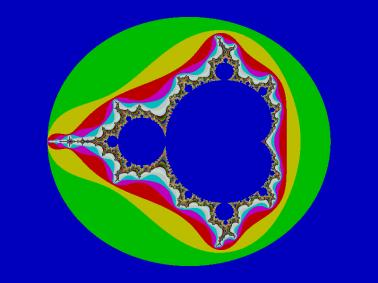
Σύνολο Mandelbrot
Δεν υπάρχει πιστεύουμε αμφιβολία ότι οι εικόνες που δημιουργούνται με μαθηματικό τρόπο μπορεί να θεωρηθούν ως έργα τέχνης, όπως ακριβώς και οι εικόνες ή τα σχήματα που παράγονται με χρήση άλλων μεθόδων και μέσων, όπως λόγου χάρη τη φωτογραφική μηχανή. Με την έννοια αυτή τα μαθηματικά μετατρέπονται σε ένα επιπλέον μέσο – εργαλείο του κόσμου της τέχνης. Ακριβώς, βέβαια, όπως όλες οι φωτογραφίες δεν αποτελούν τέχνη, το ίδιο και όλες οι μαθηματικές εικόνες δεν θα πρέπει να θεωρούνται έργα τέχνης.
Ίσως οι καθοριστικές πλευρές που μπορεί να κρίνουν και σ’ αυτή την περίπτωση ένα έργο τέχνης είναι η πρόθεση του δημιουργού της εικόνας, ο βαθμός συμμετοχής του στην επεξεργασία της εικόνας και εάν το περιεχόμενο της εικόνας έχει κάτι σημαντικό να πει. Τα έργα τέχνης πάντως που δημιουργούνται με μαθηματικό τρόπο και ιδιαίτερα με την βοήθεια της τεχνολογίας, διαφέρουν από άλλες μορφές τέχνης επειδή, από την φύση τους, ενθαρρύνουν μια επικοινωνία και καλλιεργούν μια γόνιμη διασταύρωση μεταξύ τέχνης και επιστήμης. Το βασίλειο της μαθηματικής τέχνης σήμερα είναι πολύ πιο ευρύ και ποικίλο απ’ ότι πιστεύουν οι περισσότεροι άνθρωποι. Ένας εντυπωσιακός αριθμός σύγχρονων καλλιτεχνών χρησιμοποιούν τα μαθηματικά – από τους αριθμούς Fibonacci και τα ψηφία του π μέχρι υπερστερεά, πολύτοπα και ταινίες Möbious – ως πηγή έμπνευσης για τις δημιουργίες τους.
Ένας από τους ευρύτερους σκοπούς της διδασκαλίας της γεωμετρίας στη Δ/θμια εκπαίδευση είναι να προσφέρει μια ευκαιρία στους μαθητές να βιώσουν τη δημιουργική αλληλεπίδραση μεταξύ μαθηματικών και τέχνης [8]. Το εκπαιδευτικό δυναμικό γεωμετρικό λογισμικό που διατίθεται σήμερα με τους δύο κύριους εκπροσώπους του, το Cabri και το Sketchpad ([3], [11]), προσφέρει τη δυνατότητα καλλιτεχνικών μαθηματικών δημιουργιών χάρη κυρίως στα μενού των γεωμετρικών μετασχηματισμών που τα προγράμματα αυτά διαθέτουν. Ξεκινώντας από ειδικά σχήματα και κάνοντας χρήση των ειδικών εργαλείων της μεταφοράς, της ανάκλασης και της περιστροφής είναι δυνατόν να δημιουργηθούν εκπληκτικά σχήματα στην οθόνη του Η/Υ που εντυπωσιάζουν τον θεατή και ανάλογα κατατάσσονται ως έργα τέχνης σε μια αξιολογική πυραμίδα.
Παρακάτω θα παρουσιάσουμε κάποιες ιδέες για τη δημιουργία ψηφιδωτών διαφόρων τύπων με χρήση των δυνατοτήτων του Sketchpad και κυρίως των εργαλείων γεωμετρικών μετασχηματισμών. Οι ιδέες αυτές είναι δυνατόν να αξιοποιηθούν ως βάση για την ανάθεση Projects και συνθετικών δημιουργικών εργασιών στα πλαίσια διδασκαλίας του μαθήματος της γεωμετρίας στο Γυμνάσιο ή το Λύκειο.
Με τον όρο ψηφιδωτό ή πλακόστρωση εννοούμε μια διευθέτηση κλειστών σχημάτων, τα οποία καλύπτουν πλήρως το επίπεδο, χωρίς επικαλύψεις ή χάσματα ([6], [9]).
1.Ψηφιδωτά – πλακοστρώσεις με ένα κανονικό πολύγωνο (καθαρά κανονικά
ψηφιδωτά).
Υπάρχουν τρία κανονικά πολύγωνα με τα οποία μπορεί να καλυφθεί το επίπεδο: το ισόπλευρο τρίγωνο, το τετράγωνο και το κανονικό εξάγωνο. Από έτοιμα ήδη αρχεία εντολών του Sketchpad (Script) διαλέγουμε ένα απ’ αυτά τα κανονικά πολύγωνα ,π.χ. το κανονικό εξάγωνο, και το σχεδιάζουμε. Με παράλληλες μετατοπίσεις κατά διάνυσμα ίσο με το διάνυσμα μιας διαγωνίου μετατοπίζουμε το αρχικό πολύγωνο πρώτα οριζόντια και μετά διαγώνια προς τα κάτω, μέχρις ότου καλύψουμε το παράθυρο σχεδιασμού. Χρωματίζοντας κατάλληλα το εσωτερικό αυτού του πολύγωνου έχουμε ένα ωραίο αποτέλεσμα, όπως δείχνει το παρακάτω παράδειγμα.
![]()

Οριζόντια μετατόπιση κατά το διάνυσμα ΑΒ και μετά κατά διάνυσμα ΒΓ

Τέλος χρωματίζουμε όπως θέλουμε
2.Ψηφιδωτά με περισσότερα πολύγωνα (ημικαθαρά κανονικά ψηφιδωτά).
Υπάρχουν οκτώ τύποι ημικαθαρών κανονικών ψηφιδωτών, όπως φαίνονται στο παρακάτω σχήμα
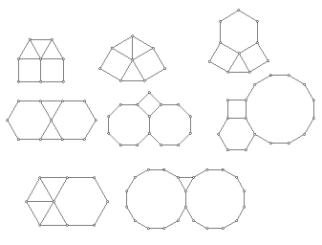
Μπορούμε να ξεκινήσουμε, για παράδειγμα, από ένα κανονικό εξάγωνο και να κατασκευάσουμε ισόπλευρα τρίγωνα ή τετράγωνα σε κάθε πλευρά του κανονικού εξαγώνου. Κατόπιν εκτελούμε παράλληλες μετατοπίσεις αυτού του σχήματος χρωματίζοντας κατάλληλα το εσωτερικό αυτών των πολυγώνων, όπως στα παρακάτω παραδείγματα.

3. Μη κανονικά ψηφιδωτά τύπου Escher.
α) Έναρξη από ένα ισόπλευρο τρίγωνο.
|
Σε ένα ισόπλευρο τρίγωνο κατασκευάζουμε μια τεθλασμένη γραμμή από την μια κορυφή μέχρι το μέσο της πλευράς. |
|
|
Περιστρέφουμε την τεθλασμένη γραμμή κατά 180ο γύρω από το μέσο της πλευράς. |
|
|
Περιστρέφουμε και τις δύο τεθλασμένες γύρω από την κορυφή Α κατά 60ο, και την νέα που προκύπτει από τη περιστροφή πάλι γύρω από την κορυφή Β |
|
|
Κατασκευάζουμε το εσωτερικό του πολυγώνου και το χρωματίζουμε |
|
|
Στη συνέχεια με διαδοχικές περιστροφές του πολυγώνου γύρω από την κορυφή Β κατά 60ο θα φθάσουμε στο παρακάτω σχήμα |
|

β) Έναρξη από ένα τετράγωνο
|
Σχεδιάζουμε δυο τεθλασμένες γραμμές ανάμεσα σε δυο διαδοχικές κορυφές ενός τετραγώνου |
|
|
Μεταφέρουμε την μια οριζόντια και την άλλη κατακόρυφα κατά διάνυσμα ίσο με την πλευρά του τετραγώνου. |
|
|
Κατασκευάζουμε το πολύγωνο που ορίζεται από τις κορυφές της πολυγωνικής γραμμής και χρωματίζουμε. |
|
|
Μεταφέρουμε το πολύγωνο οριζόντια κατά διάνυσμα ίση με την πλευρά του τετραγώνου όσες φορές θέλουμε. Κάνουμε το ίδιο κατακόρυφα και θα καταλήξουμε στο παρακάτω σχήμα
|
|

Με παρόμοιο τρόπο, χρησιμοποιώντας ανακλάσεις, περιστροφές και μεταφορές πάνω σε ένα σχήμα – βάση μπορούμε να δημιουργήσουμε τα παρακάτω σχήματα.
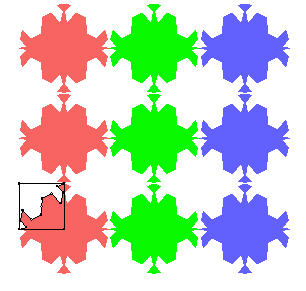
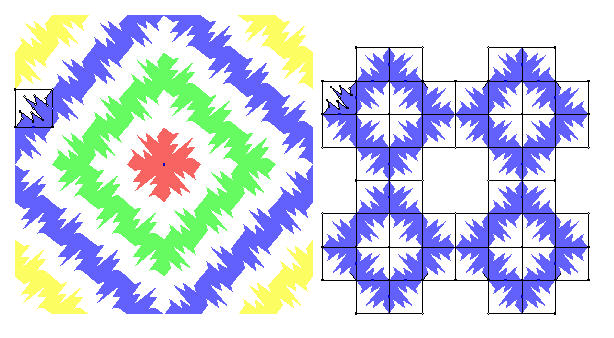
γ) Έναρξη από ένα παραλληλόγραμμο
|
Σχεδιάζουμε δύο τεθλασμένες γραμμές ανάμεσα σε δύο διαδοχικές κορυφές ενός παραλληλογράμμου |
|
|
Μεταφέρουμε την μια κατά διάνυσμα ΑΒ και την άλλη κατά διάνυσμα ΓΑ. |
|
|
Κατασκευάζουμε το πολύγωνο που ορίζεται από τις κορυφές της πολυγωνικής γραμμής και χρωματίζουμε. |
|
|
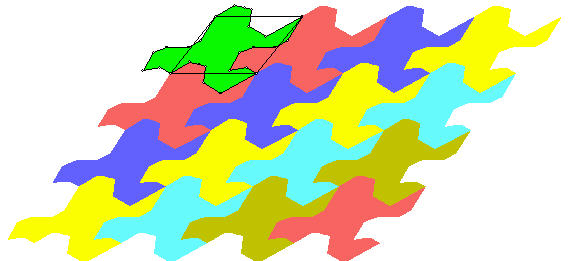
Μεταφέρουμε αρχικά οριζόντια κατά διάνυσμα ΑΒ όσες φορές θέλουμε και μετά κατά διάνυσμα ΓΑ. Έτσι θα φθάσουμε στο παρακάτω σχήμα |
|
|
Σχεδιάζουμε μια τεθλασμένη από την κορυφή μέχρι το σημείο τομής των διαγωνίων του παραλληλογράμμου |
|
|
Περιστρέφουμε την τεθλασμένη κατά 180ο γύρω από το σημείο τομής των διαγωνίων και στη συνέχεια ορίζουμε το πολύγωνο. Κάνουμε το ίδιο και για το άλλο πολύγωνο |
|
|
Ανακλούμε και τα δύο πολύγωνα κατά την πλευρά ΑΒ. Στην συνέχεια μεταφέρουμε οριζόντια κατά διάνυσμα ΑΒ όσες φορές θέλουμε και μετά κατά -2 (απόσταση του Γ από την ΑΒ) πάλι όσες φορές θέλουμε. Έτσι θα φθάσουμε στο παρακάτω σχήμα
|
|

δ) Έναρξη από ένα κανονικό εξάγωνο
|
Στην πλευρά ενός κανονικού εξαγώνου κατασκευάζουμε μια τεθλασμένη γραμμή. |
|
|
Περιστρέφουμε την τεθλασμένη κατά 120ο από την επιλεγμένη κορυφή. |
|
|
Επαναλαμβάνοντας την διαδικασία φθάνουμε στο σχήμα |
|
|
Κατασκευάζουμε το πολύγωνο που ορίζεται από την τεθλασμένη γραμμή |
|
|
Επιλέγουμε το πολύγωνο και το περιστρέφουμε κατά 120ο γύρω από την μια κορυφή του εξαγώνου Επαναλαμβάνοντας το ίδιο για όλες τις κορυφές παίρνουμε το παρακάτω σχήμα |
|
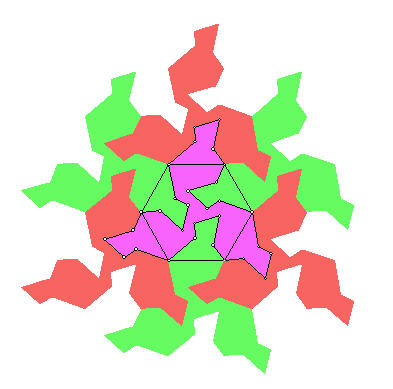
Παρόμοια, ξεκινώντας από διάφορα άλλα γεωμετρικά σχήματα και εφαρμόζοντας παραπλήσιες τεχνικές μπορούμε να δημιουργήσουμε ανάλογες διακοσμητικές εικόνες. Εάν κατορθώσουμε να δημιουργήσουμε τις εικόνες με τέτοιο τρόπο ώστε να παριστάνουν κάποιο θέμα, τότε σίγουρα θα μπορούμε να μιλάμε για έργο τέχνης.
ΒΙΒΛΙΟΓΡΑΦΙΚΕΣ ΑΝΑΦΟΡΕΣ
[1] Bool,F., Locher,J. and Wierda, F.: M.C.Escher-His Life and Complete
Graphic Work, New York, H. Abrams, 1982.
[2] Bunt, L., Jones, P., Bedient,J.: Οι ιστορικές ρίζες των στοιχειωδών
μαθηματικών, Αθήνα, Γ. Πνευματικός, 1981.
[3] Cabri Geometry, Texas Instruments, Dalas,Texas, 1994 ( Ελληνική έκδοση: Εκδόσεις Καστανιώτη Α.Ε., 2001).
[4] Ernst, B.: The Magic Mirror of M.C. Escher, New York, Ballantine,
1976.
[5] Gillings, R.: Mathematics in the Time of Pharaohs, Cambridge, Mass.,
The MIT Press, 1972.
[6] Grunbaum,B.& Shepard,G.: Tilings and Patterns, New York,
W.H.Freeman and Company, 1986.
[7] Mandelbrot, B.: Fractals and an Art for the Sake of Science, In The
Visual mind, ed. By Michele Emmer, Cambridge, MIT Press, 1993.
[8] National Standards for School Mathematics, National Council of
Teachers of Mathematics, Reston, Virginia, 1990.
[9] Seymour, D.& Britton, J.: Introduction to Tessellations, Dale Seymour
Publications, 1989.
[10] Struik,D.: Συνοπτική Ιστορία των Μαθηματικών, Αθήνα,
Ι.Ζαχαρόπουλος, 1982.
[11] The Geometer’s Sketchpad, Key Curriculum Press, Berkeley,
California,1995 (Ελληνική έκδοση: Καστανιώτης, Αθήνα, 2000).
[12] Φίλη Χ.: Γεωμετρία και Τέχνη: Δυο παράλληλες αναζητήσεις,
Πρακτικά του 17ου Πανελληνίου Συνεδρίου Μαθηματικής Παιδείας,
Ε.Μ.Ε., 2000.
In this paper we first discuss some aspects of mathematical art. Although mathematics and art are two seemingly disparate fields according to contemporary views, there are a number of visual artists who make mathematics a focus of their work and there are several themes that have been widely used by mathematical artist. These include polyedra, tessellations, impossible figures, Möbious bands, unusual perspective systems and fractals. Afterwards we offer some ideas and suggestions for the construction of several types of tessellations using several Sketchpad commands such as script, translate, rotate and reflect. All these ideas can be used to help students to create their own tessellations using the Geometer’s Sketchpad.