
Τα μαθηματικά από αρχαιοτάτων χρόνων αποτελούν ένα από τα βασικότερα συστατικά και ένα διαχρονικό παράγοντα του πολιτισμού μας. Γι’ αυτό εξάλλου επέζησαν χιλιάδες χρόνια και εξακολουθούν να βρίσκονται στο επίκεντρο του σύγχρονου πολιτισμού μας. Για τα στοιχεία του Ευκλείδη, το μνημειώδες αυτό έργο του μεγάλου γεωμέτρη της αρχαιότητας, το οποίο επηρέασε όλες σχεδόν τις επιστήμες, έχουν καταγραφεί πάνω από 1000 διαφορετικές εκδόσεις και είναι το δεύτερο σε συνολικό αριθμό αντιτύπων μετά τη Βίβλο.
Θα υπενθυμίσουμε ότι το έτος 2000 είχε ανακηρυχθεί διεθνώς ως έτος των μαθηματικών από την παγκόσμια μαθηματική κοινότητα. Η επιλογή του συγκεκριμένου έτους σηματοδοτεί τη σπουδαιότητα των μαθηματικών στη σύγχρονη κοινωνία και καθορίζει τη σημασία τους για την τρίτη χιλιετία που διανύει η ανθρωπότητα.
Η εποχή μας χαρακτηρίζεται ως η τεχνολογική εποχή της επανάστασης της γνώσης και της πληροφορίας. Η ζωή μας γίνεται συνεχώς πιο πολύπλοκη και πιο απαιτητική για το ανθρώπινο μυαλό, αφού ο κλοιός των τεχνολογικών μέσων που μας περιβάλλει απαιτεί αυξημένες νοητικές λειτουργίες σε καθημερινό επίπεδο και ταυτόχρονα κατανάλωση μικρότερης μυϊκής δύναμης. Τα μαθηματικά θεωρούνται ιδανικά στο να καλλιεργήσουν την απαιτούμενη ορθολογιστική και γρήγορη σκέψη, αλλά και απαραίτητα ως το βασικό υπόβαθρο για την κατάκτηση της γνώσης και σημαντικότερο εφόδιο για επαγγελματική κατάρτιση.
Αν ρίξουμε μια ματιά γύρω μας στα πράγματα που μας περιβάλλουν, καθώς και στις δραστηριότητες που λαμβάνουν χώρα και έχουμε διάθεση να στοχαστούμε λιγάκι, θα διαπιστώσουμε ότι πίσω από κάθε τι κρύβονται τα μαθηματικά. Από οικοδομές και άλλου τύπου κατασκευές μέχρι τις οικιακές συσκευές και τη μουσική, τα μαθηματικά είναι υπεύθυνα για το τελικό αποτέλεσμα που βλέπουμε ή ακούμε. Ο μεγάλος μαθηματικός Leibnitz ισχυρίστηκε ότι η απόλαυση που νιώθει κανείς ακούγοντας μουσική προέρχεται από το μέτρημα που καθορίζει το μουσικό ρυθμό. Η μουσική, είπε, δεν είναι τίποτε άλλο παρά μια ασυνείδητη αριθμητική.
Όσο η ανάγκη για εμβάθυνση και κατανόηση του φυσικού αλλά και του κοινωνικοπολιτικού – οικονομικού περιβάλλοντος αυξάνει, τόσο οι απαιτήσεις για οργανωμένη μαθηματική σκέψη γίνονται πιο επιτακτικές. Αν κάποιος ανατρέξει σε κοινωνικοοικονομικά άρθρα και αναλύσεις, που δημοσιεύονται αθρόα αυτήν την εποχή με την ευκαιρία της αλλαγής του αιώνα, θα εντοπίσει ένα κοινό χαρακτηριστικό, ότι δηλαδή στον αιώνα που ήρθε η παραγωγή προϊόντων, που σφράγισε τον αιώνα που έφυγε, θα αντικατασταθεί με την ταχύτατη παροχή γνώσης και πληροφορίας. Οι οικονομολόγοι εκτιμούν ότι μέχρι το 2020 το 80% των θέσεων εργασίας σ’ ολόκληρο τον κόσμο θα αφορά άμεση ή έμμεση παροχή γνώσης και πληροφορίας και μόνο το 20% θα αφορά παραγωγή προϊόντων και αγαθών. Όλες αυτές οι εκτιμήσεις μας δείχνουν ένα ξεκάθαρο δρόμο για το μέλλον των μαθηματικών. Ένα δρόμο που αφορά τις άπειρες δυνατότητες και ευκαιρίες για όσους έχουν μάτια και βλέπουν τι συμβαίνει γύρω μας.
Αυτή η διαπίστωση δείχνει, με τη σειρά της ,την αξία της σωστής μαθηματικής εκπαίδευσης για το μέλλον της κοινωνίας μας. Επιτακτική είναι λοιπόν η ανάγκη όλοι οι μαθητές να μάθουν μαθηματικά γιατί έτσι τους ανοίγεται μια πόρτα που οδηγεί στην επιτυχημένη επαγγελματική – κοινωνική και οικογενειακή ζωή. Τα σχολικά μαθηματικά πρέπει να είναι υψηλής ποιότητας και να προκαλούν όλους τους μαθητές. Γονείς και μαθητές θα πρέπει να συνειδητοποιήσουν ότι η επιτυχία στο μάθημα των μαθηματικών δεν εξαρτάται από μια ιδιοτροπία της φύσης, όπως π.χ. το έμφυτο ταλέντο, αλλά βασίζεται κυρίως στη σκληρή προσπάθεια και ενασχόληση με το αντικείμενο, όπως εξάλλου και η κατάκτηση οποιασδήποτε δεξιότητας.
Εδώ όμως αρχίζει να διαφαίνεται η μεγάλη αντίθεση της εποχής μας: Ενώ, δηλαδή, η αξία της μαθηματικής επιστήμης και μαθηματικής εκπαίδευσης ολοένα μεγαλώνει, οι περισσότεροι άνθρωποι (παιδιά και ενήλικες) θεωρούν ότι το μάθημα των μαθηματικών αποτελεί τον πιο φοβερό εφιάλτη στα όνειρά τους.
Το συναίσθημα της μαθηματικοφοβίας.
Οι στάσεις και τα συναισθήματα που διαμορφώνουν οι μαθητές για τα μαθηματικά επηρεάζουν καθοριστικά την όλη διαδικασία διδασκαλίας – μάθησης (Zaslavsky, 1994). Μια από τις πιο διαδεδομένες απόψεις γύρω από το μάθημα των μαθηματικών είναι αυτή που αφορά στη δυσκολία και το αίσθημα δυσφορίας ή απέχθειας που αυτό προκαλεί. Ένα, επίσης, από τα πιο συνηθισμένα συναισθήματα των μαθητών σχετικά με τα μαθηματικά, το οποίο επιδρά αρνητικά στις επιδόσεις τους, είναι η λεγόμενη μαθηματικοφοβία. Με τον όρο αυτό εννοείται η δυσφορία, η ένταση, η ανησυχία, το άγχος και τελικά ο φόβος που νιώθουν τα παιδιά όταν ασχολούνται με το μαθηματικό αντικείμενο (Richardson & Suinn, 1972 . Tobias, 1993).
H μαθηματικοφοβία έχει ως αποτέλεσμα τη μείωση, αρχικά, της αυτοπεποίθησης των μαθητών και στη συνέχεια των επιδόσεών τους στα μαθηματικά, αφού ο φόβος τους παραλύει τη σκέψη. Οι φτωχές επιδόσεις, με τη σειρά τους, αυξάνουν το δέος και το φόβο των παιδιών για το μαθηματικό αντικείμενο. Δημιουργείται, έτσι, ένας φαύλος κύκλος, ο οποίος αν δεν αντιμετωπιστεί εγκαίρως δεν θα σταματήσει ποτέ να υπάρχει και να απειλεί μεγάλες ομάδες του μαθητικού πληθυσμού.
Το γεγονός ότι η μαθηματικοφοβία απειλεί τόσο τη συμμετοχή των παιδιών στο μάθημα των μαθηματικών όσο και την επίδοσή τους, αλλά και η διαπίστωση ότι αποτελεί ένα ευρέως διαδεδομένο φαινόμενο, καθιστά τη μελέτη της εξαιρετικής σημασίας ( Grouws,1992 . Skiba,1990).
H άποψη αυτή ενισχύεται παραπέρα από το γεγονός ότι τα μαθηματικά γίνονται όλο και πιο απαραίτητα στη ζωή μας, καθώς η τεχνολογική επανάσταση έχει δημιουργήσει ένα περιβάλλον όπου τα άτομα που έχουν δυσκολίες με τις μαθηματικές έννοιες θα αποκλείονται σταδιακά από όλο και περισσότερες σημαντικές θέσεις στην αγορά εργασίας και κινδυνεύουν έτσι να περιθωριοποιηθούν κοινωνικά Με την έννοια αυτή, ο μαθηματικός αλφαβητισμός και η μαθηματική εκπαίδευση είναι στην ουσία ένα ζήτημα πολιτικών δικαιωμάτων, αφού τα παιδιά που δεν είναι επαρκώς εφοδιασμένα με μαθηματικές δεξιότητες και γνώσεις κινδυνεύουν να καταδικαστούν σε πολίτες δεύτερης κατηγορίας που συνιστούν τα μέλη μιας οικονομικά υποβαθμισμένης κοινωνικής τάξης (Moses, 2001).
Σήμερα είναι εδραιωμένη όσο ποτέ η άποψη ότι τα μαθηματικά συνιστούν ένα κρίσιμο κοινωνικό φίλτρο, το οποίο καθορίζει τις επαγγελματικές δραστηριότητες των ατόμων και σε μεγάλο βαθμό την επαγγελματική, προσωπική και οικογενειακή τους ευτυχία (Schoenfeld, 2002).
Τα βασικότερα αίτια της μαθηματικοφοβίας.
Η μαθηματικοφοβία δεν αποτελεί πρόβλημα που οφείλεται σε παθολογικούς παράγοντες, όπως η δυσλεξία, ή η δυσαριθμησία, αλλά έχει κυρίως εξωτερικά αίτια και προκαλείται από τις οποιεσδήποτε αρνητικές – τραυματικές εμπειρίες των μαθητών με τα μαθηματικά. Η μαθηματικοφοβία συνιστά ένα πολύπλοκο φαινόμενο και είναι το αποτέλεσμα πολλών παραγόντων, οι οποίοι επηρεάζουν όλο το φάσμα της διδασκαλίας – μάθησης των μαθηματικών. Παρακάτω θα αναφέρουμε κάποιους από τους, διαπιστωμένους μέσω ερευνών, παράγοντες οι οποίοι ευθύνονται για τα αρνητικά συναισθήματα της μαθηματικοφοβίας και αποτελούν τις πιθανότερες αιτίες που την προκαλούν (Buxton, 1981 . Gliner, 1987 . Greenwood, 1984. Hembree, 1990 . Michell & Collins, 1991 . Wigfield & Meece, 1988). Βεβαίως, δεν θα αναφερθούμε καθόλου σε αίτια που αποδίδονται σε νοητικές δυσλειτουργίες, όπως π.χ. μνήμη μικρής χωρητικότητας, δυσκολία στη λεκτική ικανότητα, δυσλειτουργία του εγκεφάλου, έλλειψη συντονισμού μεταξύ δεξιού και αριστερού εγκεφαλικού ημισφαιρίου κ.λπ.
Όπως προκύπτει από σχετικές έρευνες στη διδακτική των μαθηματικών, αναφορικά με τα αίτια του φαινομένου της μαθηματικοφοβίας, ο παράγοντας ο οποίος βαρύνει περισσότερο στη δημιουργία του φαινομένου αυτού είναι το διδακτικό στυλ και η διδακτική προσέγγιση που ακολουθεί ο δάσκαλος μέσα στην τάξη (Greenwood, 1984 . Grouws, 1993 . Jackson & Leffingwell, 1999). Oι δάσκαλοι μπορεί να διαμορφώσουν τις προϋποθέσεις ενός κλίματος ιδανικού για την καλλιέργεια της μαθηματικοφοβίας μέσα από τις καθημερινές πρακτικές που υιοθετούν στην τάξη: Υπερβολική έμφαση στην απομνημόνευση κανόνων και αλγορίθμων, φορμαλιστική παρουσίαση περιεχομένου, υπερβολική έμφαση στην μαθηματική αυστηρότητα και αποδεικτική διαδικασία, ψυχρή – φορμαλιστική αξιολόγηση, έλλειψη επικοινωνίας με τους μαθητές, μη ενεργοποίηση και συμμετοχή των μαθητών στην οικοδόμηση της μαθηματικής γνώσης κ.λπ.
Αν και τα μαθηματικά ενδιαφέρονται κατά κύριο λόγο για τις σωστές απαντήσεις και τα σωστά αποτελέσματα, οι στόχοι αυτοί μπορούν να επιτευχθούν και με τη βοήθεια ανοιχτών προβλημάτων, μέσω διδακτικών προσεγγίσεων οι οποίες δίνουν την ευκαιρία στους μαθητές να νιώσουν την εμπειρία ολόκληρου του φάσματος της μαθηματικής δημιουργίας και ανακάλυψης. Αντί να αποστηθίζουν μαθηματικές μεθόδους, κανόνες και αλγορίθμους, οι μαθητές χρειάζονται να αποκτήσουν ικανότητες να πειραματίζονται, να εικάζουν, να αναλύουν, να αμφισβητούν, να ελέγχουν και να βρίσκουν λύσεις. Ικανότητες, δηλαδή, οι οποίες μπορεί να εφαρμοστούν αργότερα σε διαφορετικές καταστάσεις και πλαίσια αναφοράς.
Αλλά πώς θα γίνει αυτή η αλλαγή; Ποιες διδακτικές μέθοδοι ή προσεγγίσεις είναι σε θέση να φέρουν σε επαφή τα μαθηματικά με το σύνολο του μαθηματικού πληθυσμού και να τα κάνουν ενδιαφέροντα και ελκυστικά; Αρκετές έρευνες προσπάθησαν να ερευνήσουν τις αιτίες της μαθηματικοφοβίας και την αξία που μπορεί να έχουν εναλλακτικές διδακτικές τεχνικές και στρατηγικές στην αντιμετώπιση αυτού του προβλήματος (Norwood, 1994 . Resek & Rupley, 1980, Spikell, 1993).
Στη συνέχεια, με βάση τη σχετική έρευνα, απευθυνόμαστε στο δάσκαλο των μαθηματικών και προτείνουμε κάποιους τρόπους, οι οποίοι θα τον βοηθήσουν να οικοδομήσει ένα ασφαλές και υποστηρικτικό περιβάλλον, στο οποίο οι μαθητές θα απολαμβάνουν τη μάθηση χωρίς να φοβούνται την αποτυχία και θα αποκτήσουν θετικές στάσεις απέναντι στα μαθηματικά.
Διδακτικές στρατηγικές για την αντιμετώπιση της μαθηματικοφοβίας.
· Μη δυσανασχετήσεις εάν κάποιο παιδί δεν καταλαβαίνει κάτι ή κάνει κάποιο λάθος. Ας του δώσουμε να καταλάβει ότι τα λάθη δεν είναι κατάρα όταν μαθαίνουμε απ’ αυτά.
· Προσπάθησε να βοηθήσεις το παιδί να ξανασκεφτεί και να προσπαθήσει ξανά.
· Μίλησε στην τάξη για φημισμένους επιστήμονες, οι οποίοι τολμούσαν να εφαρμόζουν νέες ιδέες και δεν φοβόντουσαν μήπως κάνουν λάθη (Voolich, 1993 . Bell,1986).
· Χρησιμοποίησε τεχνικές για να ενθαρρύνεις τους μαθητές να μετατρέψουν τις λανθασμένες απαντήσεις σε σωστές.
· Μην επιτρέψεις στους άλλους μαθητές της τάξης να σχολιάσουν αρνητικά όταν κάποιος συμμαθητής τους κάνει κάποιο λάθος.
· Δημιούργησε προϋποθέσεις επιτυχίας στους μαθητές.
· Επέτρεψε στους μαθητές να συνειδητοποιήσουν ότι μπορούν να επιτύχουν με τις δικές τους δυνάμεις.
· Επιβράβευσε την κάθε προσπάθεια.
· Δώσε αρκετό χρόνο στους μαθητές να τελειώσουν την εργασία τους.
· Άφησε τους μαθητές να καταλάβουν ότι πιστεύεις πως μπορούν να επιτύχουν.
· Χρησιμοποίησε ομαδο-συνεργατικές στρατηγικές, χωρίζοντας την τάξη σε ετερογενείς ομάδες.
· Δημιούργησε μια ισορροπία μεταξύ συνεργατικών και συναγωνιστικών τρόπων μάθησης.
· Ενθάρρυνε τη συμμετοχή όλων των μελών στην εργασία της ομάδας.
· Χρησιμοποίησε εκπαιδευτικό υλικό για τη μετάβαση από το συγκεκριμένο στο αφηρημένο.
· Ενθάρρυνε τις διαφορετικές στρατηγικές για την προσέγγιση και επίλυση προβλημάτων.
· Μην ενθαρρύνεις τα γρήγορα και εύκολα κέρδη.
· Εφοδίασε τους μαθητές με ένα πλήθος στρατηγικών-τεχνικών για την επίλυση προβλημάτων διαφόρων τύπων.
· Προώθησε την επιθυμία για επιμονή μέχρι την τελική επιτυχία. Δώσε στους μαθητές να καταλάβουν ότι δεν είναι δυνατόν όλα τα προβλήματα να λυθούν σε 5 – 10 λεπτά.
· Βοήθησε τους μαθητές να παίρνουν σωστές αποφάσεις για το πότε θα πρέπει να συνεχίζουν να επιμένουν σε κάποιο τρόπο λύσης και πότε πρέπει να σταματούν και να δοκιμάζουν κάτι άλλο.
· Ενθάρρυνε τους μαθητές να προσεγγίζουν το πρόβλημα με πολλούς και διαφορετικούς τρόπους. Μια τακτική, η οποία χρησιμοποιείται συχνά από επίμονους λύτες προβλημάτων και οδηγεί σε επιτυχία, είναι η εξής:
|
· Ζήτησε από τους μαθητές που συναντούν δυσκολίες να ξαναδιατυπώσουν το πρόβλημα με δικά τους λόγια, προκειμένου να εντοπιστούν οι πιθανές παρανοήσεις.
· Έλεγξε εάν οι μαθητές γνωρίζουν τη σημασία ειδικών λέξεων ή φράσεων.
· Δώσε στους μαθητές, εάν το κρίνεις αναγκαίο, μια μικρή υπόδειξη, η οποία θα τους βοηθήσει να «ξεμπλοκάρουν».
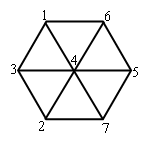
Πρόβλημα: Στις κορυφές του παρακάτω κανονικού εξαγώνου και στο κέντρο
του, τοποθέτησε τους αριθμούς 1,2,3,4,5,6,7 έτσι ώστε τα
αθροίσματα των αριθμών αυτών κατά μήκος των τριών διαγωνίων
να είναι ίσα.

Στην αρχή, οι μαθητές μπορεί να τοποθετούν τους αριθμούς στην τύχη, προσπαθώντας να ικανοποιήσουν την απαίτηση του προβλήματος. Δοκιμάζουν διάφορους συνδυασμούς μέχρις ότου επιτύχουν τα αθροίσματα στις τρεις διαγώνιους να είναι ίσα. Αυτό μπορεί να τους πάρει πολύ χρόνο και είναι αμφίβολο αν θα τα καταφέρουν στο τέλος.
Αφού τους αφήσουμε να δοκιμάσουν αρκετές φορές, διακόπτουμε τις προσπάθειες και τους υποδεικνύουμε ότι είναι καιρός να αλλάξουν τακτική και να προσεγγίσουν το πρόβλημα με διαφορετικό τρόπο.
- Δοκίμασε να πετύχεις ένα συνολικό άθροισμα, π.χ. 13 κατά μήκος κάθε
διαγωνίου.
- Εάν αποτύχεις δοκίμασε μια άλλη ιδέα να τοποθετήσεις στο κέντρο το μεσαίο
αριθμό, το 4. Προσπάθησε στη συνέχεια να βρεις ποιους άλλους αριθμούς θα
βάλεις στις κορυφές.
- Δοκίμασε τους δυο ακραίους 1 και 7. Τότε το άθροισμα είναι 1+4+7=12.
- Μήπως η ίδια τεχνική εφαρμόζεται και για τους αριθμούς που απέμειναν;
Πράγματι, 2+4+6=12 και 3+4+5=12. άρα η λύση είναι:
Τελειώνοντας, θα λέγαμε ότι η μαθηματικοφοβία είναι ένα ευρέως διαδεδομένο φαινόμενο, το οποίο συνιστά ένα απειλητικό για την κοινωνία πρόβλημα. Κατά το μεγαλύτερο ποσοστό δημιουργείται στις τάξεις των μαθηματικών και οφείλεται κυρίως στην προβληματική διδασκαλία και συμπεριφορά των διδασκόντων. Την εποχή στην οποία ζούμε, οι ανάγκες της κοινωνίας απαιτούν περισσότερες μαθηματικές γνώσεις και νοητικές δεξιότητες. Τα μαθηματικά πρέπει να γίνουν προσιτά και ελκυστικά για όλο το μαθητικό πληθυσμό έτσι ώστε να μειωθεί η μαθηματικοφοβία, η οποία εμποδίζει τη συμμετοχή σε μαθηματικές δραστηριότητες.
Επομένως, οι δάσκαλοι των μαθηματικών οφείλουν να επανεξετάσουν τις παραδοσιακές διδακτικές μεθόδους και πρακτικές, οι οποίες δεν λαμβάνουν συνήθως υπόψη τις διαφορετικές ανάγκες και ιδιαιτερότητες των μαθητών. Το μάθημα πρέπει να παρουσιάζεται με διαφορετικούς κάθε φορά τρόπους και να προσεγγίζεται με διαφορετικές κάθε φορά στρατηγικές. Για παράδειγμα, μια νέα έννοια μπορεί να διδαχθεί μέσω ανακαλυπτικών προσεγγίσεων, συνεργατικής μάθησης, χειρισμού συγκεκριμένου εκπαιδευτικού υλικού, οπτικών βοηθημάτων και χρήση της σύγχρονης τεχνολογίας. Ο στόχος μας πρέπει να είναι να οικοδομήσουμε ένα υποστηρικτικό περιβάλλον ασφάλειας, ενεργητικής συμμετοχής και προσπάθειας, το οποίο θα βοηθήσει τους μαθητές να μάθουν και να απολαύσουν την περιπέτεια και τη μαγεία της μαθηματικής δημιουργίας.
Bell, E.T. (1986). Men of mathematics. New York: Simon & Shuster.
Buxton, L. (1981). Do you panic about maths? Coping with maths anxiety. London:
Heinemann Educational Books Ltd.
Gliner, G. S. (1987). The relationship between mathematics anxiety and achievement
variables. School Science and Mathematics, 87, 81-87.
Greenwood, J. (1984). My anxiety about math anxiety. Mathematics Teacher, 77,
662-663.
Grouws R.(Ed.) (1992). Handbook of Research on Mathematics Teaching and
Learning. Macmillan Publishing Co., London, 575-596.
Hembree, R. (1990). The Nature, Effects and Relief of Mathematics Anxiety. Journal
for Research in Mathematics Education, 21, 33-46.
Jackson, C. D. & Leffinguell, R. J. (1999). The role of instructors in creating math
anxiety in students from kindergarten through college. Mathematics Teacher, 92,
583-586.
Mitchell, C. and Collins, L. (1991). Math anxiety. What it is and what to do about it.
USA: Kendal/Hunt Publishing Company.
Moses, R. (2001). Radical equations: math literacy and civil rights. Boston: Beacon
press.
Norwood, K. S. (1994). The effect of instructional approach on mathematics anxiety
and achievement. School Science and Mathematics, 94, 248-254.
Resek, D. and Rupley, W. H. (1980). Combating Mathophobia with a conceptual
approach toward mathematics. Educational studies in Mathematics, 11, 423-441.
Richardson, F.C. & Suinn, R.M. (1972). The mathematics anxiety rating scale:
Psychometric data. Journal of Counceling Psychology, 19, 551-554.
Schoenfeld, A. H. (2002). Making mathematics work for all children: Issues of
Standards, Testing, and Equity. Educational researcher, 31, 13-25.
Skiba, A. E. (1990). Reviewing an old subject: math anxiety. Mathematics Teacher,
90, 188-189.
Spikell, M. (1993). Teaching mathematics with manipulatives: A resource of activities
for the K-12 teacher. New York: Allyn and Bacon.
Tobias, S. (2001). Overcoming Math Anxiety. New York: W.W. Norton & CO.
Voolich, E. (1993). Using biographies to humanize the mathematics class. Arithmetic
Teacher, 41, 16-19.
Wigfield, A. & Meece, J. L.(1988). Math anxiety in elementary and secondary school
students. Journal of Educational Psychology, 80, 210-216.
Zaslavsky, C. (1994). Fear of math: How to get over it and get on with jour life. New
Brunswick, N. J. :Rutgers University Press.