[ Home ] [ Up ]

ΕΧΕΙ ΚΑΠΟΙΑ ΑΞΙΑ ΤΟ ΜΑΘΗΜΑΤΙΚΟ ΛΟΓΙΣΜΙΚΟ ΓΙΑ ΤΗΝ ΚΑΤΑΣΚΕΥΗ ΜΙΑΣ ΑΠΟΔΕΙΞΗΣ;

Μπάμπης Τουμάσης

Νόρμαν 33,  262 23, Πάτρα

Τηλ: 2610-455003, 6939176095

Abstract

Proofs are a beautiful and integral part of mathematics and some believe that they consist the heart and the corner stone of mathematics. Although computers can be used to do mathematics and they have come to be accepted as valuable companions to teaching and learning, yet in one important domain - crafting proofs – their usefulness remains an open question. In this paper we present some examples where the technology has allowed us to pursue a proof path. The interactivity on display goes had in had with careful reasoning and finally there are some instances where the creativity involved in developing proofs is something with a computer can helps.

Περίληψη

Οι αποδείξεις συνιστούν ένα όμορφο και αναπόσπαστο μέρος των μαθηματικών. Μολονότι οι υπολογιστές μπορεί να χρησιμοποιηθούν για να παράγουν μαθηματικά και έχουν γίνει αποδεκτοί ως πολύτιμα εργαλεία διδασκαλίας και μάθησης, η χρησιμότητά τους στην κατασκευή αποδείξεων παραμένει ένα ανοιχτό ζήτημα. Στην εργασία αυτή παρουσιάζουμε ορισμένα παραδείγματα στα οποία η τεχνολογία μας δίνει τη δυνατότητα να διαμορφώσουμε ένα αποδεικτικό μονοπάτι. Η διαδραστικότητα με την οθόνη του υπολογιστή προχωρά χέρι-χέρι με την προσεκτική σκέψη και τελικά βλέπουμε ότι  υπάρχουν κάποιες περιπτώσεις όπου ο υπολογιστής βοηθάει στη δημιουργική διαδικασία κατασκευής των αποδείξεων.

Εισαγωγή

     Είναι γεγονός πλέον ότι η διδασκαλία των μαθηματικών στην αρχή της τρίτης χιλιετίας μπαίνει σε μια νέα εποχή με την εμφάνιση του Η/Υ και του μαθηματικού λογισμικού το οποίο έχει αναπτυχθεί πρόσφατα (de Villiers, 1998). Η τεχνολογία αλλάζει δυναμικά τον τρόπο διδασκαλίας των μαθηματικών, όχι τόσο γιατί είναι παρούσα εδώ όσο γιατί είναι παρούσα παντού. Ιστορικά ως γνωστόν, ο ηλεκτρονικός υπολογιστής δημιουργήθηκε με βάση κυρίως τις ανάγκες που έθετε η πολεμική βιομηχανία για πολύπλοκους υπολογισμούς στη βαλλιστική και την κρυπτογραφία (Williams,1985). Ήταν μια φυσιολογική εξέλιξη στις επίμονες και συνεχείς προσπάθειες του ανθρώπου, εδώ και χιλιάδες χρόνια, να επινοεί και χρησιμοποιεί μηχανικά υπολογιστικά εργαλεία, όπως τον άβακα το 4000 περίπου π.χ., το μηχανισμό των Αντικυθήρων το 87 π.χ., τους ράβδους του Νάπιερ το 1610, τη μηχανή του Pascal το 1642 κ.λ.π. ( Τουμάσης & Αρβανίτης, 2003).

     Από τα μέσα της δεκαετίας του 1980 και μετά, αρχίζει πλέον η εντονότερη δραστηριοποίηση των εταιρειών λογισμικού, προκειμένου να υποστηρίξουν την εφεύρεση που άλλαξε -  και εξακολουθεί να αλλάζει – πολλά δεδομένα της καθημερινής ζωής. Σήμερα ο κάτοχος ενός απλού PC έχει δυνατότητες ήχου και γραφικών που κόβουν την ανάσα. Έτσι, εκτός από τις βασικές και κλασικές εφαρμογές επεξεργασίας κειμένου, λογιστικών φύλλων, βάσεων δεδομένων κ.λ.π., μπορεί να κάνει και εκατοντάδες άλλα πράγματα. Οι δυνατότητες που προσφέρουν αυτά τα λογισμικά μετατρέπουν σιγά- σιγά τον ηλεκτρονικό υπολογιστή σε ένα ισχυρό επιστημονικό αλλά και παιδαγωγικό εργαλείο.

     Στην περιοχή των μαθηματικών έχουν αναπτυχθεί αξιόλογα λογισμικά, τα οποία μπορούν να ταξινομηθούν σε δυο μεγάλες κατηγορίες. Στην πρώτη κατηγορία ανήκουν αυτά που έχουν σχεδιαστεί ειδικά για εκπαιδευτικούς σκοπούς, όπως π.χ. Cabri, Sketchpad, Sinderella, Function Probe, και άλλα. Στη δεύτερη, περιλαμβάνονται αυτά που έχουν τη δυνατότητα να εκτελούν και συμβολικούς υπολογισμούς, τα λεγόμενα συμβολικά συστήματα ή πακέτα (Computer Algebra Systems ή CAS) και είναι κατάλληλα, τόσο για ερευνητικούς σκοπούς όσο και για εκπαιδευτική χρήση, όπως το Mathematica, Derive, Maple, Mathcad και άλλα (Peschek, 1998 ^. Leinba et all, 2002).

     Tα παραπάνω λογισμικά, μολονότι είναι ιδανικά για πειραματισμό, εξερεύνηση, επεξεργασία δεδομένων και εκτέλεση υπολογισμών, εντούτοις δεν έχουν τη δυνατότητα να κατασκευάσουν μια απόδειξη, αφού η η τελευταία απαιτεί την ανθρώπινη επινοητικότητα, την οποία προς το παρόν τουλάχιστον, η υπάρχουσα τεχνολογία δεν είναι σε θέση να ενσωματώσει σε ένα λογισμικό πακέτο (Hoyles & Jones, 1998). Έτσι έχει εδραιωθεί η άποψη ότι η απόδειξη στα μαθηματικά, η οποία αποτελεί εξάλλου την καρδιά και το θεμέλιο λίθο της μαθηματικής επιστήμης, είναι το αναμφισβήτητο προνόμιο του ανθρώπινου εγκεφάλου, ο οποίος αποτελεί και θα αποτελεί ίσως για μεγάλο χρονικό διάστημα ακόμη, τον ιδανικό υπολογιστή (Hana & Jahnke, 1996^. Scher, 1999).

     Είναι αλήθεια ότι τα εξελιγμένα μαθηματικά λογισμικά προσφέρουν σε ορισμένες περιπτώσεις μια ισχυρή οπτική μαρτυρία για την αλήθεια ή όχι μιας πρότασης. Ειδικά το δυναμικό γεωμετρικό λογισμικό δίνει τη δυνατότητα να ελεγχθεί οπτικά η αλήθεια μιας γεωμετρικής πρότασης – εικασίας μέσα από τη συνεχή μεταβολή της μορφής ενός σχήματος έτσι ώστε να διατηρούνται τα συγκεκριμένα χαρακτηριστικά της κατασκευής ( Τουμάσης & Αρβανίτης, 2003)

     Βεβαίως, η δυνατότητα αλληλεπίδρασης με το γεωμετρικό σχηματισμό μπορεί να ικανοποιεί τους μαθητές και να πείθει για την ύπαρξη μιας ιδιότητας, π.χ. για το ότι τα τρία ύψη ενός τριγώνου συναντώνται σε ένα σημείο, σε καμιά περίπτωση όμως δεν συνιστά μια απόδειξη. Η διαδραστικότητα δεν εξηγεί για πιο λόγο συμβαίνει κάτι τέτοιο ( Mariotti, 2000).

     Το ερώτημα λοιπόν που εγείρεται είναι τούτο: Θα πρέπει ο ρόλος των μαθηματικών λογισμικών πακέτων να περιορίζεται στις προκαταρκτικές μόνο φάσεις της μαθηματικής δημιουργίας, δηλαδή, την επεξεργασία και αποθήκευση δεδομένων, την εξερεύνηση, τον πειραματισμό και τη διαμόρφωση εικασιών; Στην εργασία αυτή θα προσπαθήσουμε να αναθεωρήσουμε την κυρίαρχη αυτή αντίληψη όσον αφορά τη σχέση της τεχνολογίας με την απόδειξη στα μαθηματικά και να δείξουμε ότι σε ορισμένες περιπτώσεις η τεχνολογία μπορεί να παίξει έναν δραστήριο και ενεργητικό ρόλο στη διαμόρφωση της συλλογιστικής διαδικασίας που οδηγεί στην κατασκευή μιας απόδειξης.

     Παρακάτω θα παρουσιάσουμε τρία σχετικά παραδείγματα – προβλήματα όπου η χρήση των κατάλληλων λογισμικών με τις δυνατότητες που προσφέρουν μπορεί να διευκολύνει την αλυσίδα της παραγωγικής σκέψης και να βοηθήσει στην κατασκευή μιας απόδειξης. Τα δύο προβλήματα είναι από τη γεωμετρία και το άλλο από την Άλγεβρα – Ανάλυση.

Χρήση του δυναμικού γεωμετρικού λογισμικού.

Πρόβλημα 1: Δίνεται κύκλος (Ο, R), μια διάμετρος  ΑΒ και ένα σημείο του

                       Γ διαφορετικό των Α και Β. Θεωρούμε τις εφαπτόμενες του

                       κύκλου στα σημεία Β και Γ, αντιστοίχως, οι οποίες τέμνονται

                       στο σημείο P. Η κάθετος από το Γ προς τη διάμετρο ΑΒ την

                       τέμνει στο Δ, ενώ η ευθεία ΑΠ τέμνει την ευθεία ΓΔ στο Ε.

                       να υπολογίσετε το λόγο .

( Το παραπάνω πρόβλημα τέθηκε ως θέμα στον 61^ο πανελλήνιο μαθηματικό διαγωνισμό «ο Ευκλείδης» της ΕΜΕ, το 2001).

• Με τη βοήθεια των γεωμετρικών εργαλείων του Sketchpad, κατασκευάζουμε το σχήμα 1 από τα δεδομένα του προβλήματος. Από το μενού Μέτρηση μετράμε τα μήκη των τμημάτων ΓΕ και ΓΔ και με την εντολή Υπολογισμός υπολογίζουμε τον λόγο .

• Σύρουμε με το ποντίκι το σημείο Γ πάνω στον κύκλο και παρατηρούμε πώς αλλάζουν οι μετρήσεις.

Σχήμα 1

• Από το μενού Μέτρηση, επιλέγοντας πινακοποίηση και προσθήκη τιμών στον πίνακα, δημιουργείται ο πίνακας του σχήματος 1, που περιέχει τις τιμές των μετρήσεων για διαφορετικές θέσεις του σημείου Γ.

• Παρατηρούμε ότι ο λόγος  παραμένει πάντα σταθερός και ίσος με . Αυτό μας οδηγεί στο συμπέρασμα να διατυπώσουμε την εικασία ότι ΓΕ = ΓΔ και .

• Σύροντας το σημείο Γ παρατηρούμε ότι PΓ = PΒ, πράγμα που εξηγείται γιατί είναι εφαπτόμενα τμήματα στον κύκλο. Δεν φαίνεται όμως να υπάρχει κάποια άλλη σχέση μεταξύ ευθυγράμμων τμημάτων ή γωνιών η οποία θα μας οδηγούσε στη λύση του παζλ. Αποφασίζουμε λοιπόν να φέρουμε βοηθητικές ευθείες και γι’ αυτό ενώνουμε το Γ με τα Α και Β και προεκτείνουμε την ΑΓ, η οποία τέμνει την προέκταση της ΒP στο Η. Σύροντας το Γ παρατηρούμε ότι ΗP = PΒ. Ίσως και αυτό να είναι το κλειδί της λύσης. Εδώ όμως φαίνεται ότι σταματά και η προσφορά του υπολογιστή. Δεν είναι σε θέση να βοηθήσει παραπέρα.
  
   

• Επικεντρώνουμε τις προσπάθειές μας στο να αποδείξουμε ότι το P είναι το μέσο του ΗΒ. Πράγματι, το τρίγωνο  είναι ορθογώνιο. Επίσης, ως συμπληρωματικές των ίσων γωνιών  και . Άρα ΗP = ΓP = PΒ και το P μέσο της ΗΒ. Στη συνέχεια θα πορευτούμε με ισότητα λόγων από τα όμοια τρίγωνα ΑΕΔ, ΑΒP και ΑΓΕ, ΑPΗ στηριζόμενοι στις προηγούμενες παρατηρήσεις μας. Πράγματι, , οπότε, ΔΕ = ΓΕ. Άρα  και η απόδειξη ολοκληρώθηκε.

Πρόβλημα 2: Θεωρούμε ευθύγραμμο τμήμα ΑΓ και σημείο Β στο

                       εσωτερικό του. Κατασκευάζουμε ισόπλευρα τρίγωνα ΑΒΔ

                       και ΒΓΕ προς το ίδιο μέρος του ευθυγράμμου τμήματος ΑΓ.

                       Αν οι ΑΕ και ΓΔ τέμνονται στο Ζ, να βρείτε τη γωνία ΑΖΔ.

(Το πρόβλημα αυτό τέθηκε ως θέμα στον 62^ο πανελλήνιο διαγωνισμό της Ε.Μ.Ε. «ο Θαλής» το 2001).

• Με τη βοήθεια των γεωμετρικών εργαλείων του Sketchpad κατασκευάζουμε το σχήμα 2 από τα δεδομένα του προβλήματος.
   

                                                                Σχήμα 2

• Από το μενού Μέτρηση μετράμε τη γωνία ΑΖΔ και βρίσκουμε ότι .
  
   

• Σύρουμε το σημείο Β πάνω στο τμήμα ΑΓ και παρατηρούμε ότι σε κάθε νέο σχηματισμό το μέτρο της γωνίας ΑΖΔ παραμένει σταθερό και ίσο με .
  
   

• Ανακαλύψαμε λοιπόν ότι το μέτρο της γωνίας ΑΖΔ είναι . Δεν χωράει αμφιβολία περί αυτού. Δεν μπορούμε όμως να σταματήσουμε εδώ γιατί το λογισμικό μας προσφέρει μόνο την οπτική – υπολογιστική βεβαιότητα, δεν μπορεί να εξηγήσει πώς προκύπτει αυτό το αποτέλεσμα. και πως συνδέεται με άλλες γνωστές προτάσεις. Μήπως μπορεί όμως να βοηθήσει στο να ανακαλυφθεί ένας δρόμος που οδηγεί στη διασύνδεση αυτού του αποτελέσματος με ήδη γνωστά αποτελέσματα; Μήπως μπορεί, δηλαδή, να βοηθήσει στην κατασκευή μιας απόδειξης; Από δω και πέρα αναμειγνύεται η ανθρώπινη ευφυΐα με τις δυνατότητες του λογισμικού στην προσπάθειά μας να ανακαλύψουμε στοιχεία ισότητας στο σχήμα.
  
   

• Σύροντας το σημείο Β πάνω στη ΒΓ παρατηρούμε ότι τα τρίγωνα ΑΒΕ και ΒΓΔ φαίνεται να παραμένουν ίσα για κάθε θέση του Β. Προσπαθούμε λοιπόν να αποδείξουμε ότι είναι πράγματι ίσα. Παρατηρούμε ότι ΑΒ = ΒΔ, ΒΕ = ΒΓ και  Από την ισότητα αυτή προκύπτει ότι , οπότε αφού (ως κατακορυφήν), τα τρίγωνα ΑHΒ και ΔHΖ θα έχουν και = . Δηλαδή, .
  
   

• Βλέπουμε, λοιπόν ότι ναι μεν το Sketchpad δεν είναι σε θέση να αποδείξει ότι η γωνία , έχει όμως δυνατότητες που αν τις αξιοποιήσουμε μας βοηθούν να συνθέσουμε μια απόδειξη.

Χρήση του Αλγεβρικού λογισμικού.

Πρόβλημα 3: Να αποδείξετε ότι το πολυώνυμο 3x⁴ – x² –2x +4 δεν έχει

                       πραγματικές ρίζες.

(Το πρόβλημα αυτό τέθηκε ως «άσκηση του μήνα» από την Ε.Μ.Ε. για το χρονικό διάστημα Δεκεμβρίου – Ιανουαρίου 2003/04, www.hms.gr/gr/sources/index_exercise.html).

• Με τη βοήθεια του Function Probe σχηματίζουμε τη γραφική παράσταση της συνάρτησης f με τύπο f(x) = 3x⁴ – x² –2x +4 και βλέπουμε (σχήμα 3) ότι πράγματι ισχύει f(x) > 0 για κάθε .

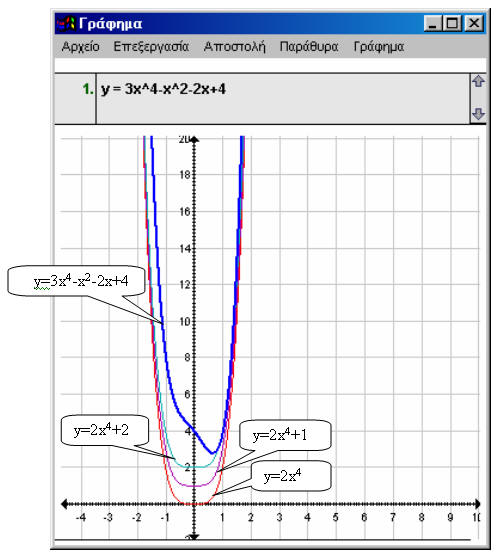
 Σχήμα 3

• Δοκιμάζουμε κάποιες συναρτήσεις με απλούστερο τύπο, οι οποίες να βρίσκονται «από κάτω» της f και πάνω από τον άξονα των χ, όπως για παράδειγμα, y = x⁴, y = 2x⁴, y = 3x⁴, y = 4x⁴ κ.λ.π. Σχηματίζουμε τη γραφική παράσταση της y = 2x⁴ και με τη βοήθεια του μενού Μεταφορά, την μετακινούμε κατακόρυφα ενώ ταυτόχρονα ο τύπος της εμφανίζεται στο πλαίσιο τύπων.

• Παρατηρώ οπτικά ότι για τη συνάρτηση g με τύπο g(x) = 2x⁴ + 2 ισχύει f(x)για κάθε x με το «=» για x = 1.
  
   

• Προσπαθούμε λοιπόν να αποδείξουμε με αλγεβρικό τρόπο ότι πράγματι f(x)  ή f(x) – g(x) ή x⁴ – x² – 2x +2  (1).
  
   

• Με παραγοντοποίηση, η οποία εάν είναι πολύπλοκη μπορεί να γίνει με το Derive, καταλήγουμε ότι (1) που ισχύει γιατί η διακρίνουσα του τριωνύμου είναι αρνητική. Άρα, 3x⁴ – x² –2x +4 2x⁴ +2 > 0 και επομένως το πολυώνυμο 3x⁴ – x² –2x +4 δεν έχει πραγματικές ρίζες.

Τελικές σκέψεις

     Οι αποδεικτικές μέθοδοι που περιγράψαμε παραπάνω βασίστηκαν στην αλληλεπίδραση του υπολογιστή με το ανθρώπινο μυαλό. Η αλληλεπίδραση αυτή του μυαλού με εκείνο που εμφανίζεται πάνω στην οθόνη του υπολογιστή αναμφίβολα δεν αποτελεί υποκατάστατο της απόδειξης. Συνιστά όμως ένα ιδιότυπο μείγμα τεχνολογίας και προσεκτικής σκέψης, η οποία χαράζει ένα μονοπάτι που οδηγεί τελικά στην κατασκευή μιας απόδειξης.

     Βεβαίως, δεν ισχυρίζεται κανείς ότι όλα τα προβλήματα μπορεί να ωφεληθούν απ’ αυτή τη ιδιότυπη μείξη. Υπάρχουν περιπτώσεις που το ανθρώπινο μυαλό πρέπει να προχωρήσει μόνο του με μόνο βοηθό τη διορατικότητα , τη διαίσθηση και την εμπειρία, ανοίγοντας μονοπάτια από το τίποτα. Έχουμε όμως την πεποίθηση, αναλογιζόμενοι και τους τρομακτικούς ρυθμούς εξέλιξης και ανάπτυξης της υπολογιστικής τεχνολογίας, ότι ο υπολογιστής θα υπεισέρχεται ολοένα και σε περισσότερες μαθηματικές περιοχές και θα προσφέρει τις δυνατότητές του με ικανοποιητικά αποτελέσματα στην παραπέρα εξερεύνηση και ανάπτυξή τους.

     Με αυτήν την έννοια, η διδασκαλία των μαθηματικών σ’ ένα υπολογιστικό περιβάλλον δεν θα πρέπει να περιορίζεται μόνο στην αξιοποίηση του υπολογιστή ως εργαλείου αισθητοποίησης των εννοιών, εκτέλεσης υπολογισμών ή πειραμάτων για τη δημιουργία υποθέσεων και εικασιών, αλλά θα πρέπει εκεί όπου είναι δυνατόν, να επεκτείνεται και παραπέρα στην εξερεύνηση αποδεικτικών μονοπατιών και διαμόρφωση συλλογισμών.

     Ο δάσκαλος των μαθηματικών θα πρέπει να υποδεικνύει στους μαθητές τρόπους αξιοποίησης των κατάλληλων λογισμικών, έτσι ώστε μέσα από τη συνεχή αλληλεπίδραση και διαδραστικότητα ανθρώπου – υπολογιστή να αναδεικνύεται ο ενεργητικός ρόλος που μπορεί να παίξει ο τελευταίος στη συλλογιστική διαδικασία.

ΑΝΑΦΟΡΕΣ

De Villiers, M. (1998) : An alternative approach to proof in dynamic ge

        ometry : some personal reflections. In King and Schattschneider (Eds).

        Geometry Turned On: Dynamic Software in Learning, Teaching and

        Research. Washington,D.C.: The Mathematical Association of Ame-

        rica, 15-24.

Hanna, G and Jahnke, N. (1996): Proof and Proving. In A. J. Bishop(Ed.),

        International handbook on Mathematics Education, Dordrecht: Kluwer

.

Hoyles, C. and Jones, K (1998): Proof in Dynamic Geometry Contexts. In

        C.Mammana and V. Villani (Eds), Perspectives on the Teaching of Ge-

        ometry for the 21^st Century, Dordrecht: kluwer.

Leinba, C., Poutney, J. (2002): Appropriate use of CAS in the teaching and

         learning of mathematics. Int. J. Math. Educ. Sci. Technology, 33(1), 8-

        14.

Mariott, M. A. (2000): Introduction to Proof: The Mediation of a Dynamic

         software Environment. Educational Studies in Mathematics, 44(1/2),

        151-161.

Peschek,W. (1998): Mathematical Concepts and New Technology. In: Pro

        ceedings of the International Conference on the Teaching of Mathema-

        tics, John Wiley & Sons, new York, 242-245.

Scher, D. (1999): Problem Solving and Proof in the age of dynamic geome-

        try. Micromath, 15(1), 24-30.

Τουμάσης, Μπ., Αρβανίτης,Τ. (2003): Διδασκαλία μαθηματικών με χρήση

        Η/Υ. Εκ. Σαββάλας, Αθήνα.

Williams, M.: (1985): A history of computing technology. Prentice-Hall,

        Englewood Cliffs, N. Jersey.