2.1- Οι πράξεις και οι ιδιότητές τους- Εισαγωγή

Οι πράξεις και οι ιδιότητές τους - Εισαγωγή
Οι πράξεις και οι ιδιότητές τους - Εισαγωγή

Α. Θεωρία
Πακέτο θεωρίας

B. Ασκήσεις
Πακέτα λυμένων ασκήσεων , για εμπέδωση της θεωρίας 1. Ασκήσεις ανάπτυξης 2 . Ασκήσεις Σωστό- Λάθος 3 . Ασκήσεις πολλαπλής επιλογής 4 . Ασκήσεις Αντιστοίχισης 5 . Ασκήσεις Διάταξης 6 . Ασκήσεις συμπλήρωσης κενού

Γ. Eφαρμογές

Δημιουργία τριγωνικών αριθμών Οι αρχαίοι Έλληνες κατέταξαν τους φυσικούς σε κατηγορίες , όπως λ.χ τρίγωνους , τετράγωνους , πεντάγωνους κ.λ.π Με την εφαρμογή αυτή , δείτε τι είναι οι τρίγωνοι αριθμοί , και με την βοήθεια της γεννήτριας παραγωγής τρίγωνων αριθμών , δείτε τους 168 πρώτους τρίγωνους αριθμούς

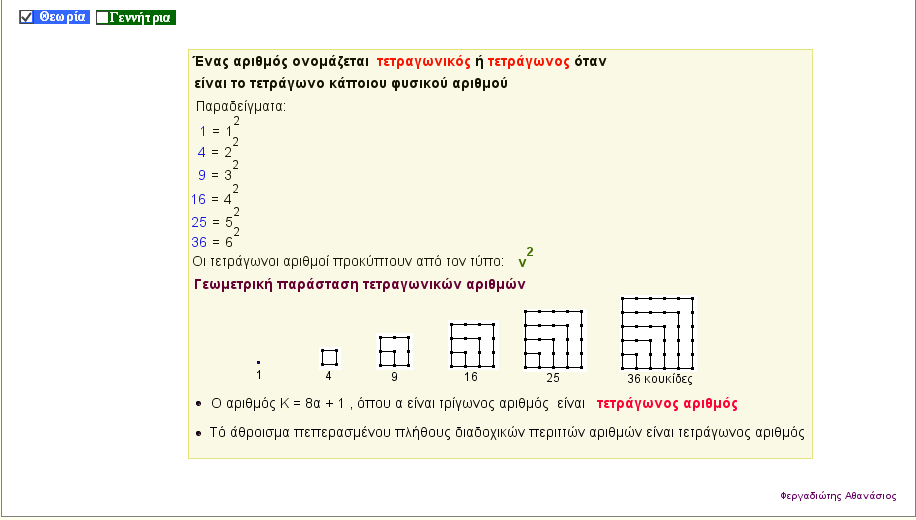
Δημιουργία τετραγωνικών αριθμών Οι αρχαίοι Έλληνες κατέταξαν τους φυσικούς σε κατηγορίες , όπως λ.χ τρίγωνους , τετράγωνους , πεντάγωνους κ.λ.π Με την εφαρμογή αυτή , δείτε τι είναι οι τετράγωνοι αριθμοί , και με την βοήθεια της γεννήτριας παραγωγής τετράγωνων αριθμών , δείτε τους 189 πρώτους τετράγωνους αριθμούς
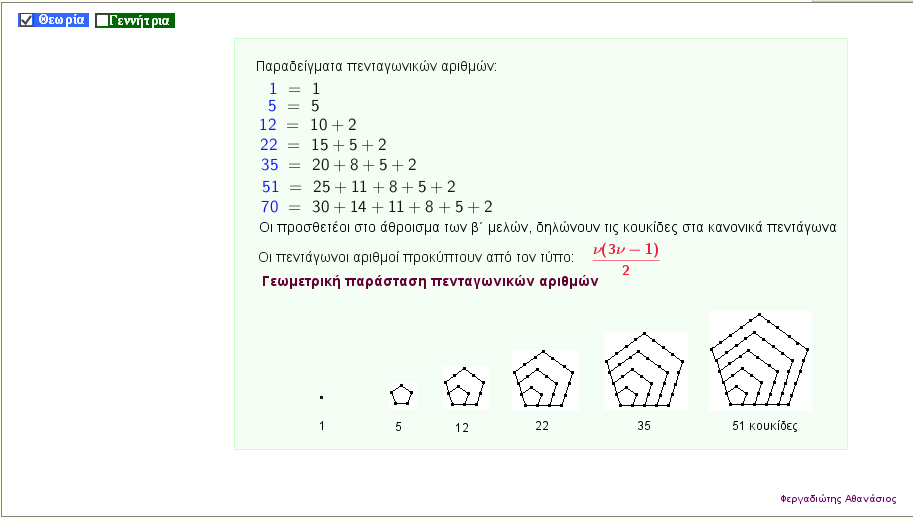
Δημιουργία πενταγωνικών αριθμών Οι αρχαίοι Έλληνες κατέταξαν τους φυσικούς σε κατηγορίες , όπως λ.χ τρίγωνους , τετράγωνους , πεντάγωνους κ.λ.π Με την εφαρμογή αυτή , δείτε τι είναι οι πεντάγωνοι αριθμοί , και με την βοήθεια της γεννήτριας παραγωγής πεντάγωνων αριθμών , δείτε τους 189 πρώτους πεντάγωνους αριθμούς

Δημιουργία πολυγωνικών αριθμών Με την εφαρμογή αυτή , δείτε τους πολύγωνους αριθμούς που θέλετε, βάζοντας την τιμή του x . Για x = 3 , παίρνετε τους τριγωνικούς αριθμούς ,για x = 12 , παίρνετε τους δωδεκαγωνικούς αριθμούς , και με την βοήθεια της γεννήτριας παραγωγής πολύγωνων αριθμών , δείτε τους 189 πρώτους πολύγωνους αριθμούς

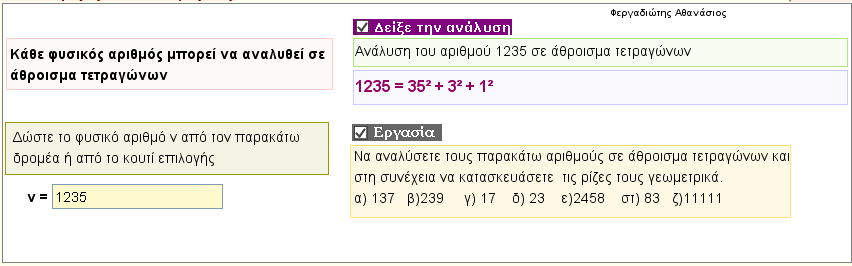
Ανάλυση φυσικού αριθμού σε άθροισμα τετραγώνων Κάθε φυσικός αριθμός αναλύεται σε άθροισμα τετραγώνων. Δώστε ένα φυσικό αριθμό ν ,και δείτε την ανάλυσή του σε άθροισμα τετραγώνων άλλων φυσικών αριθμών.

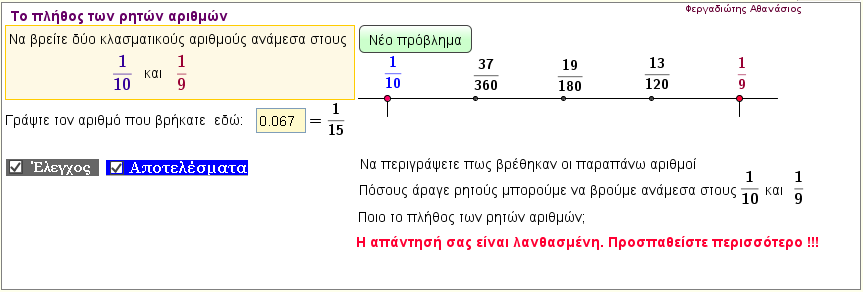
Το πλήθος των ρητών αριθμών Πόσοινάραγε ρητοί αριθμοί υπάρχουν μεταξύ δύο άλλων ρητών ; Υπάρχουν άλλοι ρητοί μεταξύ των $\frac{1}{231}$ και $\frac{1}{232}$ ; Αν υπάρχουν , πόσοι είναι; Γενικά , πόσοι ρητοί υπάρχουν μεταξύ δύο αριθμών α και β που βρίσκονται ''πολύ κοντά'' ο ένας στον άλλο;

Γεωμετρική κατασκευή άρρητων αριθμών Δώστε ένα φυσικό αριθμό ν ,και δείτε την ανάλυσή του σε άθροισμα τετραγώνων φυσικών αριθμών. Στη συνέχεια κατασκευάστε τον αριθμό αυτό , γεωμετρικά Αν π.χ δώσετε ν = 137 θα κατασκευαστεί η $ \sqrt{137} $

Γεωμετρική κατασκευή άρρητων αριθμών - Εργασία για τον μαθητή Διαβάστε προσεκτικά τις οδηγίες που δίνονται στην εφαρμογή. Στη συνέχεια, με τη χρήση του προγράμματος Geogebra, κατασκευάστε τους αριθμούς που σας δίνονται , γεωμετρικά Μπορείτε να κατασκευάσετε τους αριθμούς $ \sqrt{47} $ , $ \sqrt{59} $ ;

"Τυποποιημένη μορφή" αριθμού - Τεστ Kάθε αριθμός πού έχει την μορφή α.10^ν με 0 < \|α\| < 10 και ν ακέραιος , λέμε ότι είναι γραμμένος στην "τυποποιημένη μορφή". Δώστε έναν οποιονδήποτε αριθμό και βρείτε στη συνέχεια την τυποποιημένη του μορφή (Η εφαρμογή αποτελεί τεστ)

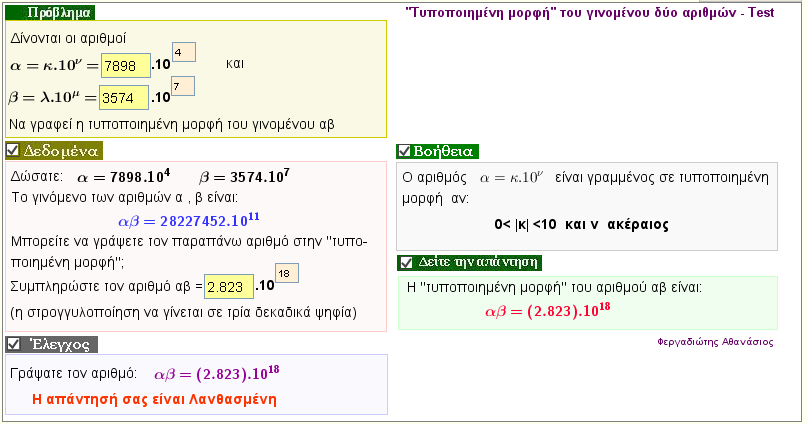
"Τυποποιημένη μορφή" του γινομένου δύο αριθμών - Τεστ Kάθε αριθμός πού έχει την μορφή α.10^ν με 0 < \|α\| < 10 και ν ακέραιος , λέμε ότι είναι γραμμένος στην "τυποποιημένη μορφή". Δώστε δύο οποιουσήποτε αριθμούς α και β και βρείτε στη συνέχεια την τυποποιημένη του μορφή του γινομένου τους (Η εφαρμογή αποτελεί τεστ)

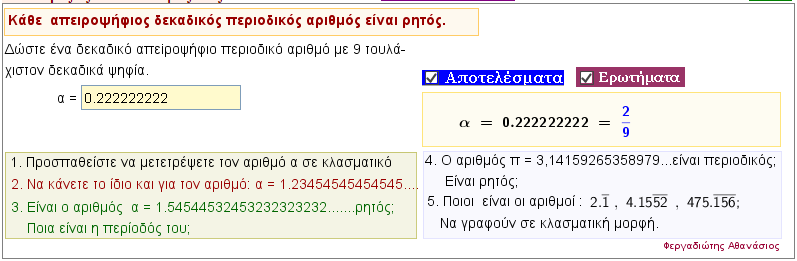
Μετατροπή απειροψήφιου δεκαδικού περιοδικού σε κλασματικό Δώστε ένα δεκαδικό απειροψήφιο περιοδικό αριθμό α ,και δείτε σε ποιο κλασματικό αριθμό αντιπροσωπεύεται.

Υπολογισμός παραστάσεων - Τεστ Δώστε μία παράσταση του x , και εν συνεχεία υπολογίστε την και γράψτε το αποτέλεσμά σας στο κάτω μέρος της εφαρμογής. Ελέγξτε , αν το αποτέλεσμα πού βρήκατε έναι σωστό ή λανθασμένο. (Η εφαρμογή αποτελεί τεστ)