4.1 - Ανισώσεις 1ου βαθμού



Ανισώσεις 1ου βαθμού

Α. ΑΣΚΗΣΕΙΣ			B. Θεωρία σχολικού βιβλίου
1 . Ασκήσεις ανάπτυξης 2 . Ασκήσεις συμπλήρωσης κενού

Γ. Τεστ
Ένα τεστ 14 ερωτήσεων . Κάντε κλικ εδώ

Δ. ΕΦΑΡΜΟΓΕΣ


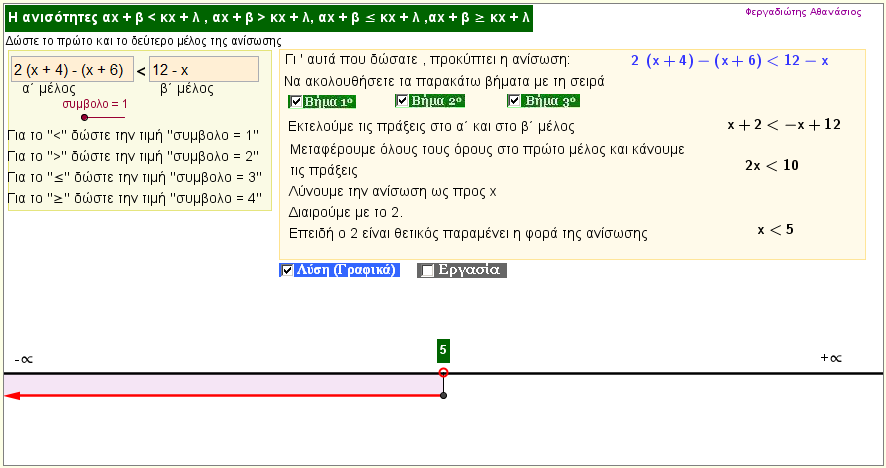
Η ανίσωση αx + β > κx + λ Δώστε τα δύο μέλη μιας ανίσωσης ως παραστάσεις του αγνώστου x , και δείτε πως την λύνουμε βήμα προς βήμα Στη συνέχεια , δείτε και την λύση της , αν υπάρχει , στο άξονα x΄x.

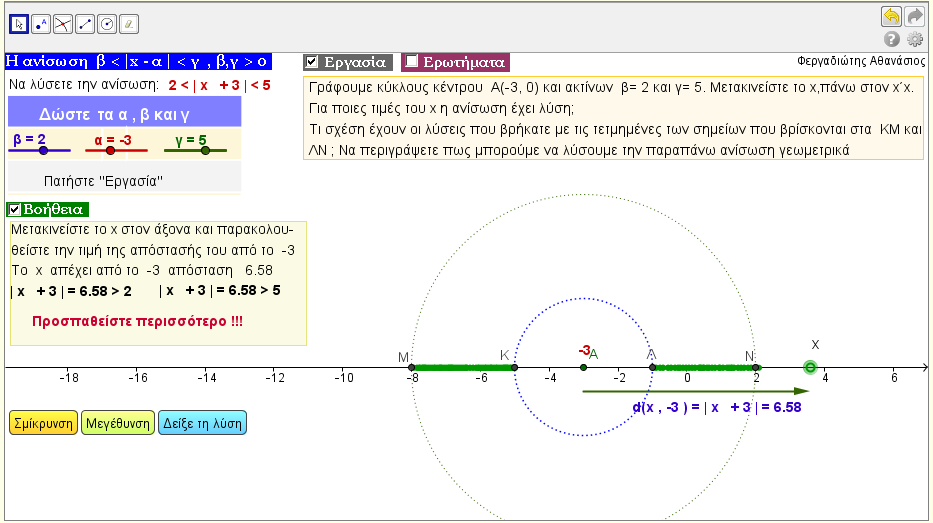
Η ανίσωση α < \|x - k\| < β Δώστε τα α , β , k της ανίσωσης. Η λύση της ανίσωσης γίνεται με γεωμετρικό τρόπο , με την βοήθεια ομόκεντρων κύκλων.

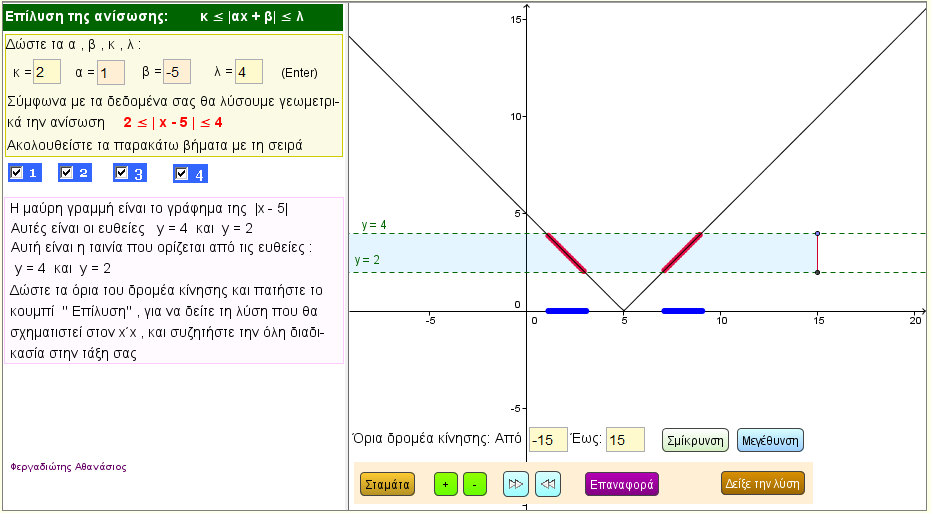
Η ανίσωση α < \|κx + λ\| < β Δώστε τα α , β , κ , λ της ανίσωσης. Η λύση της ανίσωσης γίνεται με γεωμετρικό τρόπο , με την βοήθεια του γραφήματος της συνάρτησης f(x) = \|κx + λ\| και της ταινίας (ζώνης) που ορίζεται από τις ευθείες με εξισώσεις y = α και y = β.

Λύση ανίσωσης της μορφής \|αx + β\| < γ Λύστε την ανίσωση \|αx + β\| < γ , για τις διάφορες τιμές των παραμέτρων α , β , γ. Δείτε πότε η παραπάνω ανίσωση έχει λύση , πότε είναι αδύνατη στο R , και , πότε ισχύει για όλους τους πραγματικούς αριθμούς

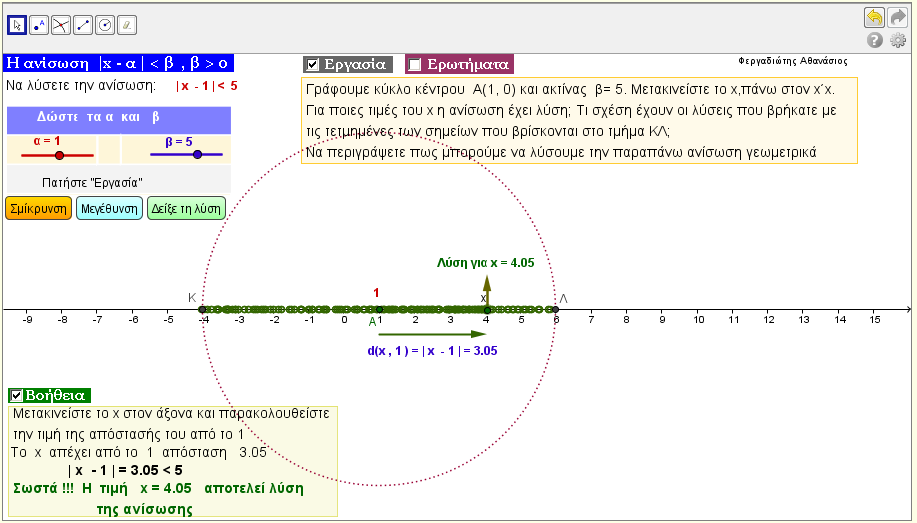
Λύση ανίσωσης της μορφής \|x - α\| <β Λύστε την ανίσωση \|αx + β\| < γ , για τις διάφορες τιμές των παραμέτρων α , β , γ. Δείτε πότε η παραπάνω ανίσωση έχει λύση , πότε είναι αδύνατη στο R , και , πότε ισχύει για όλους τους πραγματικούς αριθμούς. Για την επίλυση της παραπάνω άνίσωσης χρησιμοποιείται κύκλος με γνωστό κέντρο και σταθερή γνωστή ακτίνα.

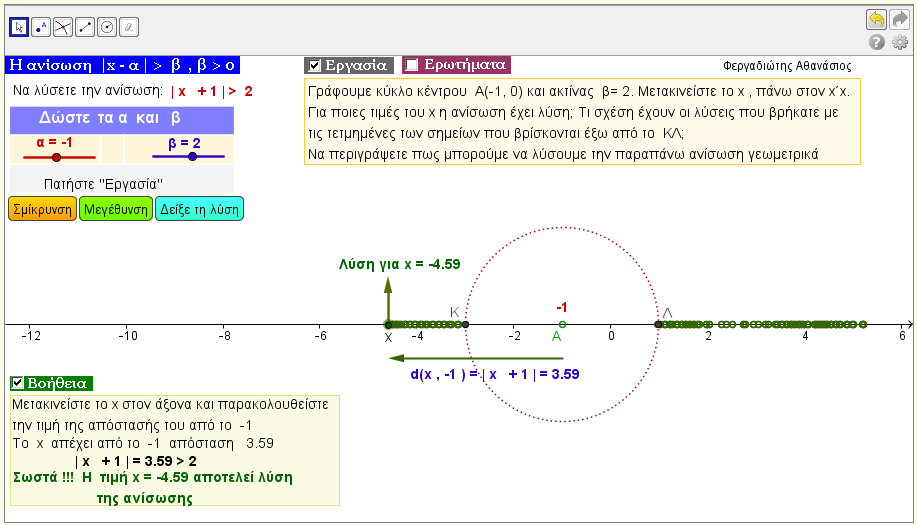
Λύση ανίσωσης της μορφής \|x - α\| > β Λύστε την ανίσωση \|αx + β\| > γ , για τις διάφορες τιμές των παραμέτρων α , β , γ. Δείτε πότε η παραπάνω ανίσωση έχει λύση , πότε είναι αδύνατη στο R , και , πότε ισχύει για όλους τους πραγματικούς αριθμούς. Για την επίλυση της παραπάνω άνίσωσης χρησιμοποιείται κύκλος με γνωστό κέντρο και σταθερή γνωστή ακτίνα.

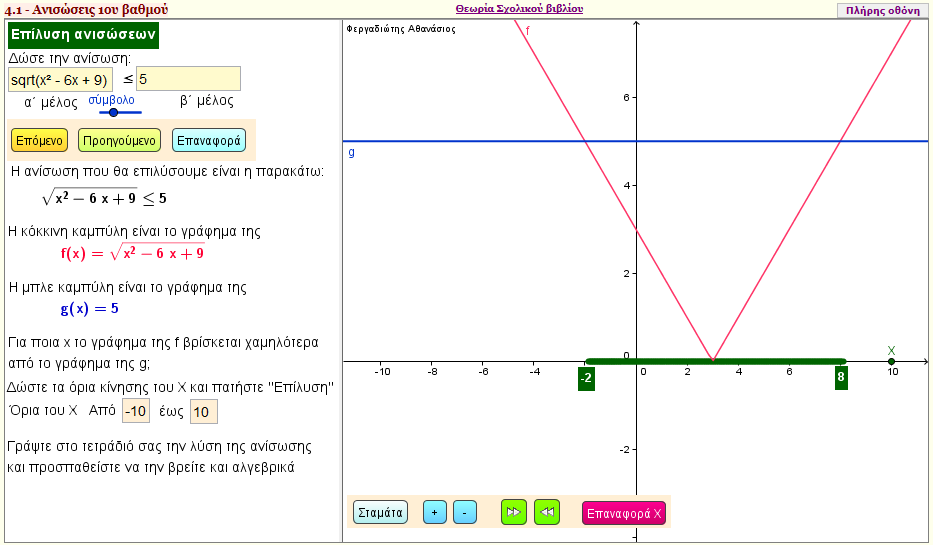
Άσκηση 9 Α΄ Ομάδας Να λύσετε την ανίσωση 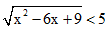Mε τη βοήθεια της εφαρμογής αυτής να λύσετε τις ασκήσεις: 1. Άσκηση 1 Α΄ Ομάδας 2. Άσκηση 5 Α΄ Ομάδας 3. Άσκηση 6 Α΄ Ομάδας 4. Άσκηση 8 Α΄ Ομάδας

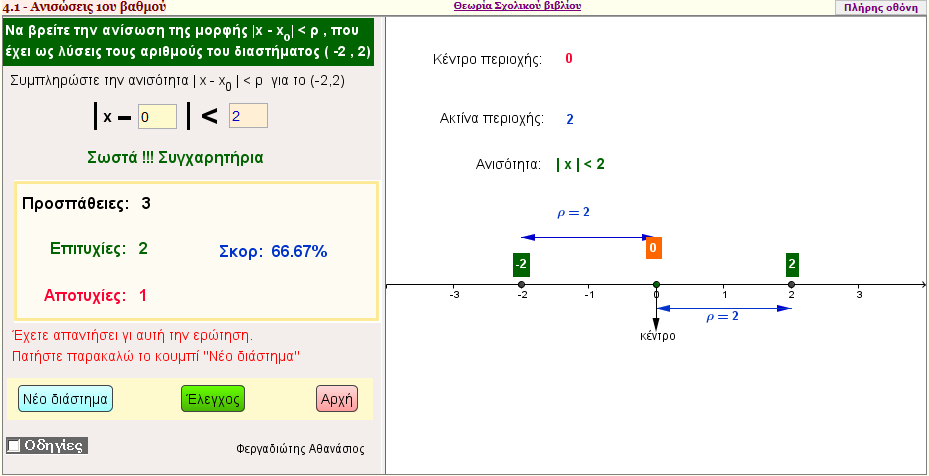
Άσκηση 10 Α΄ Ομάδας Να βρείτε την ανίσωση της μορφής \|x - x₀\| < ρ , που έχει ως λύσεις , τους αριθμούς του διαστήματος (-7 , 3)

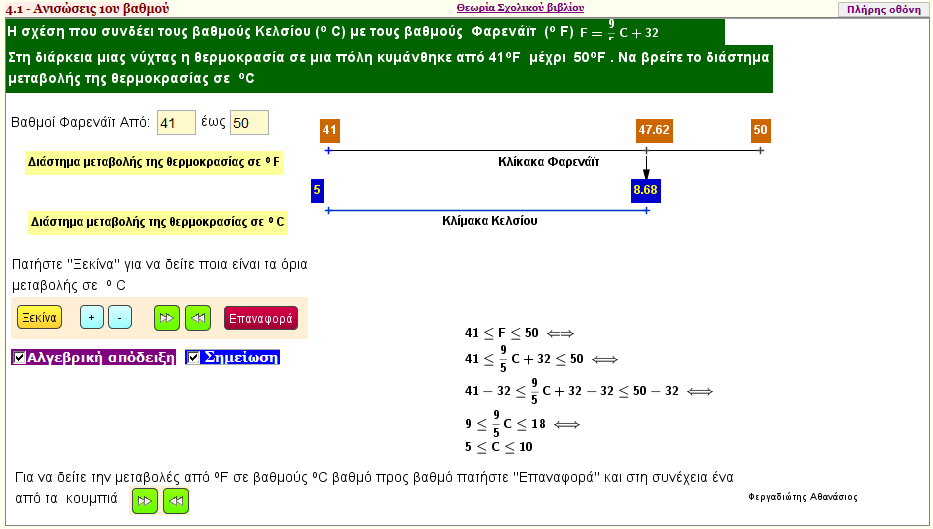
Άσκηση 11 Α΄ Ομάδας Η σχέση που συνδέει τους βαθμούς Κελσίου (^ο C) με τους βαθμούς Φαρενάϊτ (^ο F) είναι η F = 9/5C + 32 . Στη διάρκεια μιας νύχτας η θερμοκρασία σε μια πόλη κυμάνθηκε από 41^οF μέχρι 50^οF . Να βρείτε το διάστημα μεταβολής της θερμοκρασίας σε ^ο C.

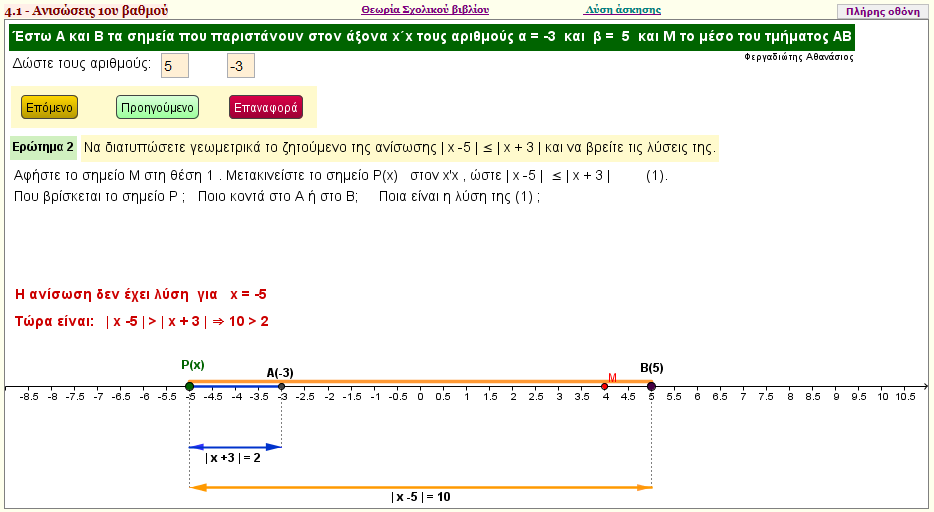
Άσκηση 3 Β΄ ομάδας Έστω Α και Β τα σημεία που παριστάνουν σε έναν άξονα τους αριθμούς -3 και 5 και Μ το μέσο του τμήματος ΑΒ. i) Ποιος αριθμός αντιστοιχεί στο σημείο Μ; ii) Να διατυπώσετε γεωμετρικά το ζητούμενο της ανίσωσης \|x - 5\| < \|x + 3\| και να βρείτε τις λύσεις της. iii) Να επιβεβαιώσετε αλγεβρικά τα συμπεράσματά σας.

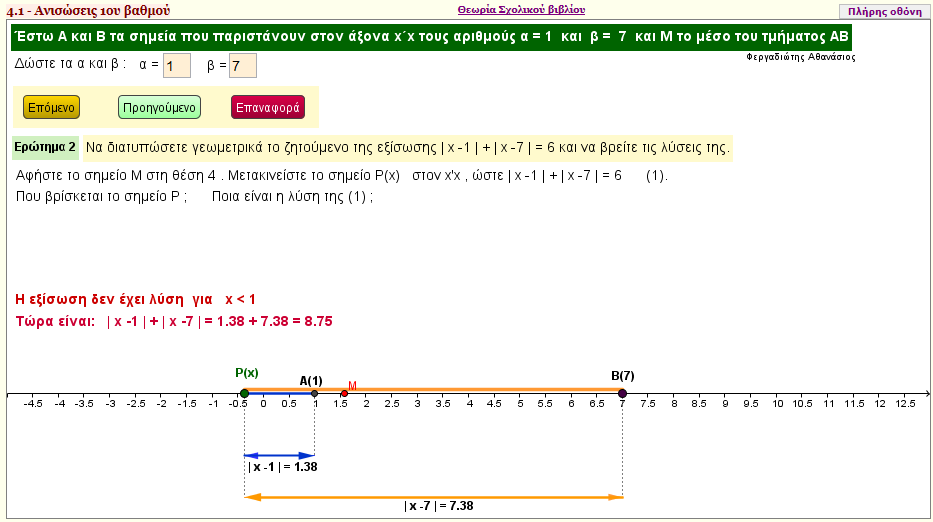
Άσκηση 4 Β΄ ομάδας Έστω Α και Β τα σημεία που παριστάνουν σε έναν άξονα τους αριθμούς 1 και 7 και Μ το μέσο του τμήματος ΑΒ. i) Ποιος αριθμός αντιστοιχεί στο σημείο Μ; ii) Να διατυπώσετε γεωμετρικά το ζητούμενο της εξίσωσης \|x - 1\| + \|x - 7\| = 6 και να βρείτε τις λύσεις της. iii) Να επιβεβαιώσετε αλγεβρικά τα συμπεράσματά σας, αφού προηγουμένως συντάξετε πίνακα προσήμου των παραστάσεων \|x - 1\| και \|x - 7\|.