| 1.5 Εσωτερικό γινόμενο διανυσμάτων |
|
|
|
| |
|
|
|
| Α. Θεωρία |
|
|
Β. Ασκήσεις |
| Πακέτο θεωρίας βιβλίου |
|
|
Ασκήσεις ανάπτυξης |
| Eσωτερικό γινόμενο διανυσμάτων |
|
|
Ασκήσεις αντιστοίχισης |
| |
|
|
Ασκήσεις πολλαπλής επιλογής |
| |
|
|
Ασκήσεις Σωστό - Λάθος |
| Kριτήριο αξιολόγησης |
|
|
Ασκήσεις διάταξης |
| Κριτήριο 1 |
|
|
Ασκήσεις συμπλήρωσης κενού |
| |
|
|
|
| |
|
|
Ασκήσεις σχολικού βιβλίου |
| |
|
|
Γενικές ασκήσεις κεφαλαίου |
| Β. VIDEO |
|
|
|
| Προβολή διανύσματος - Εφαρμογές |
|
|
|
| Άσκηση 3 |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| Γ. Εφαρμογές |
|
|
|
| |
|
|
|
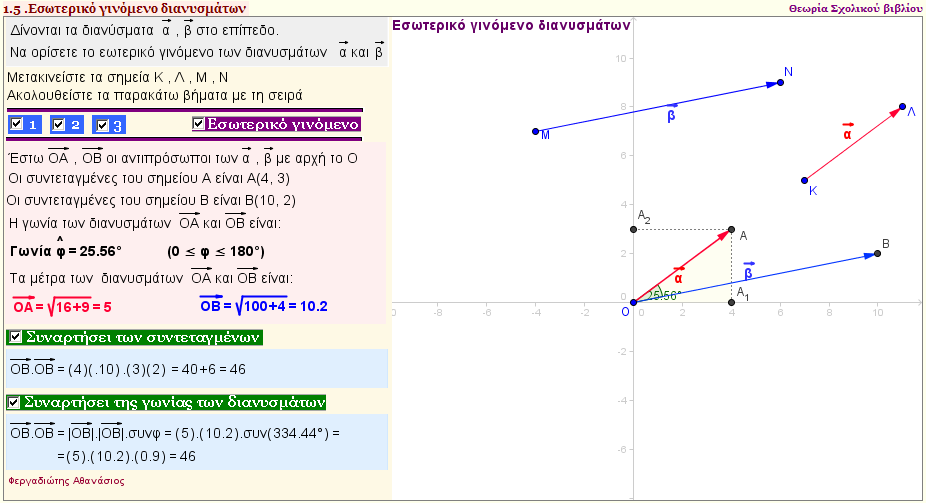
Εσωτερικό γινόμενο διανυσμάτων
Δώστε δύο διανύσματα $\vec{α}$ , $\vec{β}$ και βρείτε το εσωτερικό γινόμενο $\vec{α}$.$\vec{β}$ :
ι) Με την βοήθεια των συντεταγμένων των διανυσμάτων
ιι)Με την βοήθεια του ορισμού του εσωτερικού γινομένου
|
|
|
 |
| |
|
|
|
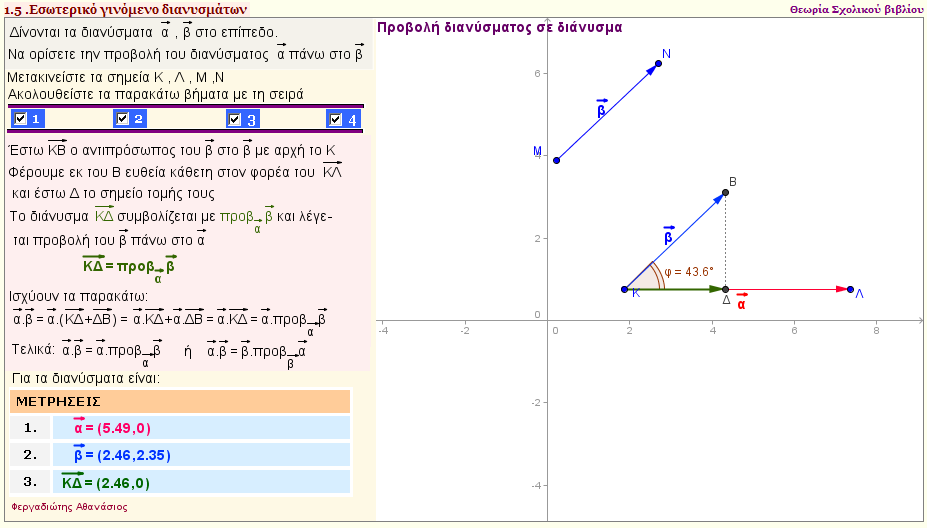
Προβολή διανύσματος σε διάνυσμα
Δώστε δύο διανύσματα $\vec{α}$ , $\vec{β}$ και βρείτε την προβολή του διανύσματος $\vec{β}$ πάνω στο $\vec{α}$
|
|
|
 |
| |
|
|
|
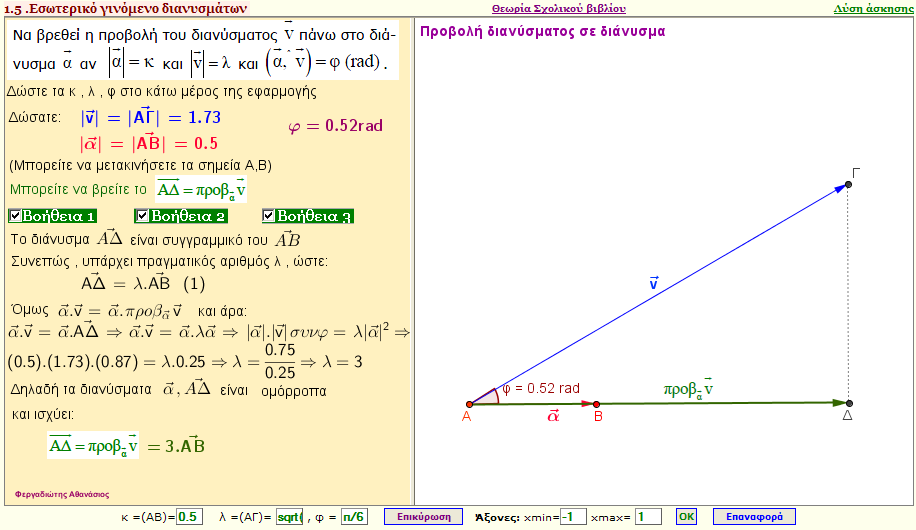
Eφαρμογή 1 - Πρόβλημα
Να βρεθεί η προβολή του διανύσματος $\vec{v}$ πάνω στο διάνυσμα $\vec{α}$ αν $|\vec{α}| = κ$ , $|\vec{v}| = λ$ και ( $\vec{α} $ , $\vec{β} $ )= φ |
|
|
 |
| |
|
|
|
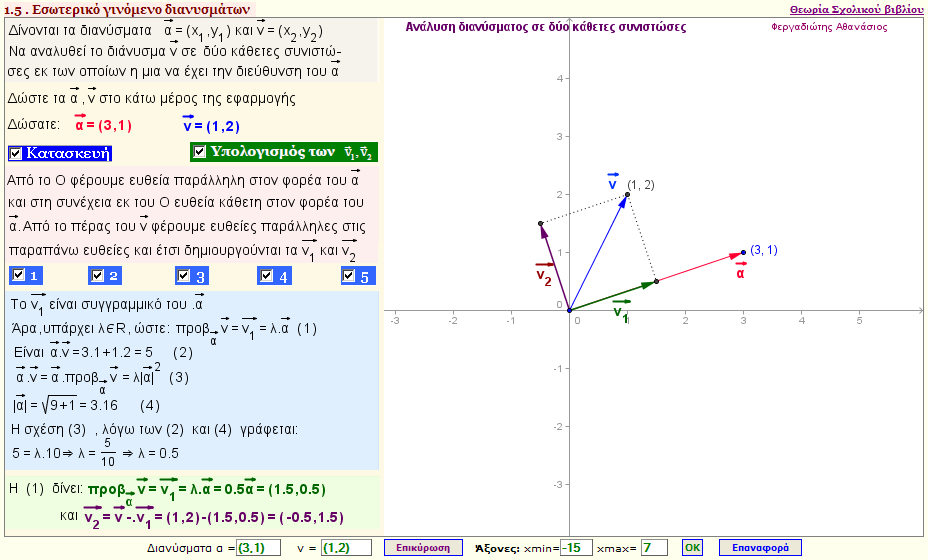
Eφαρμογή 2 - Πρόβλημα
Δίνονται τα διανύσματα $\vec{α}$ και $\vec{v}$ .Να αναλυθεί το διάνυσμα $\vec{v}$ σε δύο κάθετες συνιστώσες εκ των οποίων η μια να έχει την διεύθυνση του $\vec{α} $ . |
|
|
 |
| |
|
|
|
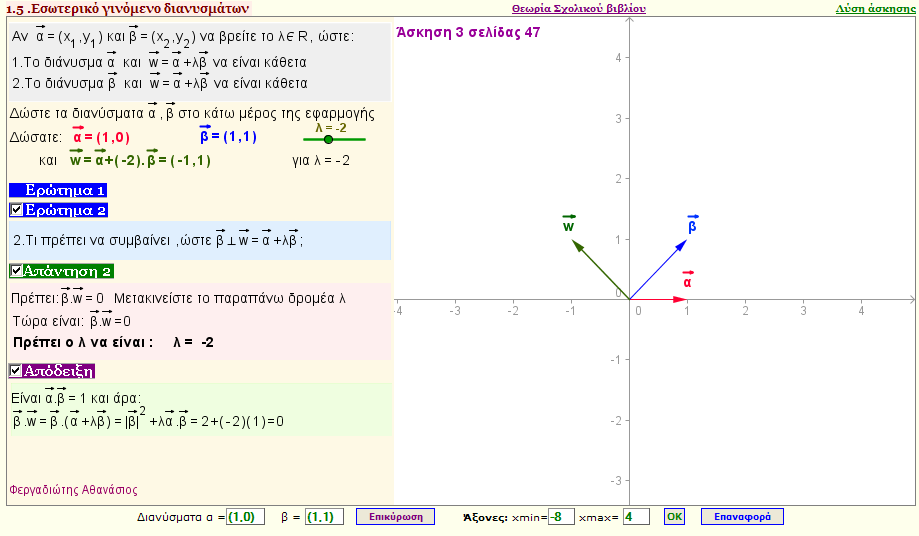
Πρόβλημα 1
Αν $\vec{α} $ =(x1 ,y1), και $\vec{β}$ =(x2 ,y2) να βρείτε το λ , ώστε:
ι)Τα διανύσματα $\vec{α}$ και $\vec{α}$ + λ$\vec{β}$ να είναι κάθετα.
ι)Τα διανύσματα $\vec{β}$ και $\vec{α}$ + λ$\vec{β}$ να είναι κάθετα.
|
|
|
 |
| |
|
|
|
Πρόβλημα 2
Αν $\vec{α} $ =(x1 ,y1), και $\vec{β}$ =(x2 ,y2) να βρείτε τα διανύσματα:
ι)Την προβολή του διανύσματος $\vec{α} $ πάνω στο $\vec{β} $ και
ιι)Την προβολή του διανύσματος $\vec{β} $ πάνω στο $\vec{α} $ |
|
|
 |
| |
|
|
|
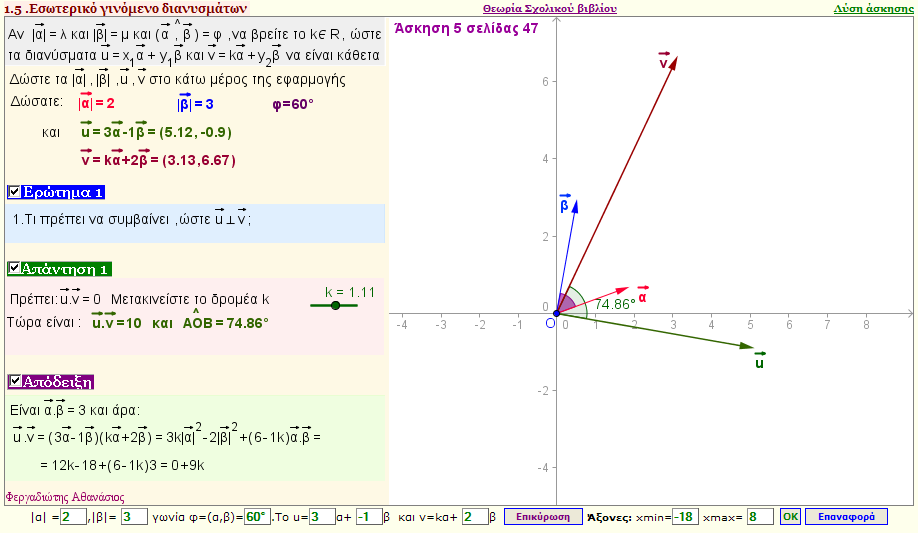
Πρόβλημα 3
Αν $|\vec{α}| $ =λ, και $|\vec{β}|$ =μ και ( $\vec{α} $ , $\vec{β} $ )= φ να υπολογίσετε τον κ$\in$R, ώστε τα διανύσματα: $\vec{u} =x1$\vec{α} + y1$\vec{β} $ και $\vec{v} = k$\vec{α} + y2$\vec{β} $ να είναι κάθετα
|
|
|
 |
| |
|
|
|
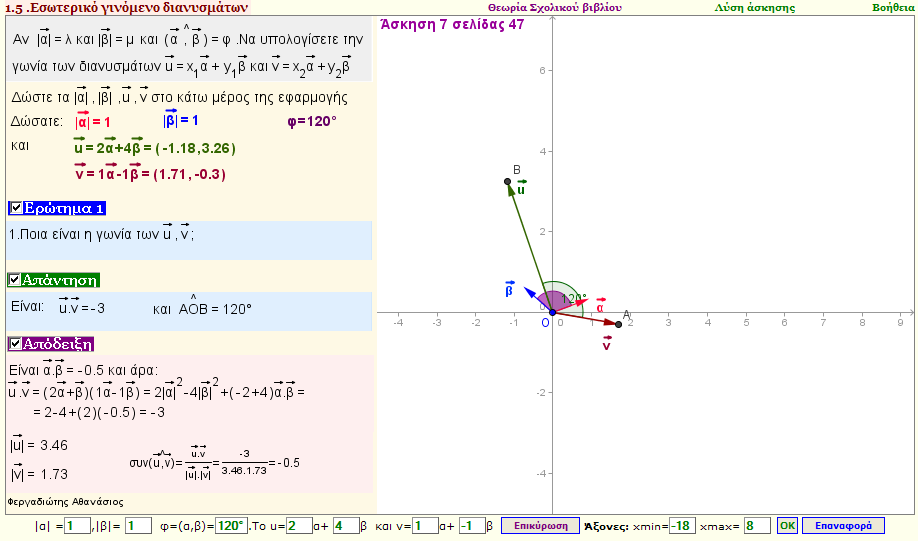
Πρόβλημα 4
Αν $|\vec{α}| $ =λ, και $|\vec{β}|$ =μ και ( $\vec{α} $ , $\vec{β} $ )= φ να υπολογίσετε την γωνία των διανυσμάτων: $\vec{u} =x1$\vec{α} + y1$\vec{β} $ και $\vec{v} = k$\vec{α} + y2$\vec{β} $ |
|
|
 |
| |
|
|
|
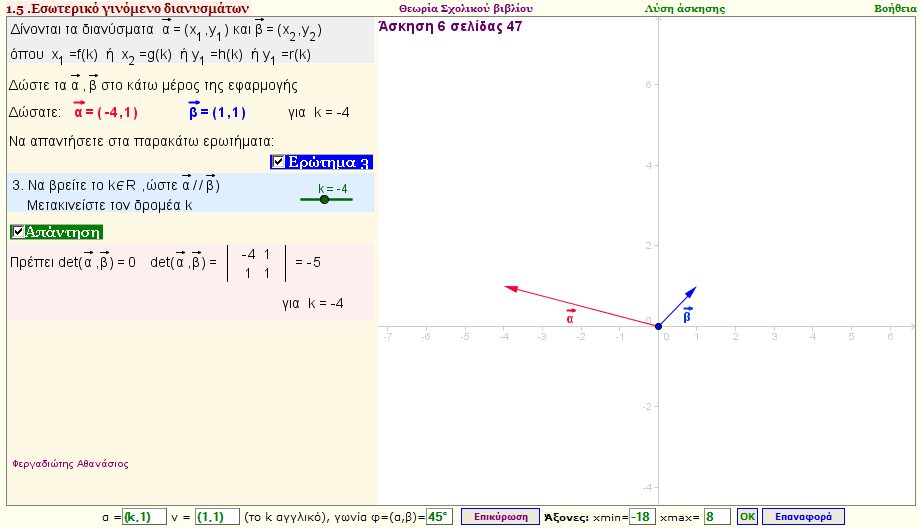
Πρόβλημα 5
Αν $\vec{α} $ =(x1,y1), και $\vec{β}$ =(x2,y2), όπου x1=f(k) , y1=g(k) ,x2=h(k) ,y2=r(k) , να υπολογίσετε το k,ώστε:
1. $\vec{α} $ .$\vec{β} $ = μ
2. ( $\vec{α} $ , $\vec{β} $ ) = φ και
3. $\vec{α} $ //$\vec{β} $ |
|
|
 |
|
|
|
B΄Λυκείου - Μαθηματικά Προσανατολισμού 
