Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση - όχημα και διαγράμματα
Η προσομοίωση εμφανίζει ένα όχημα που εκτελεί Ευθύγραμμη Ομαλά Μεταβαλλόμενη Κίνηση και ταυτόχρονα μπορεί να εμφανίσει τα διαγράμματα x-t, υ-t και α-t.

Στην προσομοίωση επιλέξτε την αρχική ταχύτητα υ0, το χρονικό διάστημα Δt, την επιτάχυνση/επιβράδυνση α, και το πρόγραμμα σχεδιάζει τις γραφικές παραστάσεις x-t, υ-t και α-t, ενώ το όχημα εκτελεί αυτή την κίνηση.
Προσομοίωση , Προσομοίωση στο Φωτόδεντρο
Αδράνεια (ip)
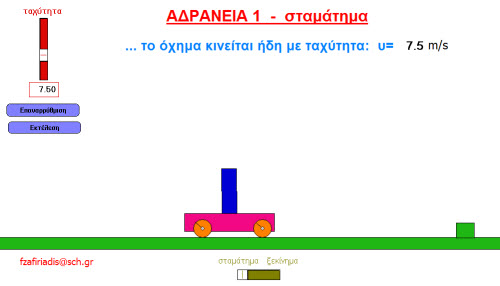
Η προσομοίωση είναι αρχείο ip και δείχνει την αδράνεια των σωμάτων (ότι θέλουν να διατηρήσουν την κινητική τους κατάσταση). Μελετάμε ένα σώμα που βρίσκεται πάνω σε ένα όχημα το οποίο είτε σταματάει απότομα ενώ κινείται, είτε ξεκινάει απότομα.
Εναλλασσόμενη τάση
Όταν ένα πλαίσιο περιστρέφεται μέσα σε ομογενές μαγνητικό πεδίο, η μαγνητική ροή του μεταβάλλεται συνεχώς και γι' αυτό δημιουργείται μια εναλλασσόμενη τάση.
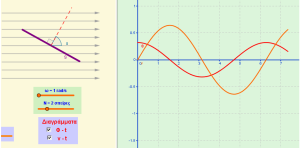
Η προσομοίωση εμφανίζει το περιστρεφόμενο πλαίσιο καθώς και τις γραφικές παραστάσεις Φ-t και v-t.
Κινούμενο πλαίσιο σε ομογενές μαγνητικό πεδίο
Θα μελετήσουμε ένα ορθογώνιο πλαίσιο που το μετακινούμε με σταθερή ταχύτητα υ προς ένα ομογενές μαγνητικό πεδίο. Το πλαίσιο εισέρχεται κάθετα στις δυναμικές γραμμές του πεδίου.
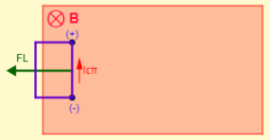
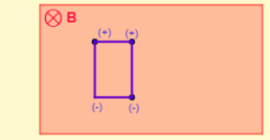
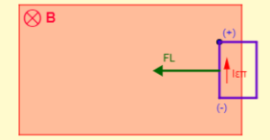
Στα σχήματα φαίνεται η είσοδος, η παραμονή και η έξοδος του πλαισίου από το μαγνητικό πεδίο.
Θα εξετάσουμε τι συμβαίνει με την μαγνητική ροή Φ που διαπερνά το πλαίσιο. Παρατηρούμε ότι αυτή μεταβάλλεται κατά την είσοδο και έξοδό του πλαισίου από το πεδίο, ενώ παραμένει σταθερή όταν όλο το πλαίσιο βρίσκεται μέσα στο πεδίο.
Εξαιτίας αυτής της μεταβολής ΔΦ κατά την είσοδο και έξοδο του πλαισίου, ταυτόχρονα συμβαίνουν τα εξής:
- αναπτύσσεται ΗΕΔ από επαγωγή
- δημιουργείται επαγωγικό ρεύμα Ιεπ (το πλαίσιο είναι ένα κλειστό κύκλωμα)
- αναπτύσσεται δύναμη Laplace FL που αντιστέκεται στην είσοδο και έξοδο του πλαισίου
- ασκείται από εμάς μια εξωτερική δύναμη Fεξ που είναι αντίθετη της δύναμης FL έτσι ώστε το πλαίσιο να κινείται με υ=σταθερό.
Κατά την παραμονή του πλαισίου μέσα στο πεδίο το Φ=σταθερό. Αυτό σημαίνει ότι:
- δεν αναπτύσσεται ΗΕΔ από επαγωγή και άρα δεν υπάρχει επαγωγικό ρεύμα Ιεπ και άρα δεν υπάρχει δύναμη FL και δεν υπάρχει εξωτερική δύναμη FL για να διατηρηθεί σταθερή η ταχύτητα του πλαισίου.
Ενδιαφέρον παρουσιάζουν οι γραφικές παραστάσεις:
- Φ-t (μαγνητική ροή Φ συναρτήσει του χρόνου t)
- Εεπ - t (ΗΕΔ από επαγωγή συναρτήσει του χρόνου t)
- Ιεπ - t (Το επαγωγικό ρεύμα που διαρρέει το πλαίσιο συναρτήσει του χρόνου t)
- FL - t (Η δύναμη Laplace συναρτήσει του χρόνου t)
- Fεξ - t (Η εξωτερική δύναμη που πρέπει να σκηθεί στο πλαίσιο συναρτήσει του χρόνου t)
Με τη προσομοίωση Geogebra κάνουμε τα εξής:
- εισάγουμε ένα ορθογώνιο πλαίσιο μέσα σε ομ. μαγνητικό πεδίο με υ=σταθερό.
- παρακολουθούμε την ΗΕΔ από επαγωγή που αναπτύσσεται στους αγωγούς του πλαισίου καθώς και το Ιεπ, τη δύναμη FL και την εξωτερική δύναμη Fεξ που του ασκείται έτσι ώστε να διατηρηθεί η ταχύτητά του.
- βλέπουμε τις αντίστοιχες γραφικές παραστάσεις των παραπάνω μεγεθών συναρτήσει του χρόνου t.
Δείτε την προσομοίωση εδώ!
Μαγνητικό πεδίο 2 ευθύγραμμων παράλληλων ρευματοφόρων αγωγών
Όταν θέλουμε να βρούμε το μαγνητικό πεδίο που δημιουργούν 2 παράλληλοι ρευματοφόροι αγωγοί σε ένα σημείο Κ, κάνουμε τα εξής:
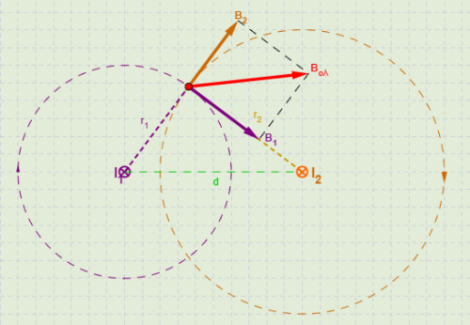
- Σχεδιάζουμε τους αγωγούς έτσι ώστε αυτοί να είναι κάθετοι στο επίπεδο της οθόνης.
- Δηλώνουμε τις φορές των ρευμάτων που διαρρέουν τους αγωγούς.
(Στο σχήμα μας έχουμε 2 αγωγούς που διαρρέονται από ομόρροπα ρεύματα Ι1 και Ι2 που έχουν φορά από εμάς προς το εσωτερικό της οθόνης). - Για τον αγωγό Ι1 σχεδιάζουμε ένα μικρό τμήμα κύκλου που να περνάει από το σημείο Κ και με τον κανόνα του δεξιού χεριού βρίσκουμε τη κατεύθυνση της δυναμικής γραμμής.
- Σχεδιάζουμε το διάνυσμα Β1 που είναι εφαπτόμενο στο κύκλο και έχει τη κατεύθυνση της δυναμικής γραμμής.
- Το ίδιο ακριβώς κάνουμε και για τον αγωγό Ι2 ο οποίος τελικά στο σημείο Κ δημιουργεί ένα διάνυσμα Β2.
Για να βρούμε το συνολικό μαγνητικό πεδίο στο σημείο Κ αρχικά προσθέτουμε διανυσματικά τα διανύσματα Β1 και Β2, δηλαδή απλώς στο σχήμα με τον κανόνα του παραλληλογράμμου σχεδιάζουμε το διάνυσμα Βολ.
Ο υπολογισμός του μέτρου του Βολ γίνεται με τη γνωστή σχέση:
Με τη προσομοίωση Geogebra κάνουμε τα εξής:
- σχεδιάζουμε 2 αγωγούς κάθετους στην οθόνη και επιλέγουμε φορά και τιμή ρεύματος
- σχεδιάζουμε τις δυναμικές γραμμές και τα διανύσματα Β1 και Β2.
- εμφανίζουμε το διάνυσμα της Βολ και υπολογίζουμε το μέτρο του.