Ο Αρχιμήδης ζυγίζει σχήματα

Καὶ γάρ τινα τῶν πρότερόν μοι φανέντων μηχανικῶς ὕστερον γεωμετρικῶς ἀπεδείχθη διὰ τὸ χωρὶς ἀποδείξεως εἶναι τὴν διὰ τούτου τοῦ τρόπου θεωρίαν∙ ἑτοιμότερον γάρ ἐστι προλαβόντα διὰ τοῦ τρόπου γνῶσίν τινα τῶν ζητημάτων πορίσασθαι τὴν ἀπόδειξιν μᾶλλον ἤ μηδενὸς ἐγνωσμένου ζητεῖν. Άλλωστε κάποιες ιδιότητες που στην αρχή μου αποκαλύφθηκαν με τη μηχανική στη συνέχεια αποδείχθηκαν με τη γεωμετρία, διότι η προσέγγιση που γίνεται με τη μέθοδο αυτή δεν επιδέχεται απόδειξης. Είναι ευκολότερο να οδηγηθείς στην απόδειξη, εάν έχεις αποκτήσει εκ των προτέρων κάποια γνώση του πράγματος, παρά αν ψάχνεις κάτι για το οποίο δεν έχεις την παραμικρή ιδέα. Αρχιμήδης, Περί των μηχανικών θεωρημάτων προς Ερατοσθένην έφοδος

Το επιστημονικό έργο του Αρχιμήδη είναι πραγματικά εντυπωσιακό: Θεματολογικός πλούτος, πρωτότυπες μέθοδοι που ανήκουν περισσότερο στο μέλλον παρά στην εποχή του, μαθηματική ακρίβεια. Δίκαια οι μελετητές του τον θεωρούν έναν από τους τρεις ευφυέστερους ανθρώπους που γέννησε η ανθρωπότητα ανά τους αιώνες, αν ίσως όχι τον μεγαλύτερο. Πώς όμως συνέλαβε τις ιδέες του; Από τα συγγράμματα που μάς άφησε καταλαβαίνουμε πως ήταν ιδιαίτερα τολμηρός και με πλούσια φαντασία.

Στο παρόν άρθρο θα σκιαγραφήσουμε ένα τέτοιο τόλμημα, που εμένα προσωπικά με εξέπληξε τρομερά: Προκειμένου να υπολογίσει το εμβαδόν παραβολικού τμήματος, φαντάζεται πως αυτό έχει υλική υπόσταση, εξισορροπώντας σε ζυγό το βάρος του με το βάρος γνωστού τριγώνου.

Το θέμα είναι από το έργο του "Τετραγωνισμός παραβολής" και αποτελεί την μηχανική προσέγγιση του υπολογισμού του εμβαδού παραβολικού τμήματος, όπου αποκτάται η "θεωρία" για τον υπολογισμό και προηγείται της γεωμετρικής αυστηρής απόδειξης που εκτίθεται στη συνέχεια, χωρίς όμως να θεωρείται υποδεέστερη.

Για περισσότερη μελέτη προτείνουμε:

• Η μέθοδος της εξάντλησης των Ευδόξου-Αρχιμήδη, διπλωματική εργασία του Βασιλείου Ν. Γεωργίου
• Τετραγωνισμός παραβολής, από τα "Μαθηματικά των Ελλήνων"

Σημεία ανάπτυξης:

• Η ζητούμενη σχέση παραβολικού τμήματος και τριγώνου
• Βασικές γεωμετρικές σχέσεις
• Το κεντρικό θεώρημα με την ισορροπία του ζυγού
• Με σύγχρονη μαθηματική γλώσσα
• Δυναμική αναπαράσταση του επιχειρήματος

Η ζητούμενη σχέση παραβολικού τμήματος και τριγώνου

Το παραβολικό τμήμα είναι το φραγμένο χωρίο που ορίζεται από μια τέμνουσα ευθεία και την παραβολή. Βάση του παραβολικού τμήματος θεωρείται το ευθύγραμμο τμήμα που έχει άκρα τα σημεία τομής της τέμνουσας ευθείας και της παραβολής (το ΑΓ στο σχήμα), ενώ κορυφή του είναι εκείνο το σημείο της παραβολή που η εφαπτομένη σε αυτό είναι παράλληλη στην βάση (στο σχήμα το σημείο Β). Ακόμα, ο άξονας συμμετρίας της παραβολής καλείται και διάμετρος της παραβολής. Ο Αρχιμήδης αποδεικνύει ότι το εμβαδόν ενός παραβολικού τμήματος είναι τα 4/3 του εμβαδού του τριγώνου που έχει την ίδια βάση και την ίδια κορυφή (Πρόταση 1). Στο σχήμα δηλαδή, το εμβαδόν του παραβολικού τμήματος ΑΒΓ (γαλάζια περιοχή) είναι τα 4/3 του εμβαδού του τριγώνου ΑΒΓ. Επεξηγηματικά για το σχήμα: Οι γαλάζιες ευθείες είναι η μία ο άξονας συμμετρίας της παραβολής και η άλλη η εφαπτομένη στο σημείο Β, κορυφή του τμήματος.

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας

Βασικές γεωμετρικές σχέσεις

Αν μας δώσουν ένα παραβολικό τμήμα με βάση ΑΓ και κορυφή Β (διπλανό σχήμα), και φέρουμε ευθεία παράλληλη προς την διάμετρο της παραβολής από το σημείο Α και την εφαπτομένη της παραβολής στο σημείο Γ, τότε αυτές τέμνονται σε σημείο Ζ, ορίζοντας ένα μεγαλύτερο τρίγωνο ΑΓΖ. Αν επιπλέον φέρουμε παράλληλη ευθεία προς τη διάμετρο της παραβολής από το σημείο Β (κορυφή), αυτή τέμνει την ΑΓ στο Δ και την ΖΓ στο Ε και ισχύει: ΑΔ = ΔΓ (δηλαδή το Δ είναι το μέσο του ΑΓ) ΒΔ = ΒΕ (δηλαδή το Β είναι το μέσο του ΔΕ) Συνεπώς, Το Ε είναι μέσο του ΖΓ (αφού ΑΖ // ΔΕ και Δ είναι μέσο του ΑΓ) (ΑΒΓ) = 2(ΒΔΓ) = (ΕΔΓ) = (ΖΓΔ)/4 Όπου με παρενθέσεις συμβολίζουμε τα εμβαδά των τριγώνων Σχόλιο: Θα ήταν ενδιαφέρον να αποδείξει κάποιος τις δύο πρώτες σχέσεις παραπάνω, με γεωμετρικές ή αναλυτικές μεθόδους. Κάποια ιδέα σάς δίνει το κείμενο εδώ. Ακόμα καλύτερα, διαβάστε το άρθρο Archimedes Triangle and Squaring of Parabola από το cut-the-knot.

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας

To κεντρικό θεώρημα με την ισορροπία του ζυγού

Στη συνέχεια, ο Αρχιμήδης παίρνει μια τυχαία διατομή ΞΜ του τριγώνου ΖΑΓ, παράλληλη στην ΑΓ, που τέμνει την προέκταση της ΓΒ στο Ν και την παραβολή στο Ο. Χρησιμοποιώντας τη γνωστή σχέση 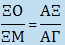σε συνδυασμό με την επόμενη αναλογία, που ισχύει λόγω των παραλλήλων ΖΑ, ΜΞ που τέμνονται από τις ΓΚ και ΓΑ, 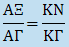παίρνει: 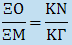Έπειτα, προεκτείνει την ΓΚ κατά ίσο τμήμα ΚΘ και σχεδιάζει τμήμα ΤΗ = ΟΞ, με το Θ στο μέσο του. Τότε η προηγούμενη σχέση γίνεται

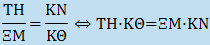Όμως, τα σημεία Θ και Ν είναι τα μέσα των τμημάτων ΤΗ και ΜΞ αντίστοιχα (το Ν είναι μέσο του ΜΞ, αφού το Β είναι μέσο του ΔΕ), επομένως, η προηγούμενη σχέση δηλώνει μια σχέση ισορροπίας των τμημάτων ΤΗ και ΜΞ, αν τα φανταστούμε με υλική υπόσταση, να εξισορροπούν σε νοητό ζυγό με φάλαγγα το ΘΝ (που θα οριζοντιοποιηθεί όταν επέλθει η ισορροπία) και κέντρο ισορροπίας το σημείο Κ.

Εξασφαλίζοντας την ισορροπία κάθε διατομής ΜΞ του τριγώνου ΑΖΓ, που είναι παράλληλη στην ΑΓ, με την αντίστοιχη διατομή ΟΞ της παραβολής (στη θέση ΤΗ), προχωρά στην εξισορρόπηση ολόκληρου του παραβολικού τμήματος ΑΒΓ με το τρίγωνο ΑΖΓ, μεταφέροντας το παραβολικό τμήμα σε θέση έτσι ώστε το κέντρο βάρος του να είναι στο σημείο Θ. Καθώς το κέντρο βάρος του τριγώνου ΑΖΓ είναι σημείο Χ της ΚΓ και επειδή έτσι τα δύο σχήματα ισορροπούν σε ζυγό φάλαγγας ΘΧ με κέντρο ισορροπίας το Κ, θα έχουμε:

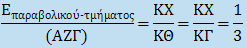
Όμως, όπως είδαμε στην αρχή, (ΑΖΓ) = 4(ΑΒΓ), επομένως,

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας

Με σύγχρονη μαθηματική γλώσσα

Ο Αρχιμήδης προβάλει το παραπάνω επιχείρημα μόνο ως ευρετική μέθοδο, μια μέθοδο δηλαδή που τού αποκαλύπτει την σχέση εμβαδών του παραβολικού τμήματος και του τριγώνου με την ίδια βάση και κορυφή. Θα συνεχίσει μετά από αυτό, με ένα πιο αυστηρά γεωμετρικό επιχείρημα, που όλοι λίγο-πολύ γνωρίζουμε ως "μέθοδο εξάντλησης".

Όπως αναφέρει και στην διπλωματική του μελέτη ο Βασίλειος Γεωργίου, μια απάντηση στο "γιατί ο Αρχιμήδης δεν θεωρεί επαρκή την ευρετική του μέθοδο" που δόθηκε από τον Γ. Χριστιανίδη, είναι η έλλειψη μαθηματικής αυστηρότητας που γίνεται με την χρήση των "αδιαιρέτων", δηλαδή των διατομών των σχημάτων με ευθείες και όχι γιατί χρησιμοποιεί μηχανικές μεθόδους (ζυγίσματα).

Κι όμως, τα "αδιαίρετα" του Αρχιμήδη είναι αυτά που χρησιμοποιούνται στις σύγχρονες μεθόδους. Τόσο το εμβαδόν ενός επίπεδου σχήματος, όσο και το κέντρο βάρος του, ορίζονται με την ίδια ακριβώς μέθοδο, της δόμισης και αποδόμισης του σχήματος από τις διατομές του.

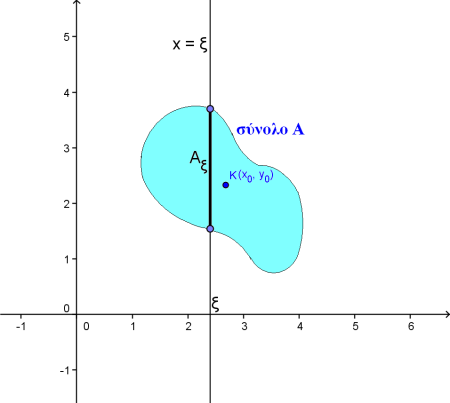Για να καταλάβουμε το πώς, ας πάρουμε ένα τυχαίο ευθύγραμο σχήμα, έστω το σύνολο Α του διπλανού σχήματος, που έχει κέντρο βάρους το σημείο Κ(x0, y0). Για κάθε ξ στον άξονα x'x παίρνουμε την διατομή του Α με την ευθεία x=ξ, που ας την ονομάσουμε Aξ. Τότε, αν συμβολίσουμε με |Α| το εμβαδόν του Α και με |Aξ| το μήκος του Aξ ισχύει ότι: 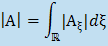Ακόμα, οι συντεταγμένες του κέντρου βάρους Κ, μπορούν να εκφραστούν με ένα ολοκλήρωμα, που εξάγεται από την συνθήκη ισορροπίας που χρησιμοποίησε ο Αρχιμήδης. Ειδικότερα για το x0 έχουμε:

Στο επιχείρημα του Αρχιμήδη, αν πούμε x₀ την τετμημένη του Χ, ξ την τετμημένη του Ξ, κ την τετμημένη του Κ και θ την τετμημένη του Θ, η σχέση ισορροπίας ΤΗ*ΚΘ=ΞΜ*ΚΝ είναι ισοδύναμη με την ΤΗ(κ-θ)=ΞΜ(ξ-κ), που αλλιώς, με τον συμβολισμό που θέσαμε προηγουμένως, γράφεται

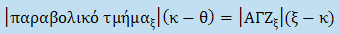
Και εδώ, ο δείκτης ξ δηλώνει την αντίστοιχη διατομή. Ολοκληρώνοντας (για να αναδομίσουμε τα σχήματα) παίρνουμε το ζητούμενο:

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας

Δυναμική αναπαράσταση του επιχειρήματος

Μπορείτε να μελετήσετε το μηχανικό επιχείρημα καλύτερα, χρησιμοποιώντας την java εφαρμογή που δημιουργήθηκε με το πρόγραμμα δυναμικής Γεωμετρίας GeoGebra.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας