Κανονικά πολύγωνα και γρίφοι χαρτοδιπλωτικής

Η τυχερή μου μέρα

Η μητέρα μου, μού έδειξε κάποτε το φοιτητικό της λεύκωμα με τα γεωμετρικά μοτίβα, που είχε ετοιμάσει ως σπουδάστρια της Παιδαγωγικής Ακαδημίας Ηρακλείου. Έμεινα κατάπληκτη! Τι ομορφιά! Τι σοφία! Όποιος τα σκέφτηκε, είχε καλαισθησία και μαθηματική ευφυΐα μαζί! Σε κάθε μοτίβο επαναλαμβανόταν μια ψηφίδα, που ήταν ιδιαίτερη, είτε για τις «έξυπνες» διπλώσεις της, είτε για τα πολύχρωμα γλασέ χαρτιά και χρυσαφένια, είτε για το πλέξιμο που έκανε με τις άλλες ψηφίδες και το φόντο.

Το ενδιαφέρον μου προσήλκυσε ένα μοτίβο με τετραγωνικές ψηφίδες που όμως γεννήθηκαν από την δίπλωση κυκλικού δίχρωμου γλασέ χαρτιού. Τι άλλο εκτός από τετράγωνο θα μπορούσε να «γεννήσει» ένα κυκλικό χαρτί; Μήπως κανονικό εξάγωνο ή ισόπλευρο τρίγωνο; Έτσι, συνέλαβα τον εαυτό μου να καταγίνεται με τον σχηματισμό πολυγωνικών ψηφίδων, διπλώνοντας κυκλικά χαρτιά.

Ομολογώ, πως το πόνημα ήταν πραγματικά δύσκολο. Ενώ μια χαρά γνώριζα το πώς εγγράφω κανονικό εξάγωνο σε κύκλο, χρησιμοποιώντας κανόνα και διαβήτη, γιατί εγώ ήθελα να το επιτύχω αυτό μονάχα με διπλώσεις, χωρίς καθόλου γεωμετρικά όργανα; Τελικά, τα κατάφερα γιατί σκέφτηκα μαθηματικά.

Πλέον, ήμουν σίγουρη πως για να εγγράψει κάποιος ένα κανονικό εξάγωνο σε κύκλο, με τους κανόνες της χαρτοδιπλωτικής, θα παρήγαγε μαθηματικά. Τότε, για πρώτη φορά αντιλήφθηκα τον πλήρη παραλληλισμό της γεωμετρικής κατασκευής με κανόνα και διαβήτη και της γεωμετρικής κατασκευής με τους κανόνες της χαρτοδιπλωτικής. Γιατί η χαρτοδιπλωτική εκμεταλλεύεται την αξονική συμμετρία για να κατασκευάσει διχοτόμους, διαμέσους, μεσοκαθέτους κ.α.

Αυτήν την αίσθηση, θέλησα να την μεταδώσω και στους μαθητές μου. Έτσι, αποφάσισα να διαμορφώσω την ιδέα σε μάθημα: Εγγραφή κανονικών πολυγώνων σε κύκλο, με τους κανόνες της χαρτοδιπλωτικής. Το μάθημα υλοποιήθηκε (τμήμα Β₃, Π.Γ.Λ.Η. 2008-09) και ήταν ένα από τα πιο πετυχημένα μαθήματα της διδακτικής μου πορείας! Ας δούμε μαζί την περιπέτειά του:

Σημεία ανάπτυξης

• Το αισθητικό ερέθισμα
• Ο γρίφος του τετραγώνου
• Ο γρίφος του κανονικού εξαγώνου
• Ο γρίφος του ισόπλευρου τριγώνου
• Οι δημιουργίες της μητέρας μου

Το αισθητικό ερέθισμα

Το μάθημα θα λάμβανε χώρα την ώρα της Γεωμετρίας Β' Λυκείου, όπου ένα θέμα είναι η γεωμετρική εγγραφή βασικών κανονικών πολυγώνων σε κύκλο. Η βασική ιδέα του μαθήματος, ήταν να διέλθουν οι μαθητές μου από όλα τα στάδια μάθησης που διήλθα κι εγώ, δηλαδή,

1. Να συγκινηθούν από ένα ολοκληρωμένο κολλάζ ψηφίδων και να γεννηθεί φυσικά το ερώτημα για τον τρόπο κατασκευής των ψηφίδων
2. Να ανακαλύψουν μόνοι τους, χωρίς την δική μου βοήθεια, τον τρόπο κατασκευής
3. Να συνειδητοποιήσουν τα μαθηματικά που χρησιμοποίησαν
4. Να συνθέσουν τα δικά τους δημιουργήματα

Από τα παραπάνω, το τελευταίο δυστυχώς δεν μπόρεσα να το επιτύχω, ελλείψει χρόνου (διέθεσα μία μόνο διδακτική ώρα). Όμως, επειδή πραγματικά οι μαθητές μου ανακάλυψαν ΜΟΝΟΙ ΤΟΥΣ τον τρόπο κατασκευής των ψηφίδων, η χαρά και η ικανοποίησή τους ήταν πολύ μεγάλη και αυτό κάλυψε το κενό της εικαστικής δημιουργίας.

Χρησιμοποιώντας δίχρωμα χαρτιά (κόλλες γλασέ ή χαρτιά περιτυλίγματος) σχημάτισα με ένα CD κύκλους, που τους έκοψα, τους δίπλωσα, τους κόλλησα, για να σχηματίσω τις ψηφίδες και τις συνθέσεις που έδειξα στους μαθητές μου. Μπορείτε να τις δείτε παρακάτω και με "κλικ" επάνω τους να τις μεγεθύνετε.

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας

Ο γρίφος του τετραγώνου

Το επόμενο στάδιο αφορούσε την εμπλοκή των ίδων των μαθητών. Σε κάθε θρανίο έδωσα ένα δίχρωμο κυκλικό χαρτί με την πρόκληση να συνεργαστούν για να κατασκευάσουν ΜΟΝΟ με διπλώσεις ένα εγγεγραμμένο τετράγωνο.

Σχεδόν αμέσως, όλα τα ζευγάρια είχαν επιτύχει το ποθούμενο. Δίπλωσαν τον κύκλο στην μέση και μετά το ημικύκλιο πάλι στη μέση. Έτσι, διαιρέθηκε ο κύκλος σε τέσσερα ίσα τόξα. Οι χορδές τους, που διπλώθηκαν στη συνέχεια, ήταν οι πλευρές του ζητούμενου τετραγώνου.

Άραγε, όταν οι μαθητές μου δίπλωναν και ξανά-δίπλωναν τον κύκλο, είχαν καθόλου στο νου τους ότι "αν κάποια σημεία διαιρούν τον κύκλο σε ίσα τόξα, τότε αυτά είναι κορυφές κανονικού πολυγώνου";

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας

Ο γρίφος του κανονικού εξαγώνου

Ο δεύτερος γρίφος, να δημιουργήσουν ένα κανονικό εξάγωνο εγγεγραμμένο στον κύκλο, τους παίδεψε πραγματικά πολύ. Χρειάστηκε να τους δώσω και ξαναδώσω κυκλικά χαρτιά για να ξαναρχίσουν τις προσπάθειες. Έριχναν ματιές δεξιά-αριστερά, αλλά τίποτα! Κάποια στιγμή είπα να τους βοηθήσω λίγο, όμως ήθελα πολύ να ανακαλύψουν μόνοι τους την μέθοδο δίπλωσης. Ίσως να τους επεσήμανα ότι με την προηγούμενη κατασκευή του τετραγώνου, γνώριζαν ήδη έναν τρόπο να προσδιορίσουν με ακρίβεια το κέντρο του κύκλου.

Και το «θαύμα» έγινε από εκεί που δεν το περίμενα: Την ανακάλυψη την έκανε μια έξυπνη μαθήτρια, αλλά όχι ιδιαίτερα επιμελής. Αμέσως, οι συμμαθητές της έτρεξαν δίπλα της, λαχταρώντας να μάθουν το πώς. Έτσι όχι εγώ, αλλά μια συμμαθήτριά τους τούς δίδαξε πώς να εγγράφουν κανονικό εξάγωνο σε κύκλο, με διπλώσεις και μόνο.

Αλλά ας δούμε την ιδέα βήμα-βήμα και τα μαθηματικά που κρύβει:

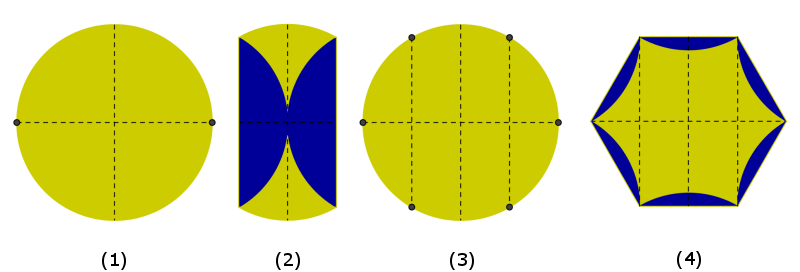
• Σχήμα (1): Ξεκινάμε, έχοντας τσακίσει δύο κάθετες διαμέτρους, ώστε να έχει προσδιοριστεί το κέντρο του κύκλου, αλλά και δύο αντιδιαμετρικά σημεία του.
• Σχήμα (2): Μεταφέρουμε τα δύο αντιδιαμετρικά σημεία στο κέντρο του κύκλου και τσακίζουμε.
• Σχήμα (3): Με την προηγούμενη τσάκιση δημιουργήθηκαν οι μεσοκάθετοι των δύο ακτίνων και τα σημεία τομής τους με τον κύκλο (δηλαδή δημιουργήθηκαν 4 καινούρια σημεία). Καθένα από τα τέσσερα νέα σημεία, ως σημείο μεσοκαθέτου, απέχει εξίσου από ένα από τα δύο αρχικά σημεία του κύκλου και από το κέντρο του κύκλου. Έτσι, το εγγεγραμμένο εξάγωνο που έχει κορυφές τα 4 καινούρια σημεία και τα 2 αρχικά, έχει όλες του τις πλευρές ίσες με μια ακτίνα, επομένως είναι κανονικό εξάγωνο.
• Σχήμα (4): Διπλώνουμε τις πλευρές του κανονικού εξαγώνου για να το σχηματίσουμε.

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας

Ο γρίφος του ισόπλευρου τριγώνου

Αν κάποιος γνωρίζει τον τρόπο κατασκευής του κανονικού εξαγώνου, τότε, δεν θα δυσκολευτεί να βρει τον τρόπο κατασκευής του ισόπλευρου τριγώνου. Μένει να κάνει ακόμα δύο τσακίσεις (πρώτο σχήμα στην επόμενη εικόνα), έτσι ώστε να συνδέσει μία-παρά-μία τις κορυφές του εξαγώνου.

Αν διπλώσουμε αντίθετα τις πλευρές του τριγώνου από τις πλευρές του εξαγώνου, θα πάρουμε μια εντυπωσιακή ψηφίδα, όπως φαίνεται στο δεύτερο σχήμα παρακάτω.

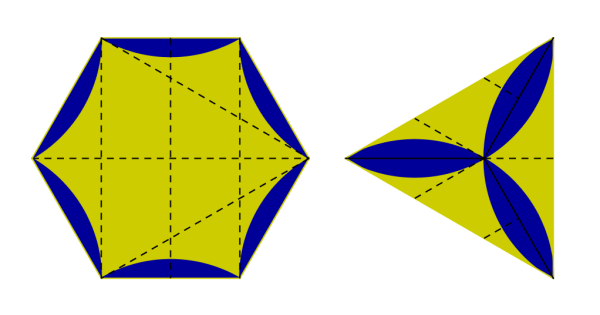
Ας σχολιάσω μόνο ότι η δίπλωση του εξαγώνου σε τρίγωνο, καθιστά ιδιαίτερα εμφανείς τις εξής ιδιότητες των σχημάτων: Το εξάγωνο έχει διπλάσιο εμβαδόν από το τρίγωνο, το απόστημα του τριγώνου είναι μισή ακτίνα.

Ακόμα, η δίπλωση των κυκλικών τμημάτων, δημιουργεί καμπυλόγραμμα σχέδια που οι μαθητές θα δουν σε επόμενο κεφάλαιο για τον υπολογισμό του εμβαδού τους. Έτσι, εξοικειώνονται με την ανάλυση ενός σύνθετου σχεδίου σε απλούστερα, όπως πολύγωνα, κυκλικούς τομείς ή τμήματα, δεξιότητα ιδιαίτερα χρήσιμη.

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας

Οι δημιουργίες της μητέρας μου

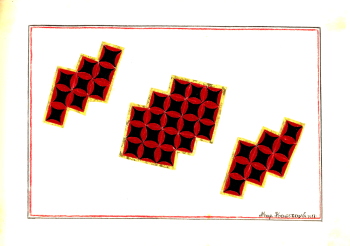
Μοιράζομαι μαζί σας τα έργα της μητέρας μου, που αποτέλεσαν την έμνευσή μου. Πιστεύω κι εσείς θα τα βρείτε ενδιαφέροντα. Κάνοντας "κλικ" επάνω τους, μπορείτε να τα δείτε σε μεγέθυνση.

Οι γονείς μου, Απρίλιος 2010

Κατάλογος με τα σημεία ανάπτυξης
Αρχή της σελίδας