Ανδρέας Ιωάννου Κασσέτας

Η έννοια ΚΕΝΤΡΟ ΜΑΖΑΣ

1. Η οικοδόμηση της έννοιας

Γεωμετρικό σημείο με ιδιαίτερη σημασία

Στη Mechanica του 1736, ο Euler αποδίδει ιδιαίτερη σημασία στο γεωμετρικό σημείο ΚΕΝΤΡΟ ΜΑΖΑΣ . Για κάθε μηχανικό στερεό ορίζει ένα ΚΕΝΤΡΟ ΜΑΖΑΣ σε αναλογία με το center of gravity – κέντρο βάρους - του Isaac Newton, αποσαφηνίζοντας και τη μεταξύ τους εννοιακή διαφορά. Θεωρεί ότι δύο γεωμετρικά αυτά σημεία συμπίπτουν εφόσον το σώμα υφίσταται τη δράση της βαρύτητας ή - με μεταγενέστερους όρους - βρίσκεται σε ομογενές πεδίο βαρύτητας . Θεωρεί όμως ότι το κέντρο μάζας έχει μεγαλύτερο εννοιακό πλάτος δεδομένου ότι αναφέρεται στην αδράνεια του σώματος και θα υφίσταται ως έννοια ακόμα και αν το σώμα δεν υφίσταται τη δράση της βαρύτητας οπότε το κέντρο βάρους ως έννοια δεν υφίσταται.

Οι Γάλλοι θα προτιμήσουν τον όρο centre d’ inertie – κέντρο αδράνειας.

Η θέση του .

Θεωρητικά η θέση του κέντρου μάζας προσδιορίζεται με αξιοποίηση της έννοιας ροπή δύναμης και του θεωρήματος των ροπών.

Αν τα υλικά σημεία βρίσκονται σε μία ευθεία και θεωρήσουμε σύστημα αναφοράς με άξονα x να συμπίπτει με την ευθεία αυτή, η θέση του κέντρου μάζας προσδιορίζεται με το θεώρημα των ροπών, με βάση τη λογική ότι η ολική ροπή, ως προς Ο, των δυνάμεων βάρους για καθένα θα είναι ίση με τη ροπή του βάρους του συστήματος προκύπτει ότι για τη θέση x_cm του κέντρου μάζας ισχύει

m₁gx₁ + m₂gx₂ + m₃gx₃ + . . m_ngx_n = (m₁+ m₂ +m₃ + . . m_n)gx_cm .

x_cm = (m₁x₁ + m₂x₂ + . . + m_nx_n )/ (m₁+ m_{2 .} . . . + m_n)

Για ένα σύνολο υλικών σημείων στη γενική περίπτωση ή για ένα στερεό με τρεις διαστάσεις οι εξισώσεις για τις τρεις συντεταγμένες ( x_cm, y_cm , z_cm ) του κέντρου μάζας είναι αντίστοιχες με την παραπάνω .

Αν ένα ομογενές σώμα ομογενές έχει σχήμα τέτοιο ώστε να διαθέτει δύο τουλάχιστον τεμνόμενους άξονες συμμετρίας, το κέντρο μάζας είναι το σημείο τομής τους. Το παράδειγμα του σώματος σε σχήμα ορθού παραλληλεπιπέδου, κυλίνδρου, δακτυλίου, σφαίρας.

Πειραματικά η θέση του κέντρου μάζας προσδιορίζεται αν αναρτήσουμε το σώμα με κατακόρυφο νήμα , το αφήσουμε να ισορροπήσει και 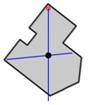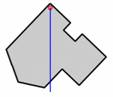χαράξουμε πάνω του την προέκταση της ευθείας του νήματος και στη συνέχεια επαναλάβουμε τη διαδικασία αναρτώντας το σώμα από άλλο σημείο του χαράσσοντας την αντίστοιχη προέκταση του νήματος. Το σημείο τομής των δύο ευθειών που χαράξαμε είναι το κέντρο βάρους, άρα και το κέντρο μάζας .

Εξυπακούεται ότι η προτεινόμενη μέθοδος δεν είναι η μοναδική

Ορμή ενός συστήματος και κέντρο μάζας.

Κατά τη θεμελίωση της Μηχανικής έχει αποδειχθεί η έννοια κέντρο μάζας παίζει έναν ιδιαίτερο ρόλο στον προσδιορισμό της ορμής ενός συστήματος. Συγκεκριμένα αποδεικνύεται ότι η ορμή ενός συστήματος – διανυσματικό άθροισμα των ορμών - είναι ίση με το γινόμενο της μάζας του συστήματος επί την ταχύτητα του κέντρου μάζας

Θεώρημα του κέντρου μάζας .

Ο Euler, με αφετηρία τον αναφερόμενο σε υλικό σημείο δεύτερο νευτωνικό νόμο της κίνησης προτείνει τους νόμους για τη Μηχανική κάθε corpus rigidus μέσα από διαφορικές εξισώσεις.

O λεγόμενος «πρώτος νόμος του Euler » αναφερόμενος σε οποιαδήποτε κίνηση οποιουδήποτε σώματος προτείνει να αποδεχτούμε ότι η ασκούμενη στο σώμα ολική εξωτερική δύναμη είναι , σε κάθε χρονική στιγμή, ίση με τον ρυθμό μεταβολής της ορμής του σώματος τη στιγμή εκείνη, περιγράφοντας τον στιγμιαίο ρυθμό μεταβολής της ορμής με τη χρονική παράγωγο της τιμής της αντίστοιχης συνάρτησης p = p(t)

F_εξ = dp/dt F = d(mυ_cm)/dt

Για την ειδική περίπτωση όπου η μάζα είναι χρονικά σταθερή F_εξ = mdυ_cm/dt F_εξ = mα_cm

Από τον νόμο αυτό, εκτός των άλλων, προκύπτει και ότι :

Καθώς κινείται ένα corpus rigidus μάζας m οποιαδήποτε και να είναι η μορφή της κίνησης του, το γεωμετρικό σημείο ΚΕΝΤΡΟ ΜΑΖΑΣ θα εκτελεί την κίνηση που θα εκτελούσε ένα σημειακό αντικείμενο μάζας m εάν σε αυτό δρούσαν οι εξωτερικές δυνάμεις οι οποίες ασκούνται στο σώμα .

Η πρόταση αναφέρεται και ως θεώρημα του κέντρου μάζας .

Ασκούμενη εξωτερική δύναμη είναι μόνο η βάρος,

άρα το κέντρο μάζας

διαγράφει παραβολική τροχιά

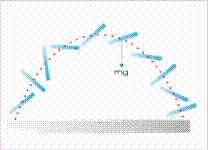
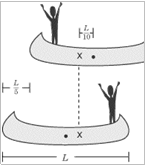Εφόσον στο σύστημα

δεν ασκούνται

εξωτερικές δυνάμεις

το αρχικά ακίνητο

κέντρο μάζας του συστήματος

παραμένει ακίνητο

Κέντρο μάζας και κίνηση

Κατά τη μεταφορική κίνηση ενός σώματος :

Η συνισταμένη των ασκουμένων εξωτερικών δυνάμεων διέρχεται από το κέντρο μάζας .

Η ολική ροπή των εξωτερικών δυνάμεων ως προς το κέντρο μάζας είναι μηδενική.

Αν σε αρχικά ακίνητο σώμα ασκηθούν δυνάμεις που συνιστούν ζεύγος το σώμα θα εκτελέσει στροφική κίνηση με το κέντρο μάζας να είναι σημείο του άξονα περιστροφής.

Κατά τη στροφική κίνηση περί άξονα που περνά από το κέντρο μάζας η ολική ροπή των εξωτερικών δυνάμεων ως προς το κέντρο μάζας είναι ίση με «το γινόμενο ροπή αδράνειας ως προς τον άξονα περιστροφής επί τη γωνιακή επιτάχυνση του σώματος».

Αν ένα σώμα εκτελεί ως προς το έδαφος χωρίς ολίσθηση, για έναν παρατηρητή κινούμενο με την ταχύτητα και την επιτάχυνση του κέντρου μάζας η κίνηση είναι στροφική περί άξονα που περνά από το κέντρο μάζας. ως προς σύστημα αναφοράς το έδαφος

Κέντρο μάζας και κινητική ενέργεια.

Η – ως σύστημα αναφοράς R - κινητική ενέργεια ενός συνόλου υλικών σημείων είναι άθροισμα των, ως προς R, κινητικών ενεργειών των υλικών αυτών σημείων.

Αποδεικνύεται ότι η τιμή της είναι ίση με ½mυ_cm²+ K_cm

όπου m η μάζα του αέρα, υ η ταχύτητα του κέντρου μάζας και K_cm το άθροισμα των κινητικών ενεργειών των υλικών σημείων ως προς το κέντρο μάζας

Εφόσον ένα σώμα εκτελεί μεταφορική κίνηση ισχύει K_cm = 0 διότι οι – ως προς το κέντρο μάζας- ταχύτητες είναι όλες μηδενικές, άρα η κινητική του ενέργεια είναι ίση με ½mυ_cm²

Κέντρο μάζας και βαρυτική δυναμική ενέργεια.

Η ( βαρυτική) δυναμική ενέργεια ενός σώματος, ως προς οριζόντια επιφάνεια ορίζεται ως άθροισμα των δυναμικών ενεργειών των υλικών σημείων του ως προς την οριζόντια επιφάνεια.

Αποδεικνύεται ότι η τιμή είναι ίση με το γινόμενο του βάρους του σώματος επί

την απόσταση h_cm του κέντρου μάζας από την οριζόντια επιφάνεια. U = mgh_cm.

Πρόκειται για την αύξηση της βαρυτικής δυναμικής ενέργειας την οποία θα παρουσιάσει το σύστημα «σώμα –Γη», εάν το σώμα είχε μετακινηθεί έτσι ώστε το κέντρο μάζας να μετατοπιστεί από οποιοδήποτε από σημείο της επιφάνειας αναφοράς στη θέση που βρίσκεται τώρα. Η σχέση ισχύει εφόσον το σώμα καταλαμβάνει περιοχή όπου το πεδίο βαρύτητας μπορεί να θεωρηθεί ομογενές.

2. Η - μέσα από τη διδασκαλία –

οικοδόμηση της έννοιας ΚΕΝΤΡΟ ΜΑΖΑΣ

Το πρώτο βήμα. Τα φαινόμενα . Πειραματική αναζήτηση του κέντρου βάρους ενός σώματος με διαδοχικές αναρτήσεις . Ομοιότητες και διαφορές ανάμεσα σε κέντρο βάρους και κέντρο μάζας

Νέες τεχνολογίες. Προβολή με κινούμενο αντικείμενο σε σχεδόν λείο έδαφος σε τυχαία κίνηση με τη συνισταμένη των ασκουμένων δυνάμεων μηδενική.

Παρατήρηση για την κίνηση του κέντρου μάζας.

Προβολή με εκτοξευμένο αντικείμενο πλάγια προς τα πάνω. Παρατήρηση για την κίνηση του κέντρου μάζας.

Το δεύτερο βήμα. Η θέση του κέντρου βάρους και του κέντρου μάζας. Προσδιορισμός της θέσης με το θεώρημα των ροπών.

Το τρίτο βήμα. Η ορμή ενός συστήματος έχει πάντα μέτρο ίσο με το γινόμενο μάζα του συστήματος επί την ταχύτητα του κέντρου μάζας. Η ορμή ενός σώματος σε στροφική κίνηση περί άξονα διερχόμενο από το κέντρο μάζας ίση με μηδέν.

Το τέταρτο βήμα. Ο δεύτερος νόμος της κίνησης με τη μορφή F_εξ = ma_cm .

Το θεώρημα του κέντρου μάζας. Ερμηνεία των φαινομένων που παρατηρήθηκαν στο πρώτο βήμα.

Οι εξισώσεις ΣF_x = 0 ΣF_y = 0 εξασφαλίζουν μηδενική επιτάχυνση στο κέντρο μάζας.

Αν οι ασκούμενες σε κινούμενο σώμα δυνάμεις είναι ομοεπίπεδες και θεωρήσουμε άξονα x στη διεύθυνση της επιτάχυνσης και άξονα y κάθετο σε αυτόν στο επίπεδο των δυνάμεων

Για ένα σώμα σε μεταφορική κίνηση . ΣF_x = ma_cm ΣF_y = 0 Στ_cm = 0

Για ένα σώμα σε κύλιση χωρίς ολίσθηση ΣF_x = ma_cm ΣF_y = 0 Στ_cm = Ι_cm α_γων

Το πέμπτο βήμα. Κέντρο μάζας και κινητική ενέργεια.

Η κινητική ενέργεια ενός συστήματος ίση με ½mυ_cm²+ K_cm

Η κινητική ενέργεια του συνόλου των σωματιδίων- μορίων που συγκροτούν ένα αέριο με ακίνητο κέντρο μάζας ίση με το άθροισμα K_cm των κινητικών ενεργειών των σωματιδίων ως προς το κέντρο μάζας.

Το έκτο βήμα . Κέντρο μάζας και βαρυτική δυναμική ενέργεια .

3. Το «όνομα του ρόδου».

Κάθε τυπική έννοια έχει ένα «δικό της» όνομα - αφηρημένο ουσιαστικό – το οποίο συνιστά το σημαίνον της

Στην πλειονότητα των ευρωπαϊκών γλωσσών ο όρος δημιουργείται από σύζευξη του όρου της φυσικής «μάζα» με ένα γεωμετρικό όρο, συνήθως τον «κέντρο», centro στα ισπανικά, center στα αγγλικά, центр στα ρώσικα, αλλά σε ορισμένες γλώσσες και τον «κεντρικό σημείο» mittelpunkt στα γερμανικά, middelpunt στα ολλανδικά, midtpunkt στα δανέζικα. Οι Γάλλοι είναι ίσως οι μόνοι που χρησιμοποιούν αντί για μάζα την έννοια αδράνεια και προτιμούν το centre d’ inertie κέντρο αδράνειας. Ενδιαφέρουσα επιλογή.

Η , σε γλώσσα ελληνική , έννοια κέντρο μάζας, στην αγγλική γλώσσα έχει το όνομα center of mass

στη γαλλική centre d’ inertie στην ιταλική centro di massa, στην ισπανική centro de masas

στην πορτογαλική centro de massa στη ρουμανική centrul de masă

στη γερμανική Massenmittelpunkt , στην ολλανδική, massamiddelpunt, στη σουηδική

στη νορβηγική massesenter στη γλώσσα των Δανών massemidtpunkt

στην πολωνική, στα τσέχικα hmotný stred και στα σλοβένικα, στα κροάτικα centar masa

στα σέρβικα ентар маса, στα βουλγάρικα Център на масите στα ρώσικα центр масс ( σέντερ μας ) στα ουκρανικά Центр мас

στην αλβανική qendra e masës, στην ουγγρική tömegközéppont, στη φιλανδική massakeskipiste, στα γλώσσα των Εσθονών massikeskme,

στη γλώσσα των Λιθουανών masės centras , στη γλώσσα των Λεττονών masės centras,

στη γλώσσα των Τούρκων kütle merkezi , στη γλώσσα των Αζέρων kütləvi mərkəzi .

4. Εννοιακό δίκτυο

Κάθε έννοια δεν υπάρχει παρά μόνο λόγω των σχέσεών της με άλλες έννοιες. Είναι όπως στο δίχτυ, όπου κάθε θηλιά δεν έχει αυτόνομη ύπαρξη. Υπάρχει λόγω των άλλων θηλιών με τις οποίες συνδέεται. Έτσι το δίχτυ συνιστά ένα σύνολο.

Το εννοιακό δίκτυο στην περιοχή της έννοιας «κέντρο μάζας».Έννοιες που ανήκουν στην περιοχή του εννοιακού δικτύου όπου βρίσκεται η κέντρο μάζας, συνδεόμενες με αυτήν με κάποιο είδος θηλιάς, είναι η κέντρο βάρους, η μάζα, η βάρος, η ορμή ενός συστήματος, η κινητική ενέργεια, η βαρυτική δυναμική ενέργεια ενός συστήματος.