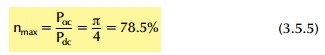3.5 Ενισχυτής τάξης B
Η μικρή απόδοση των ενισχυτών τάξης Α είναι σοβαρό πρόβλημα στα
συστήματα που έχουν μεγάλη ισχύ. Έτσι, οι μεγάλοι πομποί εκπέμπουν ισχύ αρκετών kW και, συνεπώς, αν η απόδοση ισχύος τους είναι μικρή το κόστος λειτουργίας τους θα είναι μεγάλο. Επίσης και το αρχικό κόστος κατασκευής των πομπών αυτών θα είναι μεγάλο, εφόσον χρειάζονται πιο ακριβά και υψηλής ισχύος στοιχεία κατασκευής και εξαρτήματα.
Ένα μεγάλο μέρος της ισχύος απωλειών των ενισχυτών οφείλεται στην ισχύ απωλειών στο συλλέκτη. Συνεπώς, μπορουμε να έχουμε αξιοσημείωτη βελτίωση της απόδοσης αν ελαττωθεί αυτή η ισχύς απωλειών. Επειδή η ισχύς είναι ίση με το γινόμενο του ρεύματος επί την τάση, η ισχύς απωλειών στο συλλέκτη θα είναι ανάλογη της τάσης και του ρεύματος συλλέκτη. Επομένως, αν μπορέσουμε να περιορίσουμε τη δράση του ρεύματος συλλέκτη αναγκάζοντάς το να κυκλοφορεί μόνο κατά τη διάρκεια που η τάση συλλέκτη είναι στο χαμηλότερο της κορυφής τότε θα έχουμε σημαντικό υποβιβασμό των απωλειών.
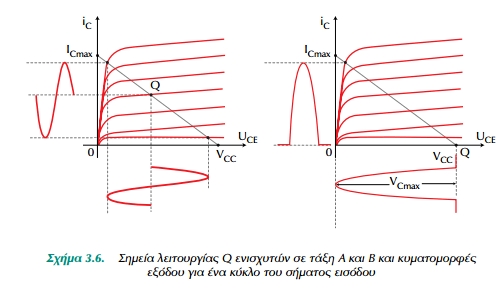
Αυτό μπορεί να γίνει πολώνοντας τον ενισχυτή σε "αποκοπή", δηλ. κάνοντας τον ενισχυτή μη αγώγιμο για μηδενικό σήμα στην είσοδο. Για ημιτονικό σήμα εισόδου το τρανζίστορ άγει μόνο κατά το μισό του σήματος εισόδου. Κατά τη διάρκεια του άλλου μισού το τρανζίστορ είναι σε αποκοπή και δεν άγει, δηλ. λειτουργεί σε τάξη Β. Το Σχ.3.6
δείχνει την κυματομορφή για λειτουργία σε τάξη Β σε σύγκριση με την τάξη Α.
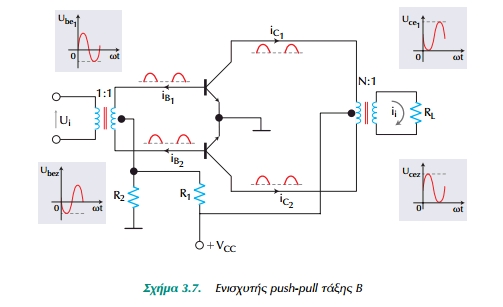
Ενώ στην τάξη Α το ρεύμα συλλέκτη κυκλοφορεί κατά τη διάρκεια ολόκληρου του κύκλου του σήματος εισόδου, στην τάξη Β το ρεύμα συλλέκτη υπάρχει και κυκλοφορεί κατά τη διάρκεια του μισού κύκλου του σήματος εισόδου. Το γεγονός αυτό οδηγεί σε ισχυρή παραμόρφωση του σήματος εξόδου. Για τις περισσότερες περιπτώσεις η παραμόρφωση αυτή δεν είναι αποδεκτή. Δύο τέτοιοι, όμως, ενισχυτές (τάξης Β) μπορούν να συνεργασθούν ώστε να δώσουν στην έξοδο κανονική κυματο- μορφή χωρίς παραμόρφωση. Το Σχ.3.7 δείχνει έναν τέτοιο ενισχυτή ο οποίος ονομάζεται ενισχυτής push-pull σε τάξη Β (με μετασχηματιστή). Η
βασική απαίτηση για τσν ενισχυτή αυτόν είναι τα δυο τρανζίστορ να
έχουν το ιδιο ρεύμα, ετσι ωστε να ενισχύονται εξίσου τα δυο μισα κάθε κύκλου των κυματομορφων.
3.5.1 Ενισχυτής Push-Pull
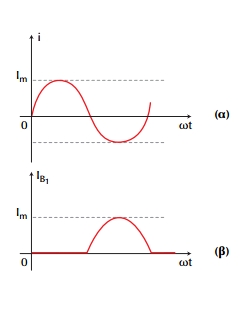
Θα γίνει τώρα μια μικρή περιγραφή της λειτουργίας του ενισχυτή push-pull, με τη βοήθεια των κυματομορφών στα διάφορα σημεία αυτού, όπως εικονίζονται το Σχ.3.8, υποθέτοντας ιδανικά στοιχεία και ιδανικές συνθήκες. Στην είσοδο του όλου ενισχυτή υποθέτουμε ένα σήμα εισόδου εκφραζόμενο απο ένα ημιτονικό ρεύμα εισόδου πλάτους I0, ήτοι στο
πρωτεύον του μετασχηματιστή εισόδου θα έχουμε ένα ρεύμα, όπως αυτό που δείχνει το σχήμα
O μετασχηματιστής εισόδου εχει λόγο σπειρών 1:1 και μεσαία λήψη (ακριβώς στο μέσο του δευτερεύοντος). Συνεπώς, θα αποστέλλει στις βάσεις των δυο τρανζίστορ, Τ1, Τ2, δυο ρεύματα ίδιου πλάτους, Im, αλλά ευρισκόμενα σε αντίθεση φάσης (δηλ. διαφορά φάσης
180°). Στο πρώτο μισό του κύκλου εναλλαγής του σήματος εισόδου, το τρανζίστορ Τ1
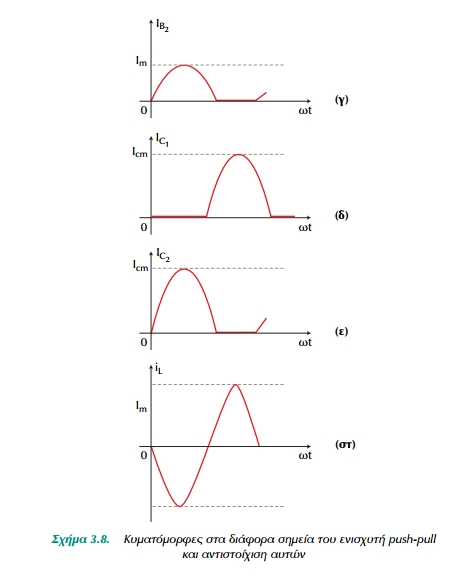
πολώνεται απο το σήμα αυτο σε κατάσταση αποκοπής, άρα δεν άγει, κι έτσι τόσο το ρεύμα βάσης του, iB1, όσο και το ρεύμα συλλέκτη του, iC1, είναι μηδενικά (Σχ.3.8 β,δ). Στο ίδιο
διάστημα, το άλλο τρανζίστορ, Τ2, άγει, πολωμένο στην ενεργό περιοχή, κι έτσι τα ρεύματα βάσης και συλλέκτη του, iB2 και iC2, , θα παρακολουθούν το σήμα εισόδου, όπως δείχνουν το Σχ.3.8 γ και ε.
Όπως φαίνεται στο Σχ.3.7 τα δύο ρεύματα IC1 και IC2 (στιγμιαίες τιμές) οδηγούνται στη μεσαία λήψη του πρωτεύοντος του μετασχηματιστή εξόδου διαρρέοντάς το με αντίθετες φορές, άρα θα επάγουν στο δευτερεύον τάσεις εξ' επαγωγής αντίθετης πολικότητας και συνεπώς ρεύματα φόρτου αντίθετης φοράς. Έτσι, αν n είναι ο λόγος σπειρών του μετασχηματιστή εξόδου, το συνιστάμενο ρεύμα στο φόρτο θα είναι
Αυτή η σχέση επαληθεύεται και από τη γραφική αφαίρεση των κυμα- τομορφών των Σχ.3.8
δ και ε, πράγμα που οδηγεί στην κυματομορφή του ρεύματος φόρτου του Σχ.3.8 στ.
Τα παραπάνω ισχύουν υπό ιδανικές προϋποθέσεις. Στην πράξη ωστόσο, στα σημεία όπου οι κυματομορφές διασταυρώνονται με τον οριζόντιο άξονα χρόνου (0, 0', 0'', ...) εμφανίζεται ισχυρή τοπική παραμόρφωση, που ονομάζεται παραμόρφωση διασταύρωσης και οφείλεται στο ότι οι χαρακτηριστικές των τρανζίστορ δεν είναι γραμμικές κοντά στο μηδέν. Για να περιοριστεί αυτή η παραμόρφωση, τα τρανζίστορ του ενισχυτή push-pull δεν πολώνονται ακριβώς σε τάξη Β αλλά ελαφρά δεξιώτερα, δηλ σε τάξη ΑΒ. Επειδή όμως, αυτή η απόκλιση είναι μικρή (περί τα 0.65 V), γι' αυτό οι ενισχυτές αυτοί θεωρούνται κατά προσέγγιση πολωμένοι σε τάξη Β.
Ισχείς σε τάξη Β
Η ισχύς (ac) εξόδου εξακολουθεί να δίνεται από την Εξ.(3.4.6) η οποία ισχύει ανεξάρτητα από την τάξη λειτουργίας. Στην περίπτωση όμως της τάξης Β, σύμφωνα με το Σχ.3.8 β, η μέγιστη δυνατή τιμή πλάτους της τάσης συλλέκτη (ac διακύμανση), θα είναι VCO = VCC. Αρα, κατά την Εξ.(3.4.6), η μέγιστη ισχύς εξόδου θα δίνεται από την έκφραση
Εξ' άλλου, αποδεικνύεται ότι, σε τάξη Β, η dc ισχύς που παρέχεται
από την πηγή τροφοδοσίας σε κάθε συλλέκτη δίνεται από τη σχέση
Pdc = 2VcCco (3.5.4)
'Αρα, η μέγιστη απόδοση ενός ενισχυτή σε τάξη Β θα είναι
Η σχέση αυτή παρέχει την απόδοση σε τάξη Β είτε για κανονικό ενι-
σχυτή ισχύος είτε για ενισχυτή ισχύος push-pull.
Τέλος, αποδεικνύεται ότι η μέγιστη τιμή της ισχύος που αποδίδεται
στο φορτίο RL δίνεται από τον τύπο
όπου R'L = N2RL η αντίσταση RL ανηγμένη (ως ανακλώμενη αντίσταση)
στο πρωτεύον του μετασχηματιστή εξόδου (βλ. Σχ.3.5 β). Με βάση τις σχέσεις αυτές μπορεί να υπολογισθεί η αντίσταση φόρτου η απαιτούμενη για δεδομένη ισχυ pUirax .
Είναι χρήσιμο να κλείσουμε αυτή την παράγραφο παραθέτοντας
συγκεντρωτικά τα πλεονεκτήματα της ενίσχυσης ισχύος σε τάξη Β,
που είναι τα εξής:
• Κατ' αρχήν, όπως φαίνεται από σύγκριση των Εξ.(3.4.5) και (3.5.5), η
λειτουργία σε τάξη Β εξασφαλίζει (μέγιστη) απόδοση ισχύος μέχρι και 78.5%, άρα κατά πολύ μεγαλύτερη από τη μέγιστη απόδοση ισχύος που επιτρέπει η τάξη Α με ωμικό φόρτο, η οποία δεν υπερβαίνει το 25%.
• Η κατανάλωση ισχύος ενός τρανζίστορ που χρησιμοποείται σε τάξη
Β είναι σημαντικά μικρότερη από όση στην τάξη Α.
• Η τάξη Β καλύπτει την ενίσχυση μεγάλων ισχυων, ενώ η τάξη Α είναι εφαρμόσιμη μόνο για τις χαμηλές και τις μέσες ισχείς.
Επιπλέον, η χρήση της τάξης Β σε συνδεσμολογία push-pull προσθέτει τα εξής πλεονεκτήματα:
α) Επειδή τα δυο ρευματα ηρεμίας-λειτουργίας στους συλλέκτες των τρανζίστορ
κυκλοφορουν με αντίθετες διευθυνσεις ροής, αναιρουνται μεταξυ τους κι έστι στο μετασχηματιστή εξόδου δεν κυκλοφορεί στον πυρήνα του μαγνητικό ρευμα κόρου, άρα βελτιώνονται οι επιδόσεις του.
β) Στο ac ρευμα εξόδου δεν υπάρχουν συνιστώσες λόγω 2ης αρμονικής, γιατί οι
συνιστώσες αυτές έχουν αντίθετες διευθυνσεις ροής και έτσι τα αντίστοιχα ρευματα αλληλο-εξουδετερώνονται.
γ) Τα ρευματα ηρεμίας βάσης και συλλέκτη και στα δυο τρανζίστορ είναι μικρά.
Παράδειγμα 3-3
O ενισχυτής push-pull του Σχ.3.7 χρησιμοποιεί τάση τροφοδοσίας 15 V και μετασχηματιστή εξόδου με πρωτευον 100 σπειρών και δευτερευον 20 σπειρών. Πόση είναι η μέγιστη τιμή της ισχυος που αποδίδεται στο φόρτο, αν αυτός είναι μεγάφωνο 8 Ω και πόσο πλάτος ac
ρεύματος πρέπει
66
ΑΝΑΛΟΓΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ
να υπάρχει στο συλλέκτη κάθε τρανζίστορ για να λαμβάνεται η παραπάνω ισχύς ως (μέγιστη) ισχύς εξόδου.
3.6 Παραμορφώσεις
Όπως είδαμε, με το πέρασμα από την τάξη Α στη Β, οι ενισχυτές ισχύος ανεβάζουν την απόδοσή τους. Αυτό όμως, αν δεν πάρουμε τα κατάλληλα μέτρα, γίνεται με θυσία της
μορφής του σήματος. Έτσι το θέμα των παραμορφώσεων αποκτά μεγάλη σημασία.
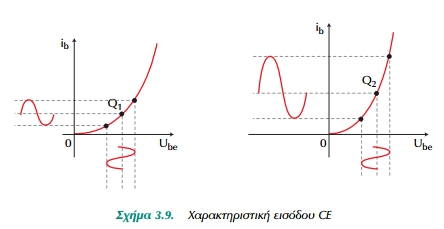
Οι παραμορφώσεις στους ενισχυτές οφείλονται στη μη γραμμικότητα των χαρακτηριστικών εισόδου και εξόδου. Το Σχ.3.9 δείχνει τη χαρακτηριστική εισόδου ενός τρανζίστορ σε συνδεσμολογία CE. Όπως βλέπουμε η χαρακτηριστική είναι ιδιαίτερα καμπυλόγραμμη στο κάτω μέρος της.
Όταν λοιπόν στην είσοδο εφαρμοστεί σήμα vbe = V sin ωί, η κυματομορφή ρεύματος που προκύπτει είναι περισσότερο συμπιεσμένη προς την αρνητική (κάτω) κορυφή, Σχ.3-9 α,
παρά όταν το σημείο πόλωσης βρίσκεται σε υψηλότερο σημείο (Q2), Σχ.3.9 β. Επίσης, στο χαμηλότερο σημείο πόλωσης επειδή το σήμα είναι μικρότερο.
ΕΝΙΣΧΥΤΕΣ ΙΣΧΥΟΣ
67
Όταν ένα ημιτονικό σήμα παραμορφωθεί, αποδεικνύεται μαθηματικά, (με ανάλυση κατά Fourier), ότι δημιουργούνται επιπρόσθετα ημιτονικά σήματα. Οι συχνότητες των ημιτονικων αυτών σημάτων "παραμόρφωσης", είναι ακέραια πολλαπλάσια του αρχικού σήματος. Δηλ., αν f είναι η αρχική συχνότητα, δημιουργούνται επιπλέον οι συχνότητες 2f, 3f, 4f, κτλ. Η αρχική συχνότητα ονομάζεται βασική ή θεμελιώδης συχνότητα, ενώ οι πολλαπλάσιές της συχνότητες, ονομάζονται αρμονικές. Ειδικότερα, η 2f ονομάζεται δεύτερη αρμονική, η 3f τρίτη αρμονική, κ.ο.κ.
Οι διάφορες αρμονικές συνιστώσες που περιέχονται σ' ένα σήμα μπορούν να εντοπισθούν και να μετρηθούν χρησιμοποιώντας συντονισμένα φίλτρα στενής ζώνης. Το φίλτρο συντονίζει σε μια δεδομένη αρμονική και το σήμα εξόδου του έχει την ίδια συχνότητα. Αν η ενίσχυση του φίλτρου είναι μονάδα, το πλάτος της εξόδου του αποτελεί το πλάτος της δεδομένης αρμονικής.
Υπάρχουν εμπορικές συσκευές (φασματικοί αναλυτές) που χρησιμοποιούν την τεχνική αυτή για να μετρούν την παραμόρφωση. Στις περισσότερες περιπτώσεις οι μικρότερες σε συχνότητα αρμονικές έχουν μεγαλύτερο πλάτος, με αποτέλεσμα η μέτρηση και η ανάλυση της παραμόρφωσης να επικεντρώνεται μόνο στη 2 η και 3 η αρμονική.
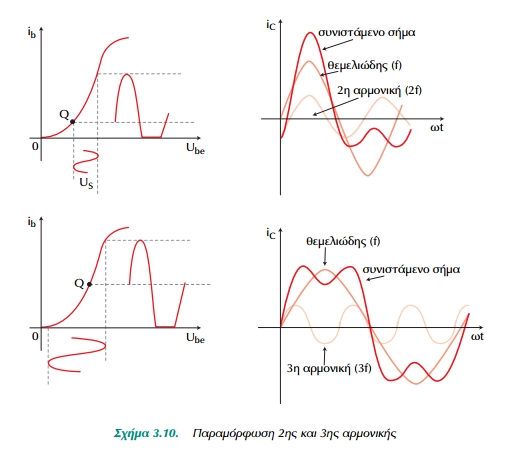
Το Σχ.3.10 δείχνει ένα ημιτονικό σήμα vs που εφαρμόζεται, κατά σειρά, σε δυο κυκλώματα που έχουν μη γραμμικές χαρακτηριστικές ή καμπύλες μεταφοράς. Το ρεύμα εξόδου σε κάθε περίπτωση μπορεί να σχεδιαστεί γραφικά για δεδομένη καμπύλη μεταφοράς. Στο Σχ.3.10
α το σημείο λειτουργίας Q και το πλάτος του σήματος είναι τέτοια ώστε το
68
ΑΝΑΛΟΓΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ
σήμα να απασχολεί μόνο το κάτω τμήμα της χαρακτηριστικής καμπύλης. Αποτέλεσμα είναι ότι το σήμα συμπιέζεται στο κάτω μέρος του. Αν όμως συμπεριλαμβάνονται και τα δύο (άνω και κάτω) καμπύλα τμήματα της χαρακτηριστικής, το σήμα συμπιέζεται και στις δυο κορυφές του.
Στο ίδιο σχήμα εικονίζονται και τα σήματα εξόδου. Στην πρώτη περίπτωση υπάρχει έντονα η 2η αρμονική συνιστώσα με αποτέλεσμα το σήμα εξοδου να έχει τη μορφή του συνιστάμενου σήματος που δείχνει το σχήμα. Η αντίστοιχη παραμόρφωση ονομάζεται παραμόρφωση άρτιας αρμονικής. Στη 2 η περίπτωση στην έξοδο εμφανίζεται με μεγάλο πλάτος η 3η αρμονική με αποτέλεσμα το συνιστάμενο σήμα να έχει τη μορφή που δείχνει το σχήμα. Αυτό το σχήμα παραμόρφωσης ονομάζεται παραμόρφωση περιττής αρμονικής.
ΕΝΙΣΧΥΤΕΣ ΙΣΧΥΟΣ
69
3.7 Παραμοφωση στους ενισχυτές push-pull
Όταν πολώνεται σε τάξη Α, ο ενισχυτής push-pull έχει το ιδίωμα ότι
τείνει να εξουδετερώσει την παραμόρφωση των περιττών αρμονικών.
Αυτό οφείλεται στο ότι τα δύο τρανζίστορ λειτουργούν με διαφορά
φάσης 180°, ώστε όταν στο ένα τρανζίστορ το σήμα είναι στη μέγιστη θετική του τιμή στο άλλο είναι στη μέγιστη αρνητική του. Το Σχ.3.11 δείχνει μόνο τη δεύτερη αρμονική. Αφού το iC2 αφαιρείται από το iC1, όπως είδαμε ότι συμβαίνει στην έξοδο του push-pull, οι αρμονικές που φαίνονται στο σχήμα αλληλο-εξουδετερώνονται, ενώ οι θεμελιώδεις συνιστώσες (που έχουν βασική συχνότητα) προστίθενται.
H εξουδετερωση αυτή γίνεται μονο για τις άρτιες αρμονικές, οχι ομως και για τις περιττές αρμονικές. Το Σχ.3.12 δείχνει, γιατί δεν εξουδετερώνονται οι περιττές αρμονικές, οι οποίες είναι προσθετικές μεταξύ τους όπως και οι θεμελιώδεις συνιστώσες.
70
ΑΝΑΛΟΓΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ
Η εξουδετέρωση των άρτιων αρμονικών αποτελεί σημαντικό πλεονέκτημα των ενισχυτών push-pull τάξης Α σε σύγκριση με τους ενισχυτές ενός τρανζίστορ. Η βελτίωση όμως αυτή επιτυγχάνεται ολοκληρωτικά, μόνο αν τα δυο τρανζίστορ του push-pull έχουν τις ίδιες χαρακτηριστικές. Αν οι χαρακτηριστικές τους δεν είναι ακριβώς ίδιες, η εξουδετέρωση δεν είναι πλήρης και απομένει κάποια παραμόρφωση στην έξοδο.
του push-pull
Όταν οι ενισχυτές push-pull λειτουργούν σε τάξη Β δε θα πρέπει να λησμονούμε την ύπαρξη της παραμόρφωσης διασταύρωσης που αναπτύξαμε ήδη στην ενότητα 3.5.