5.3 Διαμορφωτές
Διαμορφωτής (modulator) είναι η διάταξη (το κύκλωμα) με την οποία υλοποιείται η διαδικασία μιας συγκεκριμένης διαμόρφωσης.
5.3.1 Διαμορφωτές πλάτους ΑΜ με φέρον
Τα χρησιμοποιούμενα στην πράξη κυκλώματα διαμόρφωσης ΑΜ είναι πολλά. Μπορούμε να τα κατατάξουμε σε δύο κατηγορίες:
· Κυκλώματα γραμμικά, που ουσιαστικά υλοποιούν τη διαδικασία της διαμόρφωσης ακριβώς όπως τη γνωρίσαμε στο τρίτο κεφάλαιο.
· Κυκλώματα μη γραμμικά. Εδώ η διαμόρφωση επιτυγχάνεται από την παραμόρφωση που εισάγει μια δίοδος ή ένα τρανζίστορ που εργάζεται σε τάξη C (διακοπτόμενο κύκλωμα), όταν διαρρέεται από ρεύμα.
A) Κυκλώματα γραμμικά
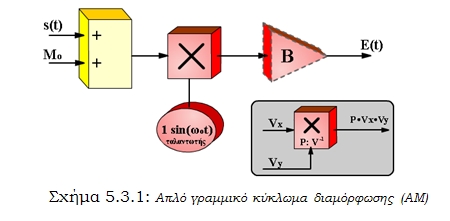
Το απλούστερο κύκλωμα διαμόρφωσης είναι αυτό του σχήματος 5.3.1.
Εύκολα επιβεβαιώνουμε ότι:
E(t) = [Mo + s(t)]. sin(ωοt) (4)
Ο πολλαπλασιαστής δίνει στην έξοδο πάντοτε ως αποτέλεσμα το γινόμενο των τάσεων στις δύο εισόδους, δηλαδή:
Vεξ = p .Vx .Vy
Ο συντελεστής πολλαπλασιασμού p μετριέται σε V-1 και χαρακτηρίζει τον πολλαπλασιαστή. Στο σχήμα θεωρήσαμε p=1 V-1.
Σήμερα υπάρχουν ολοκληρωμένα κυκλώματα που λειτουργούν έως μερικά MHz και υλοποιούν απ’ ευθείας τη διαδικασία του σχήματος 5.3.1 (παράδειγμα το MC 1495 , MC 1496 της Motorola κ.α.). Μια ειδική περίπτωση πολλαπλασιαστή είναι ο ισοσταθμισμένος διαμορφωτής δακτυλίου, που εξετάζεται σε επόμενη παράγραφο.
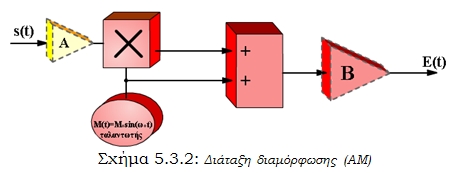
Παραλλαγή της προηγούμενης διάταξης είναι η διάταξη του σχήματος 5.3.2. Εύκολα επαληθεύεται ότι έχουμε διαμόρφωση ΑΜ.
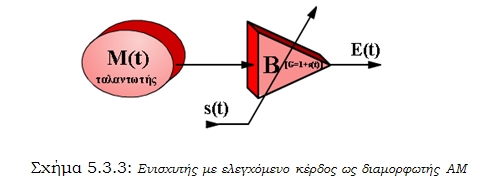
Ένα τρίτο κύκλωμα γραμμικού διαμορφωτή ΑΜ δίνεται στο σχήμα 5.3.3. Εδώ το κέρδος του ενισχυτή είναι μεταβλητό και ελέγχεται από το σήμα διαμόρφωσης s(t).
Σχήμα 5.3.3: Ενισχυτής με ελεγχόμενο κέρδος ως διαμορφωτής ΑΜ
Αν υποθέσουμε ότι το κέρδος του ενισχυτή δίνεται από την σχέση
G = 1 + s(t) (5)
στην έξοδο έχουμε το φέρον διαμορφωμένο κατά πλάτος.
B) Μη γραμμικοί διαμορφωτές ΑΜ
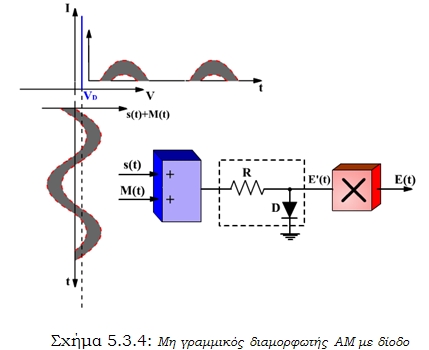
Στο σχήμα 5.3.4 αποδίδεται ένας διαμορφωτής πλάτους με δίοδο, που λειτουργεί με διακοπτόμενο ρεύμα.
Στην δίοδο εφαρμόζεται το άθροισμα του βασικού σηματος και του φέροντος που προέρχεται από τον ταλαντωτή:
V(t) = s(t) + M(t)
Το περιοδικό διακοπτόμενο ρεύμα που προκαλείται στη δίοδο έχει πλούσιο φασματικό περιεχόμενο, που μπορούμε να το προσδιορίσουμε μαθηματικά (ανάλυση Fourier). Αποδεικνύεται ότι σ αυτό το φασματικό περιεχόμενο υπάρχουν οι συμμετρικές φασματικές ακτίνες που συναντούμε στη διαμόρφωση ΑΜ (δηλαδή fo , fo + F και fo– F). Αν με κατάλληλο φίλτρο επιλέξουμε το συγκεκριμένο τμήμα του φάσματος, στην έξοδο θα πάρουμε το διαμορφωμένο φέρον, όπως σημειώνεται στο σχήμα.
Το κύκλωμα αυτό χαρακτηρίζεται από την απλότητά του και την ευκολία κατασκευής. Η τεχνολογία σήμερα κατασκευάζει διόδους που εργάζονται σε πολύ υψηλές συχνότητες (δίοδοι Sottkey) και τις χρησιμοποιούμε, για να φτιάξουμε διαμορφωτές πλάτους σε ζώνες συχνοτήτων όπου τα γραμμικά κυκλώματα που μελετήθηκαν δεν μπορούν να εργαστούν.
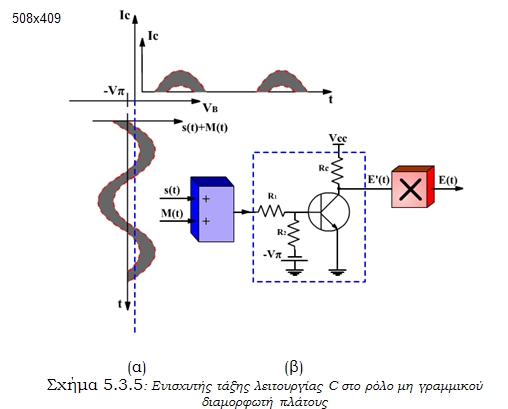
Περίπου στη φιλοσοφία του προηγούμενου κυκλώματος στηρίζεται και το επόμενο κύκλωμα, του σχήματος 5.3.5.
Πρόκειται για ενισχυτή υψηλών συχνοτήτων σε τάξη λειτουργίας C.
Στους ενισχυτές τάξης C το τρανζίστορ είναι πολωμένο αρνητικά και άγει μόνο στις θετικές κορυφές του σήματος εισόδου (σχήμα 5.3.5α).
Το πλεονέκτημα ενός τέτοιου ενισχυτή, όπως γνωρίζουμε από τα μαθήματα της ηλεκτρονικής, είναι η μεγάλη απόδοση ισχύος (η = Ρεξ / Ρτροφ ) που έχει και φτάνει έως και 80 %.
Η απόκριση του κυκλώματος εξαρτάται από την τάση τροφοδοσίας του Vcc. Στην περίπτωση που σε σειρά με την τάση τροφοδοσίας ενός τέτοιου ενισχυτή προστεθεί μέσω μετασχηματιστή το σήμα διαμόρφωσης s(t), η απόκριση του κυκλώματος ελέγχεται από το s(t) και αποδίδεται στο σχήμα 5.3.5β. Το φίλτρο εξόδου L-C αποκαθιστά πλήρως την ημιτονική κυματομορφή του φέροντος που είναι διαμορφωμένο κατά πλάτος.
Η αξιοποίηση αυτού του κυκλώματος συνδυάζει τη διαμόρφωση με το τελικό στάδιο ενίσχυσης και χρησιμοποιείται συχνά. Πρέπει να σημειώσουμε με έμφαση ότι, αν μετά τη διαμόρφωση του φέροντος κατά πλάτος ακολουθήσει στάδιο ενίσχυσης του διαμορφωμένου σήματος, πρέπει να είναι γραμμικός ενισχυτής τάξης Α, που δεν εισάγει παραμορφώσεις πλάτους (διότι θα επηρέαζαν την πληροφορία) και σέβεται πλήρως το φάσμα του διαμορφωμένου φέροντος.