- ΣΥΣΤΗΜΑΤΑ ΑΚΤΙΝΟΒΟΛΙΑΣ
Για να πραγματοποιηθούν οι ασύρματες επικοινωνίες που περιγράφηκαν στα προηγούμενα κεφάλαια, πρέπει η ισχύς εξόδου του πομπού να μεταφερθεί σε κάποια κατάλληλη διάταξη, από την οποία θα ακτινοβοληθεί στο χώρο σαν ηλεκτρομαγνητικό κύμα. Ταυτόχρονα, μια παρόμοια διάταξη θα πρέπει να συλλάβει αυτό το ηλεκτρομαγνητικό κύμα και να το μεταφέρει με μορφή ηλεκτρικού σήματος στην είσοδο ενός δέκτη όπου θα υποστεί την κατάλληλη επεξεργασία, για να μετατραπεί σε ωφέλιμο σήμα.
Οι διατάξεις που ακτινοβολούν ηλεκτρομαγνητικά κύματα στο χώρο ή συλλαμβάνουν ηλεκτρομαγνητικά κύματα από το χώρο ονομάζονται κεραίες. Οι διατάξεις που χρησιμοποιούνται για τη μεταφορά ηλεκτρικής ισχύος από τους πομπούς στις κεραίες ή από τις κεραίες στους δέκτες ονομάζονται γραμμές μεταφοράς. Στο κεφάλαιο που ακολουθεί θα περιγράψουμε τα βασικά στοιχεία αυτών των διατάξεων.
6.1 Γραμμές μεταφοράς
Όπως είδαμε στο κεφάλαιο 4, οι γραμμές μεταφοράς είναι συστήματα αγωγών που μεταφέρουν ηλεκτρομαγνητική ενέργεια μεταξύ των κεραιών και των πομπών ή των δεκτών στους οποίους αυτές συνδέονται. Γνωρίσαμε δύο τύπους γραμμών μεταφοράς, τη συμμετρική και την ασύμμετρη ή ομοαξονική. Δεχτήκαμε ότι κάθε γραμμή μπορεί να θεωρηθεί ότι αποτελείται από πλήθος πυκνωτές, πηνία και αντιστάσεις κατανεμημένα σε όλο της το μήκος. Η δράση των αντιστάσεων έχει αποτέλεσμα την απώλεια ενός μέρους της μεταφερόμενης ενέργειας, ενώ η δράση των υπόλοιπων στοιχείων περιορίζει τη μέγιστη συχνότητα του ρεύματος που μπορεί να περάσει μέσα από τη γραμμή. Τα κατανεμημένα στοιχεία καθορίζουν επίσης και τη χαρακτηριστική αντίσταση της γραμμής. Αυτή η αντίσταση, όπως είδαμε, εξαρτάται από τα κατασκευαστικά χαρακτηριστικά της γραμμής και θα ήταν η αντίσταση που θα προέβαλλε η γραμμή στη διέλευση του υψίσυχνου ρεύματος, αν είχε άπειρο μήκος.
6.1.1 Τρέχοντα κύματα
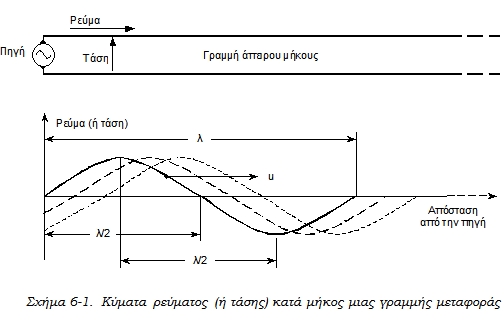
Ας υποθέσουμε ότι έχουμε μια γραμμή άπειρου μήκους, η οποία τροφοδοτείται στο ένα άκρο της από μια πηγή εναλλασσόμενης ημιτονικής τάσης υψηλής συχνότητας. Όπως είδαμε στο κεφάλαιο 4, το ρεύμα και η τάση έχουν σε μια ορισμένη στιγμή διαφορετικές τιμές από θέση σε θέση πάνω στη γραμμή. Αν με κάποιο καταγραφικό όργανο μπορούσαμε να εξετάσουμε τις τιμές του ρεύματος εκείνη τη στιγμή (τα ίδια ισχύουν και για τις τιμές της τάσης), θα βλέπαμε ότι το ρεύμα έχει κατανομή πάνω στη γραμμή όμοια με την έντονα σχεδιασμένη ημιτονική καμπύλη στο
σχήμα 6-1.
Σε επόμενες χρονικές στιγμές η ίδια καμπύλη θα μετατοπιστεί μακρύτερα από την πηγή και οι κατανομές του ρεύματος θα αντιστοιχούν στις διακεκομμένες καμπύλες. Παρατηρούμε ότι σε μια ορισμένη στιγμή το ρεύμα κατανέμεται ημιτονικά πάνω στη γραμμή. Επίσης, σε μια ορισμένη θέση της γραμμής το ρεύμα που περνάει από εκεί μεταβάλλεται ημιτονικά με την πάροδο του χρόνου. Μια τέτοια μεταβολή στο χώρο και το χρόνο ονομάζεται κύμα. Επειδή το ρεύμα και η τάση σχηματίζουν κύματα που μετακινούνται πάνω στη γραμμή, τα ονομάζουμε τρέχοντα κύματα.
Η ταχύτητα u με την οποία μετακινούνται τα τρέχοντα κύματα πάνω στη γραμμή εξαρτάται από το είδος του μονωτικού υλικού μεταξύ των συρμάτων. Αν στη θέση του μονωτικού υπάρχει το κενό, η ταχύτητα είναι ίση με την ταχύτητα του φωτός (300.000 km/sec). Σε κάθε άλλη περίπτωση η ταχύτητα είναι από 5 ως 20% μικρότερη.
Εκτός από την ταχύτητα διάδοσης, ένα κύμα έχει και ορισμένο μήκος κύματος λ. Το μήκος κύματος είναι η απόσταση μεταξύ δύο όμοιων μηδενισμών ή μεταξύ δύο διαδοχικών μεγίστων της τιμής του ρεύματος ή της τάσης. Το μήκος κύματος συνδέεται με την ταχύτητα u του κύματος και τη συχνότητα f του ρεύματος της πηγής, σύμφωνα με τη σχέση:
λ=u/f (6.1)
Όλα τα παραπάνω ισχύουν για μια γραμμή που έχει άπειρο μήκος και καθόλου απώλειες. Όταν η γραμμή δεν έχει άπειρο μήκος, τα πράγματα αλλάζουν σημαντικά, εκτός και αν στο άλλο άκρο της γραμμής συνδέεται μια αντίσταση φορτίου καθαρά ωμική και ίση με τη χαρακτηριστική αντίσταση της γραμμής. Τότε η τάση και το ρεύμα συμπεριφέρονται με τον τρόπο που περιγράψαμε παραπάνω και η γραμμή λειτουργεί σαν να έχει άπειρο μήκος.
6.1.2 Στάσιμα κύματα
Ας υποθέσουμε τώρα ότι έχουμε μια γραμμή μεταφοράς που δεν έχει άπειρο μήκος και στο τέρμα της δε συνδέεται αντίσταση φορτίου. Όταν μια τέτοια γραμμή συνδεθεί σε μια πηγή που παράγει εναλλασσόμενη τάση με πλάτος V, κατά τη στιγμή της σύνδεσης η πηγή "αισθάνεται" στα άκρα της μια αντίσταση ίση με τη χαρακτηριστική αντίσταση Rc της γραμμής. Αρχίζει λοιπόν να κινεί ένα ρεύμα με πλάτος Ιπρ, που υπολογίζεται από τη σχέση: Ιπρ = V/Rc.
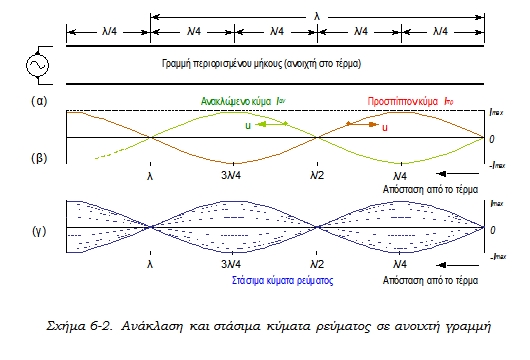
Το ρεύμα αυτό προχωρεί σαν κύμα προς το τέρμα της γραμμής με ταχύτητα διάδοσης u, χωρίς αρχικά να "γνωρίζει" τι φορτίο θα συναντήσει εκεί. Το κύμα αυτό ονομάζεται προσπίπτον κύμα ρεύματος και, παρ' όλο που η ταχύτητα u είναι πολύ μεγάλη, το κύμα φτάνει στο φορτίο μετά από κάποιο μικρό χρονικό διάστημα, που ονομάζεται χρόνος καθυστέρησης. Ο χρόνος καθυστέρησης προκαλεί αλλαγή στη φάση του ρεύματος. Τα ίδια συμβαίνουν και στο κύμα τάσης, που διαδίδεται ταυτόχρονα με το ρεύμα. Όταν το προσπίπτον κύμα ρεύματος φτάσει στο τέρμα της γραμμής, συναντά μια άπειρη αντίσταση, αφού εκεί δεν υπάρχει συνδεδεμένο κανένα φορτίο. Μέσα από άπειρη αντίσταση δεν μπορεί να κυκλοφορήσει ρεύμα. Στο τέρμα της γραμμής λοιπόν η τιμή του ρεύματος είναι μηδέν και το προσπίπτον κύμα αναγκάζεται να επιστρέψει πίσω στην πηγή. Το κύμα που επιστρέφει ονομάζεται ανακλώμενο κύμα και έχει πλάτος Ιαν ίσο με το πλάτος του προσπίπτοντος κύματος. Τα δύο κύματα συνδυάζονται, με αποτέλεσμα να έχουμε σε άλλα σημεία αύξηση και σε άλλα σημεία εξασθένηση του συνολικού πλάτους.
Όταν το ανακλώμενο κύμα φτάσει στην πηγή, η κατάσταση αυτή παγιώνεται. Τότε έχουμε ταυτόχρονη μεταβολή του ρεύματος (και της τάσης) με διάφορα πλάτη στα διάφορα σημεία της γραμμής, όπως φαίνεται στο σχήμα 6-2(γ), αλλά καμιά κίνηση κύματος δεν παρατηρείται. Η κατάσταση αυτή ονομάζεται στάσιμο κύμα. Τα σημεία όπου το πλάτος της κύμανσης είναι μέγιστο ονομάζονται κοιλίες, ενώ τα σημεία όπου το πλάτος είναι μηδενικό ονομάζονται δεσμοί. Οι κατανομές πλάτους επαναλαμβάνονται κατά διαστήματα ίσα με λ/2. Αυτό αποτελεί γενική ιδιότητα των γραμμών μεταφοράς.
Όπως υπάρχουν στάσιμα κύματα ρεύματος, έτσι υπάρχουν και στάσιμα κύματα τάσης. Η διαφορά μεταξύ τους είναι ότι στο ανοιχτό τέρμα της γραμμής εκδηλώνεται πάντοτε κοιλία τάσης. Αυτό είναι αναμενόμενο, αφού είναι γνωστό ότι σε οποιοδήποτε ανοιχτό κύκλωμα η τάση στα άκρα του είναι ίση με την τάση στους πόλους της πηγής. Έτσι, υπάρχει διαφορά φάσης ίση με λ/4 ή 90ο μεταξύ των στάσιμων κυμάτων ρεύματος και τάσης σε μια ανοιχτή γραμμή.
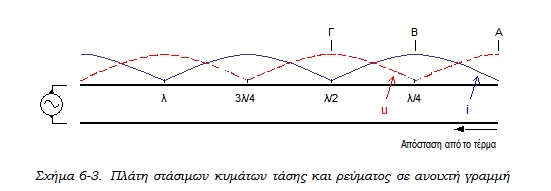
Στο σχήμα 6-3 φαίνονται τα πλάτη (και όχι οι στιγμιαίες τιμές) των στάσιμων κυμάτων ρεύματος και τάσης κατά μήκος μιας ανοιχτής γραμμής. Συγκρίνετε αυτό το σχήμα με το σχήμα 6-2(γ), για να κατανοήσετε τη διαφορά στην απεικόνιση.
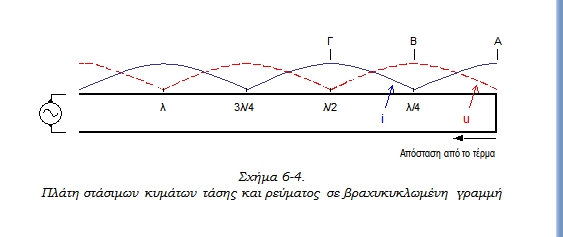
Ανάλογα φαινόμενα ισχύουν και όταν η γραμμή δεν είναι ανοιχτή στο τέρμα της, αλλά βραχυκυκλωμένη. Λόγω του βραχυκυκλώματος, στο τέρμα της γραμμής η τάση είναι πάντα μηδέν και το ρεύμα μέγιστο. Με μηδενική τάση όμως η ενέργεια που δίνει η πηγή στη γραμμή δεν μπορεί να καταναλωθεί και έτσι πρέπει να επιστρέψει πίσω. Αναπτύσσονται λοιπόν και πάλι στάσιμα κύματα ρεύματος και τάσης κατά μήκος της γραμμής, που όμως εμφανίζουν κοιλία ρεύματος και δεσμό τάσης στο τέρμα. Η μορφή αυτών των στάσιμων κυμάτων φαίνεται στο σχήμα 6-4. Παρατηρήστε ότι υπάρχει και πάλι η διαφορά φάσης των 90ο μεταξύ της τάσης και του ρεύματος.
6.1.3 Συντονισμένες γραμμές
Ας παρατηρήσουμε και πάλι το σχήμα 6-3. Στη θέση Β, που απέχει απόσταση λ/4 από το ανοιχτό τέρμα της γραμμής, το πλάτος της τάσης (διακεκομμένη γραμμή) είναι μηδέν, ενώ το πλάτος του ρεύματος (συνεχής γραμμή) είναι μέγιστο. Η αντίσταση σ' αυτό το σημείο, που ως γνωστόν προκύπτει από τη σχέση R=U/I, είναι μηδέν. Αν η πηγή ήταν συνδεδεμένη στη θέση Β, θα αντιμετώπιζε βραχυκύκλωμα στα άκρα της, άσχετα με το γεγονός ότι η γραμμή είναι ανοιχτή. Αυτό βέβαια συμβαίνει σε μια ιδανική γραμμή, που δεν έχει απώλειες. Σε πραγματική γραμμή η αντίσταση στη θέση Β είναι πολύ μικρή, αλλά όχι μηδενική. Αντίθετα στο σημείο Γ, που απέχει απόσταση λ/2 από το τέρμα της γραμμής, το πλάτος της τάσης είναι μέγιστο, ενώ το πλάτος του ρεύματος είναι μηδέν. Η αντίσταση σ' αυτό το σημείο προκύπτει ότι είναι άπειρη (ή πάρα πολύ μεγάλη, αν η γραμμή είναι πραγματική).
Μεταξύ του σημείου Β και του Α η αντίσταση αυξάνει όσο η απόσταση από το τέρμα μικραίνει. Επειδή στο τμήμα αυτό το ρεύμα προηγείται της τάσης κατά 90ο, η γραμμή συμπεριφέρεται σαν πυκνωτής, με χωρητικότητα που μικραίνει όσο το μήκος της μικραίνει. Μεταξύ του σημείου Β και του Γ η αντίσταση και πάλι αυξάνει όσο η απόσταση από το τέρμα μεγαλώνει. Επειδή όμως στο τμήμα αυτό η τάση προηγείται του ρεύματος κατά 90ο, η γραμμή συμπεριφέρεται σαν πηνίο, με αυτεπαγωγή που μεγαλώνει όσο το μήκος της μεγαλώνει.
Όλα αυτά θυμίζουν το φαινόμενο του συντονισμού σε κυκλώματα με πηνίο και πυκνωτή. Σε ανοιχτή γραμμή, όταν το μήκος είναι λ/4 (ή περιττό, δηλαδή μονό πολλαπλάσιο του λ/4), η αντίσταση είναι ελάχιστη και η γραμμή συμπεριφέρεται σαν κύκλωμα LC σειράς σε συντονισμό. Όταν το μήκος είναι λ/2 (ή πολλαπλάσιο του λ/2), η αντίσταση είναι μέγιστη και η γραμμή συμπεριφέρεται σαν κύκλωμα LC παραλληλίας σε συντονισμό. Με μήκος μεταξύ λ/4 και 0, η ανοιχτή γραμμή συμπεριφέρεται σαν πυκνωτής, ενώ με μήκος μεταξύ λ/4 και λ/2, συμπεριφέρεται σαν πηνίο (σχήμα 6-5). Αυτό μας επιτρέπει να χρησιμοποιήσουμε ένα κομμάτι τέτοιας γραμμής σε ρόλο ενός πυκνωτή ή ενός πηνίου, του οποίου η χωρητικότητα ή η αυτεπαγωγή ρυθμίζονται, μεταβάλλοντας κατάλληλα το μήκος της γραμμής. Αυτό το κάνουμε συχνά στις πολύ υψηλές συχνότητες όπου οι συνηθισμένοι πυκνωτές και τα πηνία δε λειτουργούν ικανοποιητικά.
Ανάλογα φαινόμενα ισχύουν και για την περίπτωση που η γραμμή είναι βραχυκυκλωμένη στο τέρμα της. Μόνο που τώρα τα πράγματα είναι αντίθετα απ' ό,τι προηγουμένως, επειδή, όπως μπορούμε να δούμε στο σχήμα 6-4, στο τέρμα της γραμμής η τάση είναι μηδέν και το ρεύμα μέγιστο. Έτσι, μια βραχυκυκλωμένη γραμμή με μήκος λ/4 ή περιττό πολλαπλάσιο του λ/4 παρουσιάζει άπειρη (πάρα πολύ μεγάλη) αντίσταση εισόδου και συμπεριφέρεται σαν κύκλωμα LC παραλληλίας σε συντονισμό. Όταν το μήκος της είναι λ/2 ή πολλαπλάσιο του λ/2 τότε η αντίσταση εισόδου της είναι μηδενική (πολύ μικρή) και η γραμμή συμπεριφέρεται σαν κύκλωμα LC σειράς σε συντονισμό. Όταν έχει μήκος μικρότερο του λ/4, η βραχυκυκλωμένη γραμμή συμπεριφέρεται σαν πηνίο με αυτεπαγωγή, που μικραίνει όσο μικραίνει το μήκος της, ενώ, όταν έχει μήκος μεταξύ λ/4 και λ/2, συμπεριφέρεται σαν πυκνωτής, του οποίου η χωρητικότητα μεγαλώνει όσο μεγαλώνει το μήκος (σχήμα 6-6).
Όλα τα παραπάνω μπορούν να συμβούν είτε όταν κρατάμε σταθερή τη συχνότητα της πηγής και μεταβάλλουμε το μήκος της γραμμής είτε όταν κρατάμε σταθερό το μήκος της γραμμής και μεταβάλλουμε τη συχνότητα. Πράγματι, όπως είδαμε στην αρχή (σχέση 6.1), το μήκος κύματος λ εξαρτάται από τη συχνότητα f της πηγής. Μεταβάλλοντας τη συχνότητα, ένα δοσμένο μήκος γραμμής μπορεί να αντιστοιχεί σε τμήμα λ/4 ή λ/2 ή οποιοδήποτε άλλο κλάσμα ή και πολλαπλάσιο του λ. Με τη μεταβολή της συχνότητας η αντίσταση εισόδου της γραμμής αλλάζει και, όταν η συχνότητα γίνει τέτοια, ώστε το κομμάτι της γραμμής να αντιστοιχεί ακριβώς σε τμήμα λ/4, έχουμε συντονισμό.
Ανοικτά ή βραχυκυκλωμένα τμήματα γραμμών με μήκος λ/4 χρησιμοποιούνται πολύ συχνά σαν συντονισμένα κυκλώματα στις πολύ υψηλές συχνότητες. Η συμπεριφορά τους είναι πολύ καλύτερη από τη συμπεριφορά των συνηθισμένων κυκλωμάτων LC και συχνά αποτελούν το μόνο τρόπο να κατασκευαστεί κύκλωμα συντονισμού, γιατί, όπως είπαμε, στις πολύ υψηλές συχνότητες δεν είναι εύκολη η κατασκευή κατάλληλων πηνίων και πυκνωτών.
6.1.4 Γραμμές με ωμικό φορτίο
Ας εξετάσουμε τώρα την περίπτωση μιας γραμμής, στο τέρμα της οποίας είναι συνδεδεμένο ένα ωμικό φορτίο. Όπως είπαμε, όταν το φορτίο έχει τιμή ίση με τη χαρακτηριστική αντίσταση της γραμμής, η γραμμή συμπεριφέρεται σαν να είχε άπειρο μήκος και από μέσα της περνούν μόνο τρέχοντα κύματα.
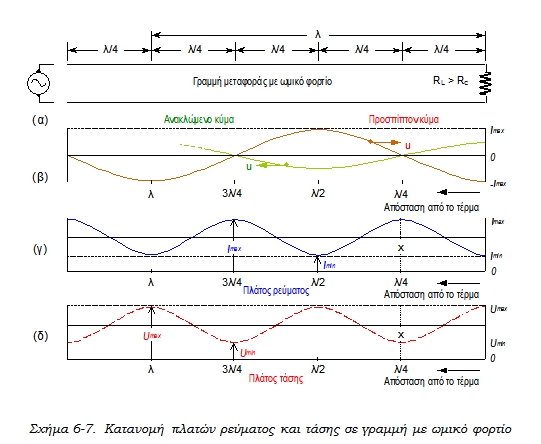
Όταν το ωμικό φορτίο δεν έχει τιμή ίση με τη χαρακτηριστική αντίσταση της γραμμής, τότε δεν μπορεί να απορροφήσει όλη την ενέργεια που έρχεται από την πηγή και ένα μέρος της το αντανακλά πίσω. Υπάρχουν λοιπόν προσπίπτοντα και ανακλώμενα κύματα πάνω στη γραμμή, που συνδυάζονται και προκαλούν αλλού ενισχύσεις και αλλού εξασθενήσεις της τάσης και του ρεύματος, όπως είδαμε να γίνεται και στο σχήμα 6-2. Εδώ όμως υπάρχει μια διαφορά. Επειδή μόνο ένα μέρος του κύματος ανακλάται, το ανακλώμενο κύμα έχει μικρότερο πλάτος από το προσπίπτον. Έτσι, όταν τα δύο κύματα συνδυάζονται, στα σημεία εξασθένησης δεν έχουμε μηδενισμό του πλάτους, αλλά απλώς μια ελάχιστη τιμή (σχήμα 6-7). Κατά μήκος της γραμμής υπάρχει ένας συνδυασμός από στάσιμα και τρέχοντα κύματα, που ονομάζονται μικτά κύματα.
Αν η αντίσταση φορτίου RL είναι μεγαλύτερη από τη χαρακτηριστική αντίσταση Rc της γραμμής, τότε στο τέρμα της γραμμής εμφανίζεται μέγιστο τάσης και ελάχιστο ρεύματος, όπως στο σχήμα 6-7. Αν η αντίσταση φορτίου είναι μικρότερη από τη χαρακτηριστική αντίσταση της γραμμής, τότε στο τέρμα της γραμμής εμφανίζεται μέγιστο ρεύματος και ελάχιστο τάσης. Τέλος, αν η αντίσταση φορτίου είναι ίση με τη χαρακτηριστική αντίσταση της γραμμής, τότε δεν υπάρχουν στη γραμμή μέγιστα και ελάχιστα, αλλά σε όλα τα σημεία της τα τρέχοντα κύματα έχουν σταθερό πλάτος. Μια συνοπτική απεικόνιση των κατανομών τάσης για διάφορες τιμές φορτίου φαίνεται στο σχήμα 6-8. Οι κατανομές ρεύματος είναι παρόμοιες, αλλά μετατοπισμένες κατά λ/4.
Αν η αντίσταση φορτίου, εκτός από καθαρά ωμικό έχει και χωρητικό ή επαγωγικό μέρος, τότε οπωσδήποτε ένα μέρος της ενέργειας του κύματος επιστρέφει στην πηγή και έτσι εμφανίζονται μικτά κύματα στη γραμμή μεταφοράς. Αν πάλι η αντίσταση φορτίου είναι καθαρά επαγωγική ή χωρητική, επειδή αυτές οι αντιστάσεις δεν καταναλώνουν ηλεκτρική ενέργεια, όλη η ενέργεια της πηγής επιστρέφει πίσω. Σ' αυτή την περίπτωση έχουμε πάντοτε δημιουργία στάσιμων κυμάτων στη γραμμή.
Η εμφάνιση στάσιμων ή μικτών κυμάτων πάνω σε μια γραμμή μεταφοράς είναι ιδιαίτερα ανεπιθύμητη κατάσταση, γιατί σημαίνει ότι ένα μέρος ή και όλη η ισχύς της πηγής δεν αποδίδεται στο φορτίο, αλλά επιστρέφει πίσω. Μπορούμε να διορθώσουμε αυτή την κατάσταση λαμβάνοντας μέτρα, που θα εξετάσουμε στην επόμενη παράγραφο. Προηγουμένως όμως θα πρέπει να διαπιστώσουμε την ύπαρξη του προβλήματος και για το σκοπό αυτό χρησιμοποιούμε κάποιο μέγεθος, που ονομάζεται λόγος στάσιμων κυμάτων (standing wave ratio ή SWR). Ο λόγος στάσιμων κυμάτων ορίζεται από τη σχέση:
SWR=Umax / Umin = Imax / Imin (6.2)
όπου Umax, Umin, Imax και Imin είναι οι μέγιστες και οι ελάχιστες τιμές τάσης και ρεύματος, όπως φαίνονται στο σχήμα 6-10.
Για τη μέτρηση του SWR υπάρχουν ειδικά όργανα, που ονομάζονται γέφυρες στάσιμων κυμάτων. Οι γέφυρες στάσιμων κυμάτων συνδέονται μεταξύ της πηγής και της γραμμής μεταφοράς και απεικονίζουν το λόγο στάσιμων κυμάτων απ' ευθείας πάνω σε μια κλίμακα μέτρησης. Η ιδανική και μικρότερη τιμή του SWR είναι ίση με 1. Η τιμή αυτή εμφανίζεται σε γραμμές όπου δεν υπάρχει ανακλώμενο κύμα, όπως στο σχήμα 6-11(α), οπότε τα μέγιστα και τα ελάχιστα έχουν το ίδιο πλάτος. Η μεγαλύτερη τιμή του SWR είναι ίση με άπειρο και εμφανίζεται στις ανοιχτές και τις βραχυκυκλωμένες γραμμές όπου τα ελάχιστα του πλάτους είναι ίσα με το μηδέν (σχήμα 6-8(β) και 6-8(δ)). Όταν SWR =1.5, η ανακλώμενη ισχύς είναι περίπου το 4% της προσπίπτουσας. Για SWR <2, το ποσοστό αυτό είναι λιγότερο από 10%. Για μεγαλύτερες τιμές του SWR, το ποσοστό της ανακλώμενης ισχύος αυξάνεται δραματικά. Στην πράξη τιμές του SWR μεταξύ 1.5 και 1.2 θεωρούνται πολύ καλές έως άριστες.
6.1.5 Προσαρμογή
Προσαρμογή ονομάζεται η εξασφάλιση των συνθηκών που επιτρέπουν τη μεταφορά της μέγιστης δυνατής ισχύος από μια πηγή σ' ένα φορτίο. Στην περίπτωση των γραμμών μεταφοράς η τέλεια προσαρμογή επιτυγχάνεται μόνο, όταν ταυτόχρονα η αντίσταση εξόδου της πηγής είναι ίση με τη χαρακτηριστική αντίσταση της γραμμής και η χαρακτηριστική αντίσταση της γραμμής είναι ίση με την αντίσταση φορτίου.
Τα κυριότερα πλεονεκτήματα μιας τέτοιας προσαρμογής είναι τα εξής:
- Το φορτίο τροφοδοτείται με τη μέγιστη ισχύ που μπορεί να δώσει η πηγή.
- Η μεταφορά της μέγιστης δυνατής ισχύος επιτυγχάνεται ανεξάρτητα από το μήκος της γραμμής και από τη συχνότητα.
- Οι απώλειες ισχύος και ο κίνδυνος καταστροφής του μονωτικού της γραμμής από τοπικές ανυψώσεις της τάσης μειώνονται στο ελάχιστο δυνατό.
Η τέλεια όμως προσαρμογή δεν είναι πάντοτε δυνατή. Πολλές φορές είμαστε υποχρεωμένοι να χρησιμοποιήσουμε μια πηγή με αντίσταση εξόδου διαφορετική από την αντίσταση φορτίου και τότε οι δύο αυτές αντιστάσεις δεν μπορούν να είναι ταυτόχρονα ίσες με τη χαρακτηριστική αντίσταση της γραμμής. Το μόνο που μπορούμε να κάνουμε σ' αυτή την περίπτωση είναι να εφαρμόσουμε μια μέση λύση, που ονομάζεται μερική προσαρμογή.
Στηριζόμαστε σε μια ιδιότητα των γραμμών μεταφοράς, που μπορούμε να τη δούμε στο σχήμα 6-8. Στο τέρμα της γραμμής το ρεύμα είναι μικρό και η τάση μεγάλη. Αυτό σημαίνει ότι η αντίσταση εκεί είναι μεγάλη. Αντίθετα, στο σημείο χ που απέχει λ/4 από το τέρμα, το ρεύμα είναι μεγάλο και η τάση μικρή, δηλαδή η αντίσταση εκεί είναι μικρή. Αυτό σημαίνει ότι ένα τμήμα γραμμής μεταφοράς με μικτά κύματα κατά μήκος της μπορεί να λειτουργήσει σαν μετασχηματιστής και να μετασχηματίσει μια τιμή αντίστασης σε μια άλλη.
Αν θέλουμε να προσαρμόσουμε μια πηγή με αντίσταση εξόδου Ro σε φορτίο με αντίσταση RL διαφορετική της Ro, συνδέουμε στα άκρα του φορτίου ένα κομμάτι γραμμής μεταφοράς με μήκος λ/4 και χαρακτηριστική αντίσταση:
Την υπόλοιπη απόσταση μέχρι την πηγή την καλύπτουμε με γραμμή μεταφοράς, που έχει χαρακτηριστική αντίσταση ίδια με την αντίσταση εξόδου της πηγής (σχήμα 6-9).
Το τμήμα λ/4 μετασχηματίζει την αντίσταση RL και την εμφανίζει στα σημεία Α, Β ίση με την Ro. Έτσι, σε όλο το μήκος της γραμμής από την πηγή μέχρι τα Α, Β η προσαρμογή είναι τέλεια και δεν υπάρχουν στάσιμα κύματα. Μεταξύ των Α, Β και του φορτίου δεν υπάρχει προσαρμογή και εμφανίζονται μικτά κύματα. Αυτό όμως δεν μπορούμε να το αποφύγουμε και επιπλέον δεν μας ενοχλεί πολύ, γιατί το κομμάτι αυτό έχει συνήθως μικρό μήκος.