Θεωρούμε ένα τετράγωνο ΟΑΓΔ. Αν το τμήμα ΔΓ αρχίσει να κινείται προς τα κάτω με σταθερή ταχύτητα μένοντας παράλληλο προς το ΟΑ και ταυτόχρονα το ΟΔ να περιστρέφεται γύρω από το Ο με σταθερή ταχύτητα επίσης και τα δύο τμήματα φθάσουν ταυτόχρονα στην ΟΑ, τότε τα σημεία τομής τους θα γράψουν μία καμπύλη. Η καμπύλη αυτή είναι η τετραγωνίζουσα .(κάντε κλικ στο διπλανό τετράγωνο να τη δείτε) .
Παρακάτω θα δούμε πως με χρήση της τετραγωνίζουσας γίνεται η τριχοτόμηση της γωνίας.
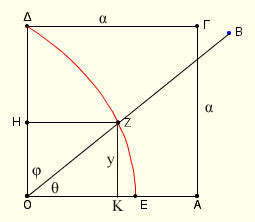
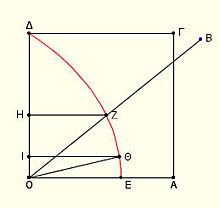
Στο διπλανό σχήμα έχουμε ένα τετράγωνο ΟΑΓΔ.
Θεωρούμε ότι το τμήμα ΔΓ κινείται με σταθερή ταχύτητα υ και το ΟΔ περιστρέφεται γύρω από το Ο με σταθερή γωνιακή ταχύτητα ω. Αν θεωρήσουμε ότι μετά από χρόνο t , το ΔΓ είναι στη θέση HΖ δηλ έχει
διαγράψει τη απόσταση ΔΗ , και το ΟΔ έχει γράψει τη γωνία φ θα είναι τότε ΔΗ=υt και φ=ωt. Θα είναι τότε:
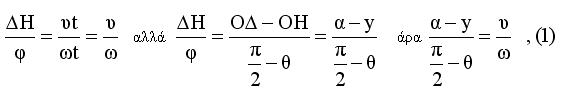
Αν Τ είναι ο συνολικός χρόνος μέχρι τα τμήματα να φθάσουν στη θέση ΟΑ θα έχουμε
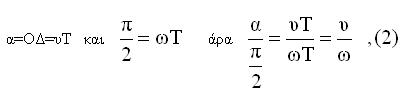
Από τις (1) και (2) έχουμε
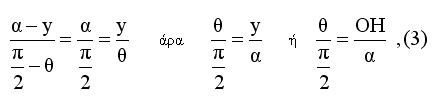
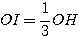
Πράγματι σύμφωνα με την παραπάνω σχέση (3) θα είναι
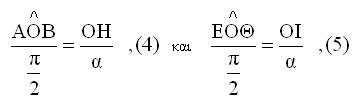Διαιρώντας τις (4),(5) κατά μέλη έχουμε
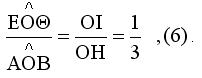Δηλ η γωνία ΕΟΘ είναι το ένα τρίτο της ΑΟΒ
Προφανώς η τριχοτόμηση της γωνίας με αυτό το τρόπο προϋποθέτει τη κατασκευή της τετραγωνίζουσας, πράγμα που δεν μπορεί να γίνει με κανόνα και διαβήτη. Μπορούμε να βρούμε όσα σημεία της τετραγωνίζουσας θέλουμε δεν μπορούμε όμως να τη σχεδιάσουμε πλήρως ειδικά το σημείο Ε, όπου τα τμήματα είναι παράλληλα προσδιορίζεται μόνο με όρια .Στο παρακάτω applet μπορείτε να παρακολουθήσετε τη παραπάνω κατασκευή. Πατήστε το πλήκτρο " Start".
Τελευταία ενημέρωση :
