Τριχοτόμηση γωνίας -Η δεύτερη λύση του Πάππου

Τριχοτόμηση Γωνίας -Η δεύτερη λύση του Πάππου

Ο Πάππος στο έργο του "Μαθηματική συναγωγή" έδωσε δύο λύσεις στο πρόβλημα της τριχοτόμησης μιας γωνίας.
Η δεύτερη από αυτές, στηρίζεται σε μία ειδική υπερβολή, που παρουσιάζουμε αρχικά.

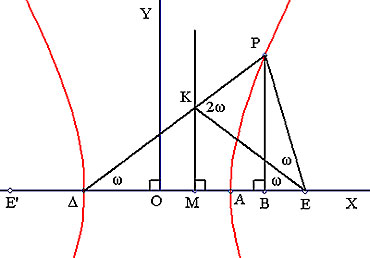
Έστω δύο σταθερά σημεία Ε και Δ ,θα βρούμε τον γεωμετρικό τόπο των σημείων Ρ του επιπέδου για τα οποία ισχύει η σχέση $hat(PEDelta)=2hat(PDeltaE)$ (1)

Έστω Ρ ένα τέτοιο σημείο και Μ το μέσο του ΕΔ, φέρουμε την κάθετη στην ΕΔ στο Μ η οποία τέμνει την ΡΔ στο Κ, τότε $hat(KDeltaE)=hat(KEDelta)$

Άρα η ΚΕ θα είναι διχοτόμος της γωνίας ΡΕΔ και η γωνία ΡΚΕ θα είναι 2ω ως εξωτερική του τριγώνου ΚΔΕ. Επειδή η ΚΕ είναι διχοτόμος της γωνίας ΡΕΔ ισχύει $(EDelta)/(EP)=(KDelta)/(KP)$ (2)
Φέρουμε την ΡΒ κάθετη στην ΔΕ άρα ΚΜ//ΡΒ και θα ισχύει $(KDelta)/(KP)=(DeltaM)/(MB)$ (3)

Από τις (2) και (3) προκύπτει $(EDelta)/(EP)=(DeltaM)/(MB)$ ή $(EDelta)/(DeltaM)=(EP)/(MB)$ και επειδή είναι EΔ=2ΔΜ θα είναι $(EP)/(MB)=2$ (4)

Το ΜΒ όμως είναι ίσο με την απόσταση του Ρ από την ΚΜ ,άρα από τη σχέση (4) προκύπτει ότι το Ρ θα βρίσκεται σε μία υπερβολή με εκκεντρότητα ε=2, η οποία θα έχει εστία το σημείο Ε και διευθετούσα την ΚΜ . Αν πάρουμε ένα σημείο Α πάνω στο ΔΕ ώστε ΑΕ=2ΜΑ, τότε το Α θα είναι σημείο της υπερβολής όπως επίσης και το Δ αφού ΔΕ=2ΔΜ . Αν θεωρήσουμε ένα σύστημα συντεταγμένων του οποίου ο άξονας ΟΧ να ταυτίζεται με την ΜΕ τότε τα σημεία Α και Δ θα είναι οι κορυφές της υπερβολής και το μέσο Ο του ΔΑ το κέντρο του συστήματος.

Θέτουμε α=ΟΑ και επειδή ε=2 από τη σχέση $epsilon=gamma/alpha$ προκύπτει $gamma=2alpha$ και η $gamma^2=alpha^2+beta^2$ δίνει $beta^2=3alpha^2$
άρα η υπερβολή έχει εξίσωση $x^2/alpha^2 - y^2/(3alpha^2) = 1$

Χρησιμοποιπώντας την παραπάνω υπερβολή, η τριχοτόμηση μιας γωνίας γίνεται όπως παρουσιάζεται στην παρακάτω εφαρμογή.

Απόδειξη:

Επειδή το σημείο Ρ ανήκει στην υπερβολή θα είναι $hat(PEDelta)=2hat(PDeltaE)$ .
Η γωνία $hat(PKΕ)$ είναι επίκεντρη και βαίνει στο ίδιο τόξο με την $hat(PDeltaΕ)$ άρα θα είναι $hat(PKΕ) = 2hat(PDeltaE) = hat(PEDelta)$ λόγω της προηγούμενης σχέσης.

Όμοια για την $hat(DeltaKP)$ θα είναι $hat(DeltaKP) = 2hat(PEDelta) = 2hat(PKE)$ άρα η γωνία $hat(PKΕ)$ θα είναι το ένα τρίτο της $hat(DeltaKΕ)$ .
Έτσι η γωνία $hat(ΒKG)$ τριχοτομήθηκε.

Βιβλιογραφία

Προηγούμενη Κεντρική σελίδα Επόμενη