

Ο Νικομήδης για να λύση το πρόβλημα της τριχοτόμησης της γωνίας και του τετραγωνισμού του κύβου επινόησε μια καμπύλη ,την κογχοειδή την οποία παρουσιάζουμε παρακάτω.
Ας πάρουμε μια ευθεία OX και ένα σημείο K σε απόσταση KK'=α από αυτήν .Θεωρούμε ένα σημείο Μ που κινείται πάνω στην OX
και πάνω στην KM παίρνουμε δύο σημεία και P,Λ εκατέρωθεν του Μ ώστε ΜΛ=MΠ=β. Καθώς το Μ κινείται πάνω στην ΟΧ ο γεωμετρικός τόπος των
P,Λ αποτελεί την κογχοειδή.
Το σημείο Κ λέγεται πόλος, η ευθεία ΟΧ βάση ή κανόνας και το μήκος β διάστημα .
Για να την κατασκευάσετε,κινείστε το Μ πάνω στην ΟΧ. Μπορείτε να αυξήσετε και το τμήμα β.
Η καμπύλη κατασκευάζεται με χρήση του ορισμού και όχι με χρήση εξίσωσης. Δηλ
κατά την κίνηση των P,Λ αποθηκεύουμε τις διαδοχικές τους θέσεις και ενώνουμε τα σημεία που προκύπτουν .Γι' αυτό απαιτείται προσεκτική κίνηση.
Παρακάτω παρουσιάζουμε τη λύση πουέδωσε ο Νικομήδης στο πρόβλημα της τριχοτόμησης της γωνίας, χρησιμοποιώντας την παραπάνω καμπύλη.

Νικομήδης, Έλληνας μαθηματικός του 2ου αι. .π.χ
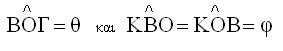 είναι ΚΒ=ΚΟ ως ακτίνες του κύκλου
είναι ΚΒ=ΚΟ ως ακτίνες του κύκλου
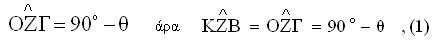
Επειδή το σημείο Β ανήκει στη κογχοειδή είναι ΒΖ=β=ΚΟ=ΚΒ αφού η κογχοειδή γράφτηκε με διάστημα β=ΚΟ άρα το τρίγωνο ΚΒΖ είναι ισοσκελές και έχουμε
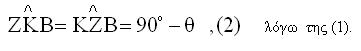
Από το ορθογώνιο τρίγωνο ΚΓΟ έχουμε
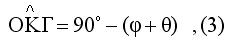
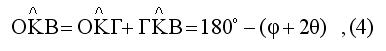
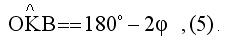 Από τις (4),(5) προκύπτει
Από τις (4),(5) προκύπτει
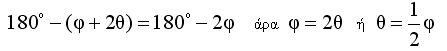
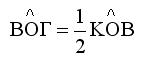 Έτσι η γωνία ΧΟΖ τριχοτομήθηκε .
Έτσι η γωνία ΧΟΖ τριχοτομήθηκε .