Διπλασιασμός του κύβου -Η λύση του Νικομήδη
Ο Νικομήδης για να λύση το πρόβλημα της τριχοτόμησης της γωνίας και του τετραγωνισμού του κύβου επινόησε μια καμπύλη,την κογχοειδή και κατασκεύασε ένα όργανο με το οποίο μπορεί να κατασκευασθεί
με συνεχή κίνηση. Την καμπύλη αυτή παρουσιάσαμε αναλυτικά την τριχοτόμηση της γωνίας, η λύση του Νικομήδη. Στο παρακάτω applet μπορείτε να την κατασκευάσετε κινώντας το σημείο Μ, με τον slider ορίζουμε τις ίσες αποστάσεις ΜΡ=ΜΛ.
Παρακάτω παρουσιάζουμε την λύση του προβλήματος του διπλασιασμού του κύβου με χρήση της παραπάνω καμπύλης.
Διαβάστε τις οδηγίες για την κατασκευή του σχήματος .
Όπως έχουμε αναφέρει ο Ιπποκράτης απέδειξε ότι αν κατασκευάσουμε δύο τμήματα x και y ώστε να ισχύει
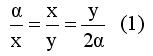 τότε το τμήμα x είναι το ζητούμενο
τότε το τμήμα x είναι το ζητούμενο
Θα αποδείξουμε ότι στη παραπάνω κατασκευή ισχύει
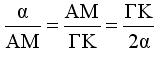
οπότε x = AM
Τα τρίγωνα ΑΜΔ και ΔΓΚ είναι όμοια άρα
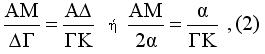
Είναι ΓΘ//ΗΖ άρα
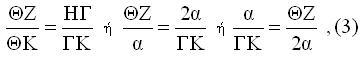
Από (2) και (3) έχουμε ΘΖ=ΑΜ και ΖΚ=ΖΘ+ΘΚ=ΑΜ+ΑΛ
Από το ΕΓΖ έχουμε
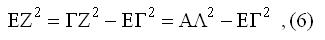
αφού ΓΖ=ΒΖ=ΑΛ
Από το ΖΕΚ έχουμε
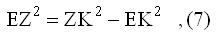
Από τις (4),(5),(6),(7) προκύπτει ότι
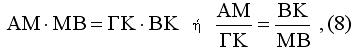
Τα τρίγωνα ΜΒΚ και ΔΓΚ είναι όμοια ,άρα
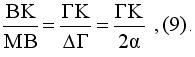
Από τις (8) και (9) προκύπτει
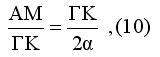
από την (2) προκύπτει
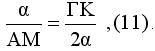
Από τις (10) και (11) προκύπτει
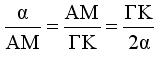
άρα x = AM


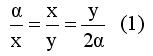 τότε το τμήμα x είναι το ζητούμενο
τότε το τμήμα x είναι το ζητούμενο
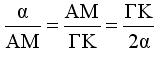 οπότε x = AM
οπότε x = AM
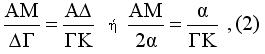
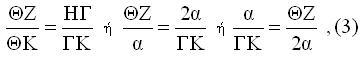

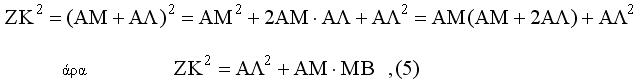
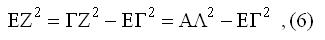 αφού ΓΖ=ΒΖ=ΑΛ
αφού ΓΖ=ΒΖ=ΑΛ
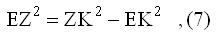
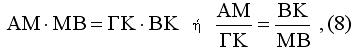
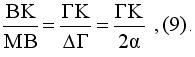
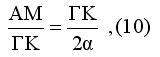
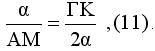
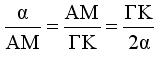 άρα x = AM
άρα x = AM