Οι δυνάμεις των σημείων Μ και Κ ως προς τον κύκλο μας δίνουν τις σχέσεις
ΜΑ·ΜΟ=ΜΒ·ΜΔ και ΚΓ·ΚΟ=ΚΔ·ΚΒ (1).
Τα τμήματα ΜΒ και ΚΔ είναι ίσα (
απόδειξη
) άρα και τα ΜΔ και ΚΒ έτσι τα δεύτερα μέλη των (1) είναι ίσα, άρα και τα πρώτα δηλ ΜΑ·ΜΟ = ΚΓ·ΚΟ άρα
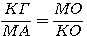(2).
Τα τρίγωνα ΚΓΒ και ΚΟΜ είναι όμοια, άρα
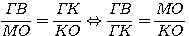(3)
Επίσης τα τρίγωνα ΜΑΒ και ΜΟΚ είναι όμοια, άρα
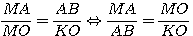(4)
Τα δεύτερα μέλη των (2),(3),(4) είναι ίσα, άρα
.
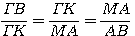Θέτουμε ΓΚ=y ,ΜΑ=x ,είναι και ΓΒ=2α ,ΑΒ=α και η προηγούμενη σχέση δίνει
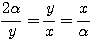
Δηλ καταλήξαμε στην αναλογία του Ιπποκράτη και συνεπώς το ζητούμενο τμήμα είναι το ΜΑ
Τελευταία ενημέρωση :
