

Η κισσοειδής προκύπτει με τον εξής τρόπο.
Στο άκρο μιας διαμέτρου ΟΑ ενός κύκλου φέρουμε μια κάθετο, πάνω σ' αυτήν παίρνουμε ένα σημείο Β και φέρουμε την ΟΒ η οποία τέμνει τον κύκλο στο Γ.
Πάνω στην ΟΒ ορίζουμε το σημείο Δ ώστε ΒΔ=ΟΓ.
Καθώς το Β κινείται πάνω στην κάθετο το σημείο Δ γράφει την κισσοειδή καμπύλη. Κινείστε σιγά-σιγά με το ποντίκι το Β να σχηματιστεί. Η κισσοειδής έχει μια σπουδαια ιδιότητα την οποία θα δούμε παρακάτω.
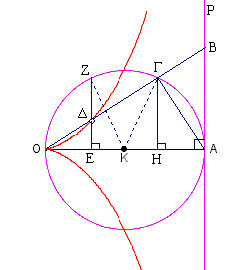
Έστω Δ ένα σημείο της κισσοειδούς, φέρουμε την ΟΔ που τέμνει τον κύκλο στο Γ και την ΑΡ στο Β. Φέρουμε τις ΓΗ και ΔΕ κάθετες στην ΟΑ. Επειδή το Δ είναι σημείο της κισσοειδούς είναι ΟΔ=ΒΓ και λόγω των παραλλήλων ΔΕ//ΓΗ//ΒΑ θα είναι ΟΕ=ΑΗ άρα, ΕΚ=ΚΗ και ΟΗ=ΑΕ
Τα τρίγωνα ΟΔΕ και ΟΓΗ είναι όμοια άρα ισχύει
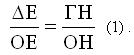
Το τμήμα ΓΗ είναι ύψος στο ορθογώνιο τρίγωνο ΟΓΑ άρα,
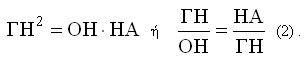
Από τις (1) και (2) προκύπτει
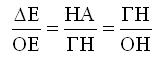
και επειδή ΟΕ
= ΗΑ, ΟΗ=ΑΕ και ΓΗ= ΖΕ (από τα ίσα τρίγωνα ΖΕΚ και ΓΚΗ) η παραπάνω γράφεται
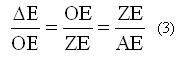
Η (3) είναι η ιδιότητα της κισσοειδούς και σημαίνει ότι, τα τμήματα ΟΕ και ΖΕ βρίσκονται σε συνεχή αναλογία με τα ΔΕ και ΑΕ.
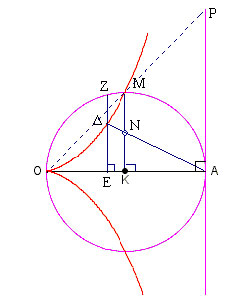
Για να λύσουμε το πρόβλημα του διπλασιασμού του κύβου θεωρούμε ένα τυχαίο κύκλο, γράφουμε την κισσοειδή, παίρνουμε το μέσο Μ του τόξου ΟΑ και φέρουμε την ΜΚ η οποία θα είναι κάθετη στην ΟΑ και παράλληλη στην ΑΡ .Από το τρίγωνο ΟΑΡ προκύπτει ότι ΟΜ=ΡΜ άρα το Μ είναι σημείο της κισσοειδούς .
Παίρνουμε ένα σημείο Ν της ΚΜ ώστε
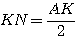 φέρουμε την ΑΝ η οποία τέμνει την κισσοειδή στο Δ και την ΔΕ κάθετη στην ΟΑ.
φέρουμε την ΑΝ η οποία τέμνει την κισσοειδή στο Δ και την ΔΕ κάθετη στην ΟΑ.
Τα τρίγωνα ΑΔΕ και ΑΚΝ είναι όμοια, άρα
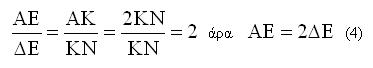
Το σημείο Δ ανήκει στην κισσοειδή άρα θα ισχύει η σχέση (3) δηλ,
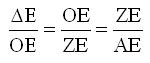
Θέτουμε ΔΕ=β ,ΟΕ=
x ,
ZE =
y και λόγω της (4) η παραπάνω γράφεται
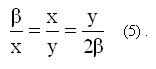
Η (5) είναι η σχέση του Ιπποκράτη και σημαίνει ότι, αν ο κύβος που θέλουμε να διπλασιάσουμε έχει πλευρά β τότε η πλευρά του διπλάσιου κύβου είναι η x = OE. Αν τώρα ο κύβος μας έχει πλευρά α τότε η πλευρά του διπλάσιου κύβου θα προκύψει από την σχέση
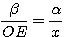 δηλ θα κατασκευαστεί ως τετάρτη ανάλογος των β, ΟΕ και α.
δηλ θα κατασκευαστεί ως τετάρτη ανάλογος των β, ΟΕ και α.
Αν πάρουμε
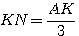 τότε η παραπάνω διαδικασία θα δώσει,
τότε η παραπάνω διαδικασία θα δώσει,
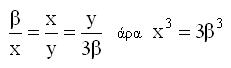
δηλ η x = OE θα είναι η πλευρά του τριπλάσιου κύβου ,όμοια μπορούμε να βρούμε την πλευρά του τετραπλάσιου ,πενταπλάσιου κ.τ.λ κύβου .
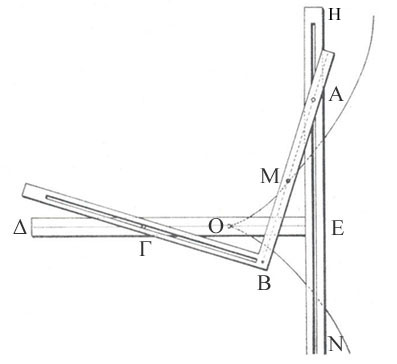
Το παραπάνω όργανο προσομοιώνουμε με την παρακάτω εφαρμογή. Διαβάστε τις οδηγίες για την κατασκευή του .