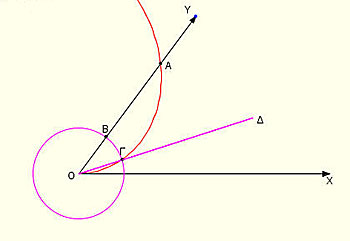
Έστω ΧΟΥ η γωνία που θέλουμε να τριχοτομήσουμε. Γράφουμε την έλικα με κορυφή το Ο και αρχική πλευρά την ΟΧ(κόκκινη γραμμή) και βρίσκουμε το σημείο Α που τέμνει την πλευρά ΟΥ της γωνίας. Από τον ορισμό της έλικας προκύπτει ότι: καθώς η ΟΧ διαγράφει την γωνία ΧΟΥ, το σημείο Ο κινούμενο πάνω στην ΟΧ, γράφει το τμήμα ΟΑ.
Χωρίζουμε το ΟΑ σε τρία ίσα μέρη και ορίζουμε το σημείο Β ώστε
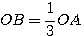, γράφουμε τον κύκλο (Ο,ΟΒ) ο οποίος τέμνει την έλικα στο σημείο Γ και φέρουμε την ΟΓ.
Από τον ορισμό της έλικας προκύπτει ότι: καθώς η ΟΧ διαγράφει την γωνία ΧΟΓ, το σημείο Ο κινούμενο πάνω στην ΟΧ, γράφει το τμήμα ΟΓ και επειδή το ΟΓ είναι το ένα τρίτο του ΟΑ (σαν ίσο προς το ΟΒ) η γωνία ΧΟΓ θα είναι το ένα τρίτο της ΧΟΥ. Είναι φανερό ότι αν χωρίσουμε το τμήμα ΟΑ σε ν ίσα μέρη και ακολουθήσουμε την ίδια διαδικασία θα χωρίσουμε και την γωνία σε ν ίσα μέρη και θα βρούμε το ένα νιοστό της .
Η παραπάνω διαδικασία φαίνεται βήμα -βήμα στην παρακάτω εφαρμογή. Στη πρώτη καρτέλα παρουσιάζουμε την έλικα με πολλές επιλογές σχεδίασης και στη δεύτερη την τριχοτόμηση της γωνίας.
Τελευταία ενημέρωση :
